输出分组_Learnable Group Convolutions:可以学习的分组卷积

这篇文章里我们介绍两篇论文[1]和[2]，都是关于可以学习的分组卷积（learnable group convolution）。

传统的卷积操作中每一个输出的 channel 都与输入的每一个 channel 相连接，channels 之间是一个稠密连接。Group Convolution 中输入和输出的 channels 被分为

个 组（groups），每个组的输出 channels 只和对应组内的输入 channels 相连接，与其它 channels 无关。

图1：regular convolution 和 group convolution。

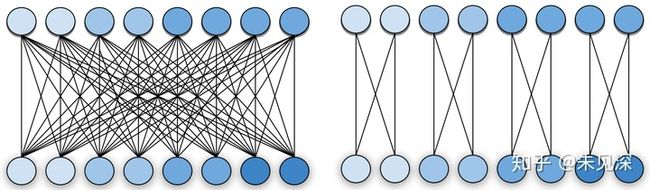
图1 中左边为regular convolution，输出的每个 channel （下方圆圈）和输入的每一个 channel （上方的圆圈）都有连接。右边是 Group Convolution，输入输出 channels 被分为

个 groups，输出 channels 只与组内的输入 channels 建立连接。上图来自[1]

与 regular convolution 相比， 在同样的输入输出 channels 的情况下，group convolution的参数会减小

倍。以一个输入输出都是64个 channels 的

卷积为例，regular conv 的参数是

,而

的 group conv 的参数则为

。

但是在 group conv 中，一共分多少个 groups，每个 group 分别有多少 channels，哪些 channels 在同一个 group，这些参数都是事先预设的，需要手工设计。

---

下面我们先讲论文[2]的方法，这篇论文解决了“每个 group 分别有多少个 channels”以及“哪些 channels 在同一个 group”这两个问题。

假设一个 conv 层的输入输出 channels 个数分别是

和

，这些 channels 被分成

个 groups。在前面已经说了，这篇论文解决了“每个 group 分别有多少个 channels”以及“哪些 channels 在同一个 group”这两个问题，因此“每个 conv 层分成几个 groups”仍然是预设的。

一个 group conv 的结构很容易用两个 shape 分别是

和

的二值矩阵

和

表示，前提是要保证

这两个矩阵的每一行只有一个非零元素。因为每个（输入或者是输出）channel 只能属于一个 group。

如果能在每个卷积层中插入

和

作为参数，并在训练的时候自动更新这两个参数，就能 end-to-end 的学到 group conv 结构了。

但是有一个问题，这样二值化的参数放在网络中是不可导的，因此不能在网络中自动优化。在文章中作者先初始化一个随机的实数矩阵

和

，在训练过程中将它们按行取softmax，这样可以尽可能保证

每一行只有一个非零元素。经过训练之后再根据 S 和 T 对输入输出 channels 进行分组，得到 group conv 化的网络。

总结一下：[2]这篇文章提出用两个参数矩阵 S 和 T 来分别参数化输入、输出 channels 的分组情况。并在训练过程中自动优化这两个参数，于是得到自动学习到的 group conv，每个 group 中有几个 channels，有哪些 channels 都由模型自动学习到。

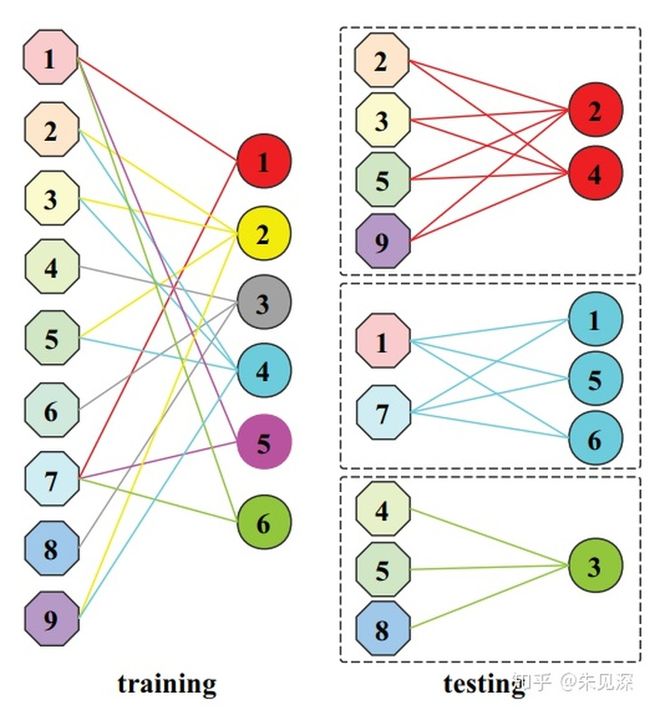
这种方法我个人觉得有一个缺点，就是学到的分组并不是很“结构化”，每个组的输入、输出 channels 都不一定相同，不方便放到目前各框架实现的 group conv 中直接使用。

图2：论文[2]得到的group convolution并不是结构化的，每个group中的channels数并不一定相等，不容易应用到现有框架中。

---

下面介绍第二篇论文[1]，来自 ICCV2019。

这篇论文解决 “一个 conv 层应该分为几组”和“哪几个 channels 放在同一个组”这两个问题。因此 channels 仍然是均匀的分配到每一个 groups中。

类似的，这篇文章用一个 binary 矩阵 U 来表示一个卷积层中输入输出 channels 之间的连接。

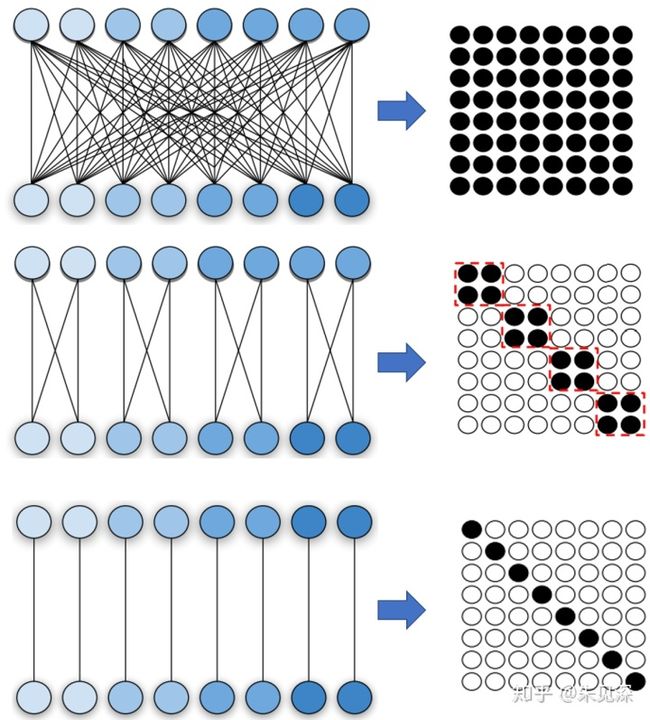
下图列举了几种 conv 和其对应的矩阵U，所有图片都来自[1]。

图3：几种不同的卷积层连接和对应的参数矩阵 U。上：regular convolution，输入输出 channels 之间稠密连接；中：group convolution，输入、输出channels 被分为若干个 gorups，每个group中的 channels只与同group的channels连接；下：depth-wise convolution，groups数目等于输入、输出 channels个数

那么和[2]类似的，我们只需要在训练中把 U 当做一个参数去学习，就能得到一个卷积层的分组情况。

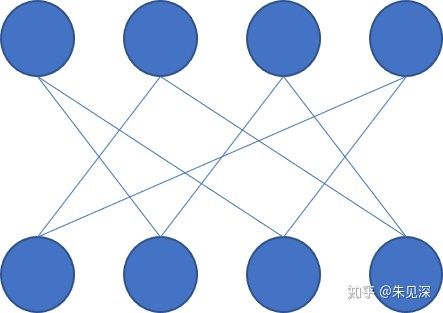
问题的关键是，不是每一个二值矩阵都可以表示一个 group conv 的分组情况。我们可以很轻易的举一个反例，考虑以下连接：

图4：一种不可以被表示为 group conv 的连接。

与 图2 的第二种情况类似，图4 中的每个输入 channel 也是只与 两个输出 channels 相连接，但是显然上图中的连接不能表示为 group conv。

那么矩阵 U 究竟要满足什么样的条件才能使得所表示的连接是一个分组卷积呢？

这个问题很重要，我们只有在满足约束的条件下优化 U，才能得到分组卷积的结构。

在[1]中，作者将矩阵 U 表示为若干个

个矩阵的[Kronecker乘积](

https:// en.wikipedia.org/wiki/K ronecker_product )的形式。对于Kronecker乘积，大家可以去看维基百科 https:// en.wikipedia.org/wiki/K ronecker_product ，下面用一个简单的例子来解释它。

上图是两个2x2的矩阵的 Kronecker 乘积，图片来自维基百科。

结论1：如果一个矩阵 U 是多个

矩阵的 Kronecker 乘积，那么 U 所表示的连接一定是分组卷积。

这个结论作者好像并没有在论文中证明，我们不妨把图3 中几种分组连接的参数矩阵分别作 Kronecker 分解：

图5：几种典型的group conv以及对用的 Kronecker 分解。上：g=1;中g=4；下g=8.

以上几种典型的分组卷积连接（regular conv可以认为是g=1的分组卷积）对应的 U 均可以被 Kronecker 分解。

因此我们只需要将

(

是channels个数)个

的矩阵

作为参数优化，最终用

确定分组结构，即可得到end-to-end学习到的分组卷积。

我觉得“将 group conv参数矩阵 U 表示为若干个矩阵的 Kronecker 分解”是一个很巧妙的设计。但是“矩阵 U 可以表示为若干个2x2矩阵的 Kronecker 乘积”和 “矩阵 U 可以参数化一个 group conv 的结构信息”这两者并不是充要的，前者只是充分条件，并不是必要的。换句话说，可以被 Kronecker 分解的矩阵 U 可能无法表示所有的 group conv 连接，也就是说这种方法对 group conv 连接的搜索空间被极大缩小了。

下图是举例了一种无法被 Kronecker 分解的 group conv：

图6：一种无法被 Kronecker 分解的 group conv。

---

[1]和[2]都涉及到一些如何将参数矩阵二值化（因为只有binary的矩阵U[1]以及S，T[2]才能表示group结构），如果将二值参数作为可导参数放到模型进行训练等细节问题。这里只介绍这两个论文的主要 idea，如果对细节感兴趣大家可以参考对应的文献。

全文完。感谢阅读！

---

[1] Zhaoyang Zhang, Jingyu Li, Wenqi Shao, Zhanglin Peng, Ruimao Zhang, Xiaogang Wang, Ping Luo. "Differentiable Learning-to-Group Channels via Groupable Convolutional Neural Networks" ICCV2019

[2] Xijun Wang; Meina Kan; Shiguang Shan; Xilin Chen "Fully Learnable Group Convolution for Acceleration of Deep Neural Networks" CVPR2019