《动手学深度学习》参考答案(第二版)-第二章

  最近在学习《动手学深度学习》，结合百度和课后的大家的讨论(侵删)，整理出这一份可能并不完全正确的参考答案(菜鸡的做题记录)，因为个人水平有限，有错误的地方欢迎在 公众号 联系我，后面我对错误进行更正时候，会在文章末尾鸣谢，在这里先感谢大家了。
  因为 上传图片有点模糊 ，在我的 公众号 中会有 清晰的pdf版本 给到大家，pdf中 代码 可以直接复制实践 ，欢迎大家关注我的 公众号 ，发送神秘代码：d2l2，即可获得本章的pdf版本。(求大佬们关注下吧，公众号关注者人丁稀少，嘤嘤嘤)

  求求关注下我的CSDN、知乎吧，后面会继续更新答案的，然后还有最近读的一些文章的里面一些创新点和自己的想法都会整理出来的。(求大佬们关注下吧，嘤嘤嘤)

2.预备知识

2.1 数据操作

1.运行本节中的代码。将本节中的条件语句X == Y更改为X < Y或X > Y，然后看看你可以得到什么样的张量。

import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X > Y

tensor([[False, False, False, False],
        [ True,  True,  True,  True],
        [ True,  True,  True,  True]])

X < Y

tensor([[ True, False,  True, False],
        [False, False, False, False],
        [False, False, False, False]])

2.用其他形状（例如三维张量）替换广播机制中按元素操作的两个张量。结果是否与预期相同？

结论是相同的，都在广播机制下进行了运算

import torch
a = torch.arange(3).reshape((1, 3, 1))
b = torch.arange(4).reshape((2, 1, 2))
a, b

(tensor([[[0],
          [1],
          [2]]]), 
 tensor([[[0, 1]],
         [[2, 3]]]))

a + b

tensor([[[0, 1],
         [1, 2],
         [2, 3]],

        [[2, 3],
         [3, 4],
         [4, 5]]])

(a + b).size()

torch.Size([2, 3, 2])

2.2 数据预处理

1.删除缺失值最多的列。

key_dict = data.isna().sum().to_dict()
max_key = max(num_dict, key=num_dict.get)
del data[max_key]

2.将预处理后的数据集转换为张量格式。

import torch
inputs, outputs = data.iloc[:, 0], data.iloc[:, 1]
X, Y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, Y

tensor([nan, 2., 4., nan], dtype=torch.float64),
tensor([127500, 106000, 178100, 140000])

2.3 线性代数

1.证明一个矩阵A的转置的转置是A，即(A⊤)⊤=A。
$$设B=A^T,C=B^T$$

$$那么根据转置定义,b_{ji}=a_{ij},c_{ij}=b_{ji}$$

$$即c_{ij}=a_{ij},即C=B^T=(A^T{)}^T=A,得证(A^T{)}^T=A$$

2.给出两个矩阵A和B，证明“它们转置的和”等于“它们和的转置”，即A⊤+B⊤=(A+B)⊤。
$$设C=A+B$$

$$由c_{ij}=a_{ij}+b_{ij},得c_{ji}=a_{ji}+b_{ji}$$

$$即C^T=A^T+B^T,又C=A+B,即(A+B{)}^T=A^T+B^T$$

3.给定任意方阵A，A+A⊤总是对称的吗?为什么?
$$设B=A+A^T,则b_{ij}=a_{ij}+a_{ji}$$

$$则b_{ji}=a_{ji}+a_{ij}=a_{ij}+a_{ji}=b_{ij},即B为对称阵,即A+A^T为对称阵$$

4.我们在本节中定义了形状(2,3,4)的张量X。len(X)的输出结果是什么？

len(x) = 2

5.对于任意形状的张量X,len(X)是否总是对应于X特定轴的长度?这个轴是什么?

总是对应axis=0这个轴

6.运行A/A.sum(axis=1)，看看会发生什么。你能分析原因吗？

运行运行A/A.sum(axis=1)是会报错的，是广播机制的原因，但是我们可以顺利运行A/A.sum(axis=1, keepdim=True)，我们可以来做个实验，实验中我们可以看到沿着不同的轴进行计算会有不同结果且写的方法不同，在axis≠0时一般需要加上keepdim=True

import torch
A = torch.ones((3, 4))
B = A/A.sum(axis=1, keepdim=True)
C = A/A.sum(axis=0)
B, C

tensor([[0.2500, 0.2500, 0.2500, 0.2500],
        [0.2500, 0.2500, 0.2500, 0.2500],
        [0.2500, 0.2500, 0.2500, 0.2500]]),
tensor([[0.3333, 0.3333, 0.3333, 0.3333],
        [0.3333, 0.3333, 0.3333, 0.3333],
        [0.3333, 0.3333, 0.3333, 0.3333]])

7.考虑一个具有形状(2,3,4)的张量，在轴0、1、2上的求和输出是什么形状?

形状分别为[3, 4]，[2, 4]，[2, 3]

实验如下

import torch
A = torch.ones((2, 3, 4))
B = A.sum(axis=0)
C = A.sum(axis=1)
D = A.sum(axis=2)
B.size(), C.size(), D.size()

(torch.Size([3, 4]), torch.Size([2, 4]), torch.Size([2, 3]))

8.为linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么?

先查看下api：

torch.linalg.norm(input, ord=None, dim=None, keepdim=False, *, out=None, dtype=None)

参数	说明
默认	二范数
ord=2	二范数
ord=1	一范数
ord=torch.inf	无穷范数

代码实验：

import torch
A = torch.ones((3,4))
torch.linalg.norm(A)

tensor(3.4641)

2.4 微积分

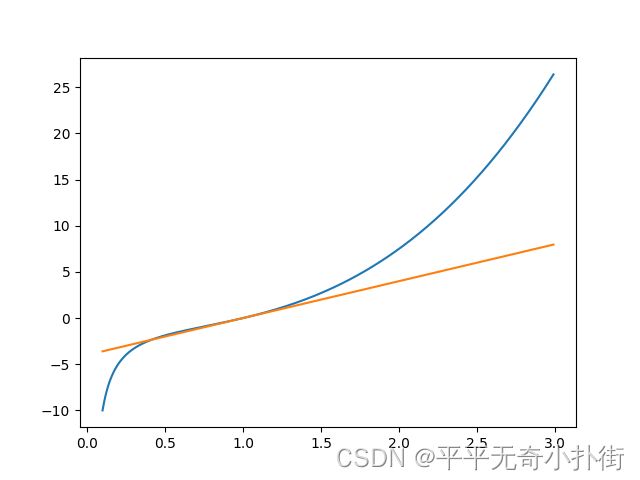
1.绘制函数 y=f(x)=x3−1/x 和其在 x=1 处切线的图像。

import numpy as np
from matplotlib import pyplot as plt

def get_function(x):
    return x**3 - 1/x

def get_tangent(function, x, point):
    h = 1e-4
    grad = (function(point+h) - function(point)) / h
    return grad*(x-point) + function(point)

x = np.arange(0.1,3.0,0.01)
y = get_function(x)
y_tangent = get_tangent(get_function, x=x, point=1)
plt.plot(x,y)
plt.plot(x,y_tangent)
plt.show()

2.求函数 f(x)=3x1^2+5ex2 的梯度。
$$\frac{\delta f}{\delta x_1}=6x_1$$

$$\frac{\delta f}{\delta x_2}=5e^{x_2}$$

$$则\frac{\delta f}{\delta x}=(6x_1,5e^{x_2})$$

3.函数 f(x)=||x||2 的梯度是什么？
$$设x=(x_1,x_2,...,x_n)$$

$$则f(x)=||x|{|}_2=\sqrt{x_1^2+x_2^2+...+x_n^2}$$

$$则\frac{\delta f}{\delta x}=(\frac{\sqrt{{\sum }_{i=1}^n{x}_i^2}}{\delta x_1},\frac{\sqrt{{\sum }_{i=1}^n{x}_i^2}}{\delta x_2},...,\frac{\sqrt{{\sum }_{i=1}^n{x}_i^2}}{\delta x_n})$$

$$则\frac{\delta f}{\delta x}=(\frac{1}{2}\ast 2x_1\ast (\sum _{i=1}^n{x}_i^2{)}^{-\frac{1}{2}},\frac{1}{2}\ast 2x_2\ast (\sum _{i=1}^n{x}_i^2{)}^{-\frac{1}{2}},...,\frac{1}{2}\ast 2x_n\ast (\sum _{i=1}^n{x}_i^2{)}^{-\frac{1}{2}})$$

$$则\frac{\delta f}{\delta x}=(\frac{x_1}{\sqrt{{\sum }_{i=1}^n{x}_i^2}},\frac{x_2}{\sqrt{{\sum }_{i=1}^n{x}_i^2}},...,\frac{x_n}{\sqrt{{\sum }_{i=1}^n{x}_i^2}})$$

$$则\frac{\delta f}{\delta x}=(\frac{x_1}{||x|{|}_2},\frac{x_2}{||x|{|}_2},...,\frac{x_n}{||x|{|}_2})=\frac{x}{||x|{|}_2}$$

4.你可以写出函数 u=f(x,y,z) ，其中 x=x(a,b) ， y=y(a,b) ， z=z(a,b) 的链式法则吗?
$$\frac{\delta u}{\delta a}=\frac{\delta u}{\delta x}\frac{\delta x}{\delta a}+\frac{\delta u}{\delta y}\frac{\delta y}{\delta a}+\frac{\delta u}{\delta z}\frac{\delta z}{\delta a}$$

$$\frac{\delta u}{\delta b}=\frac{\delta u}{\delta x}\frac{\delta x}{\delta b}+\frac{\delta u}{\delta y}\frac{\delta y}{\delta b}+\frac{\delta u}{\delta z}\frac{\delta z}{\delta b}$$

2.5 自动微分

1.为什么计算二阶导数比一阶导数的开销要更大？

二阶导数是一阶导数的导数，计算二阶导数需要用到一阶导数，所以开销会比一阶导数更大

2.在运行反向传播函数之后，立即再次运行它，看看会发生什么。

会报错，因为进行一次backward之后，计算图中的中间变量在计算完后就会被释放，之后无法进行二次backward了，如果想进行第二次backward，可以将retain_graph置为True，实验如下

①retain_graph默认为False

import torch
x = torch.randn((2, 3), requires_grad=True)
y = torch.square(x) - 1
loss = y.mean()
loss.backward()
loss.backward()

报错：

RuntimeError: Trying to backward through the graph a second time, but the saved intermediate results have already been freed. Specify retain_graph=True when calling .backward() or autograd.grad() the first time.

②retain_graph置为True

我们把两次backward的grad给分别打印出来，可以看到第二次的backward其实把梯度再次回传一遍叠加在了第一次backward上面

import torch
x = torch.randn((2, 3), requires_grad=True)
y = torch.square(x) - 1
loss = y.mean()
print(x)
loss.backward(retain_graph=True)
print(x.grad)
loss.backward()
print(x.grad)

tensor([[ 0.0294,  1.5586, -0.7047],
        [ 1.6767,  1.2802, -0.3465]], requires_grad=True)
tensor([[ 0.0098,  0.5195, -0.2349],
        [ 0.5589,  0.4267, -0.1155]])
tensor([[ 0.0196,  1.0391, -0.4698],
        [ 1.1178,  0.8535, -0.2310]])

3.在控制流的例子中，我们计算d关于a的导数，如果我们将变量a更改为随机向量或矩阵，会发生什么？

将变量a更改为随机向量或矩阵，会报错，实验如下

import torch
def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
a = torch.randn((3), requires_grad=True)
d = f(a)
d.backward()

RuntimeError: grad can be implicitly created only for scalar outputs

原因可能是在执行 loss.backward() 时没带参数，即可能默认是与 loss.backward(torch.Tensor(1.0)) 相同的，可以尝试如下的实验

import torch
a = torch.randn((3), requires_grad=True)
d = a**2
print(a)
d.backward(torch.ones_like(d))
print(a.grad)

tensor([ 1.1194, -0.2641,  0.2242], requires_grad=True)
tensor([ 2.2388, -0.5282,  0.4484])

那么代回上面的实验也是可行的

向量：

a = torch.randn((3), requires_grad=True)
d = f(a)
print(a)
d.backward(torch.ones_like(d))
print(a.grad)

tensor([ 0.7534, -1.3026, -1.2577], requires_grad=True)
tensor([51200., 51200., 51200.])

矩阵：

a = torch.randn((2, 3), requires_grad=True)
d = f(a)
print(a)
d.backward(torch.ones_like(d))
print(a.grad)

tensor([[-2.0677, -1.0871,  0.1289],
        [ 0.4897, -0.4152,  0.2643]], requires_grad=True)
tensor([[51200., 51200., 51200.],
        [51200., 51200., 51200.]])

4.重新设计一个求控制流梯度的例子，运行并分析结果。

设计的思路为，当参数order为1的时候求开二次方，当order为2的时候求平方。(简单应用if控制)

import torch
def f(x, order):
    if order == 1:
        y = torch.sqrt(x)
    elif order == 2:
        y = torch.square(x)
    else:
        return x
    return y

x = torch.randn(size=(), requires_grad=True)
print(x)
y = f(x, order=1)
y.backward()
print(x.grad)
x.grad.zero_() # 清除梯度
y = f(x, order=2)
y.backward()
print(x.grad)

tensor(-1.2684, requires_grad=True)
tensor(nan)
tensor(-2.5369)

5.使 f(x)=sin(x) ，绘制 f(x) 和 df(x)/dx 的图像，其中后者不使用 f′(x)=cos(x) 。

import numpy as np
from matplotlib import pyplot as plt

def get_function(x):
    return np.sin(x)

def get_derivative(function, x):
    h = 1e-4
    return (function(x+h) - function(x)) / h

x = np.arange(0.01,10.0,0.01)
y = get_function(x)
y_derivative = get_derivative(get_function, x)
plt.plot(x,y)
plt.plot(x,y_derivative)
plt.show()

2.6 概率

1.进行 m=500 组实验，每组抽取 n=10 个样本。改变 m 和 n ，观察和分析实验结果。

略

2.给定两个概率为 P(A) 和 P(B) 的事件，计算 P(A∪B) 和 P(A∩B) 的上限和下限。（提示：使用友元图来展示这些情况。)
$$max(P(A),P(B))⩽P(A\cup B)⩽P(A)+P(B)$$

$$0⩽P(A\cap B)⩽min(P(A),P(B))$$

3.给定两个概率为 P(A) 和 P(B) 的事件，计算 P(A∪B) 和 P(A∩B) 的上限和下限。（提示：使用友元图来展示这些情况。)
$$P(A,B,C)=P(C|A,B)P(A,B)=P(C|A,B)P(B|A)P(A)$$

$$由于C只依赖于B，则P(C|A,B)=P(C|B)$$

$$则P(A,B,C)=P(C|B)P(B|A)P(A)$$

4.在 2.6.2.6节中，第一个测试更准确。为什么不运行第一个测试两次，而是同时运行第一个和第二个测试?

因为在测试艾滋病病毒时候，第一个测试和第二个测试可以看作具有不同的特性(可以认为是不同测试针对的靶点有异)，再次使用第一个测试，如果没有随机因素的干扰或者测试流程的问题，结果应该是不会变的(因为针对的靶点是一样的)，这么看来同时使用第一个和第二个测试(针对的靶点有异)更具有说服力一点，这样假设条件独立更有可能，而重复第一个测试这两次会有较强的相关关系