一. data/newBGIseq500_1.fq和data/newBGIseq500_2.fq中是基于BGIseq500测序平台的一种真核生物基因组DNA的PE101测序数据,插入片段长度为450 bp;已知该基因组大小约在6M左右。
1) 请统计本次测序的PE reads数是多少对reads?
2) 理论上能否使基因组99%以上的区域达到至少40X覆盖?请简要写出推理和计算的过程与结果,数值计算使用R等工具时请写出所用代码。
wc -l data/newBGIseq500_1.fq|awk '{print $1/4}'
#结果为1599999
# 根据上一步结果计算全部的数据量 base<-1599999*200
#计算测序深度 dep<-base/6000000 #由于基因组dna长度长,某片段被检测到的概率p<<1,并且测序过程中会产生趋向无穷的reads,因此碱基被测到的深度符合泊松分布
#r语言的ppois()函数表示累积泊松分布函数,因此,要计算基因组碱基至少40X覆盖的概率,应先求出0-39X被覆盖的累积分布概率ppois(39,dep),再用1-此概率就是大于等于40X的概率,
即: 1-ppois(39, dep) [1] 0.975145
#因此,理论上认为,该数据量不能使基因组99%以上区域达到至少40X覆盖度
二.
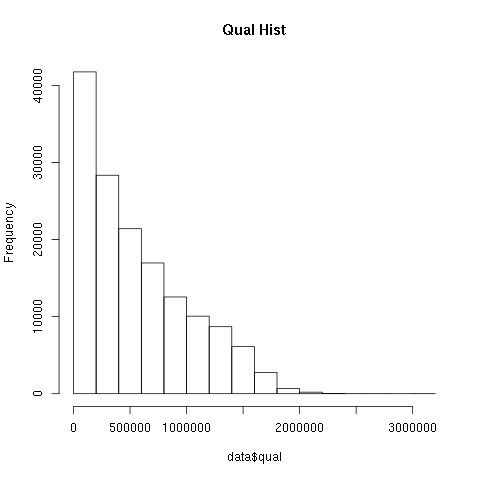
1)编写脚本或选择适当工具,统计 vcf 中变异位点的 Qual 值分布情况,并画图展示
zcat chr17.vcf.gz |grep -v '^#' | awk -F "\t" '{if (FNR == 1) print "POS\tqualq" ;else print $2,$6}' > chr17.qual
#! /usr/bin/env Rscript ## Qual.R png("qualstatistic-1.png") qualddata <- read.table(file ="chr17.qual",sep = '',header = T) #注意时空格分隔 head(qualddata);dim(qualddata);class(qualddata) colnames(qualddata) <- c('POS','QUAL') p <- hist(qualddata$QUAL,main = "Qual Hist") dev.off()
#方法二 ggplot
library(ggplot2)
ggplot(qualddata,aes(x=QUAL))+
# 直方图函数:binwidth设置组距
geom_histogram(binwidth = 200000,fill='lightblue',color='black')+
xlab("QUAL")+ylab("Frequency")
2)提取TP53基因的变异,说明变异位点是的数目(纯和和杂合)。
cat tp53_stat.sh #! usr/bin/bash for i in {10..12};do #echo $i cat tp54.vcf | grep '#CHROM' |awk -F "\t" '{print $'$i'}' echo -e "hom\t `cat tp54.vcf | grep '^chr17' |awk -F "\t" '{print $'$i'}' | grep -v '0/0' | awk -F ":" '{print $1}' | awk -F "/" '{if($1==$2){print $0}}' | wc -l`" echo -e "het\t `cat tp54.vcf | grep '^chr17' |awk -F "\t" '{print $'$i'}' | grep -v '0/0' | awk -F ":" '{print $1}' | awk -F "/" '{if($1!=$2){print $0}}' | wc -l`" done
bash tp53_stat.sh
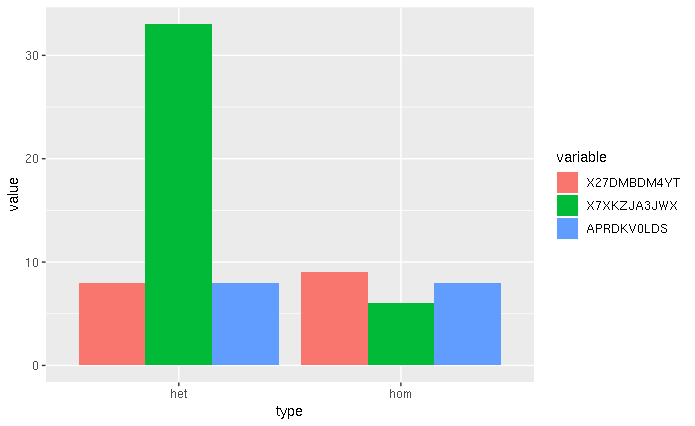
结果如下 27DMBDM4YT hom 9 het 8 7XKZJA3JWX hom 6 het 33 APRDKV0LDS hom 8 het 8
cat tp53_select_out.txt type 27DMBDM4YT 7XKZJA3JWX APRDKV0LDS hom 9 6 8 het 8 33 8
R画图
library(reshape) library(ggplot2) d1 <- read.table(file ="tp53_select_out.txt",sep = '\t',header = T) head(d1) #宽表格 整理成长表格 d1_m <-melt(d1,id.vars=c("type")) head(d1_m) ggplot(d1_m, aes(x=type, y=value)) + geom_bar(stat="identity", position="dodge", aes(fill=variable))#position: dodge: 柱子并排放置
题三:
#下载并安装 SOAPdenovo 软件 ,设置 -K参数为35对该数据 进行de novo组装 , #并画出组装结果序列从长到短的度累积曲线图。 #计算组装结果的 N50 #统计组装结果GC 含量分布,并画图展示
SOAPdenovo下载地址: https://sourceforge.net/projects/soapdenovo2/files/latest/download 安装: make 软件配置文件 #参考简书https://www.jianshu.com/p/30c74297513a SOAPdenovo 下载安装 与使用 ,config 配置说明 config 配置说明: 除了输入文件路径外,还包含以下几个参数的设置 1. avg_ins 文库插入片段的平均长度,在实际设置时,可以参考文库size分布图,取峰值即可 2. reverse_seq 是否需要将序列反向互补,对于pair-end数据,不需要反向互补,设置为0;对于mate-pair数据,需要反向互补,设置为1 3. asm_flags 1表示只组装contig. 2表示只组装scaffold,3表示同时组装contig和scaffold,4表示只补gap 4. rd_len_cutof 序列长度阈值,作用和max_rd_len相同,大于该长度的序列会被切除到该长度 5. rank 设置不同文库数据的优先级顺序,取值范围为整数,rank值相同的多个文库,在组装scaffold时,会同时使用。 6. pair_num_cutoff contig或者scaffold之前的最小overlap个数,对于pair-end数据,默认值为3;对于mate-paird数据,默认值为5 7. map_len 比对长度的最小阈值,对于pair-end数据,默认值为32;对于mate-pair数据,默认值为35
配置示例如下:cat config_file
#cat config_file max_rd_len=100 [LIB] avg_ins=450 asm_flag=3 map_len=32 ##### rd_len_cutoff=100 序列长度阈值,作用和max_rd_len相同,大于该长度的序列会被切除到该长度 pair_num_cufoff=3 reverse_seq=0 rank=1 q1=/home_extend/u****/R/exam/newBGIseq500_1.fq #注意使用上一步过滤后的 clean.fq q2=/home_extend/u****/R/exam/newBGIseq500_2.fq
运行 ./SOAPdenovo-63mer all -s config_file -K 35 -R -o /home_extend/u1010/R/exam/abc
结果
Version 2.04: released on July 13th, 2012 Compile Jul 9 2013 11:57:16 ******************** Pregraph ******************** Parameters: pregraph -s config_file -K 35 -R -o /home_extend/u****/R/exam/abc In config_file, 1 lib(s), maximum read length 100, maximum name length 256. 8 thread(s) initialized.
.......
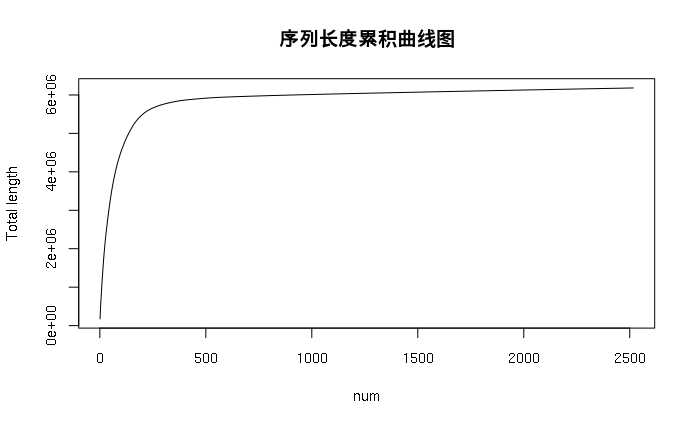
累计曲线与N50 计算:
#!/usr/bin/env/python #encoding=utf8 import sys #args = sys.argv #fasta_file = args[1] fasta_file = r'E:\pylab\testfq_data\abc.scafSeq' def read_fasta(): with open(fasta_file) as F_in: seq_name= '' seq = {} for line in F_in: if line.startswith(">"): seq_name=line.strip('\n').split(' ')[0][1:] seq[seq_name]='' else: seq[seq_name]+=line.strip('\n') return seq def get_seqname_len(): seq = read_fasta() seqname_length = {} seqname_length_sort ={} for k, v in seq.items(): seqname_length[k] = len(v) seqname_length_sort = sorted(seqname_length.items(), key=lambda x: x[1])#排序 seqname_length_sort = dict(seqname_length_sort) return seqname_length_sort def write_seqname_length(): seqname_length_sort = get_seqname_len() f = open('t5.txt', 'w') f.write('seq_name' + '\t' + 'length' + '\n') for k, v in seqname_length_sort.items(): f.write(k + '\t' + str(v) + '\n') f.close()
def calculate_n50(): sum_len = 0 n50 = 0 seqname_length_sort = get_seqname_len() for seqname,length in seqname_length_sort.items(): sum_len +=length L.append(length) for seqname, length in seqname_length_sort.items(): n50 += length count +=1 if n50 >= sum_len/2: print("n50序列名 : %s" % seqname + "\n" + "n50序列长度 : %s" % (seqname_length_sort[seqname])) break
calculate_n50()
结果:
n50序列名 : scaffold204
n50序列长度 : 40176
根据t5.txt 文件内容可知
# seq_name length
# min = C156737 100
# max = scaffold82 176232
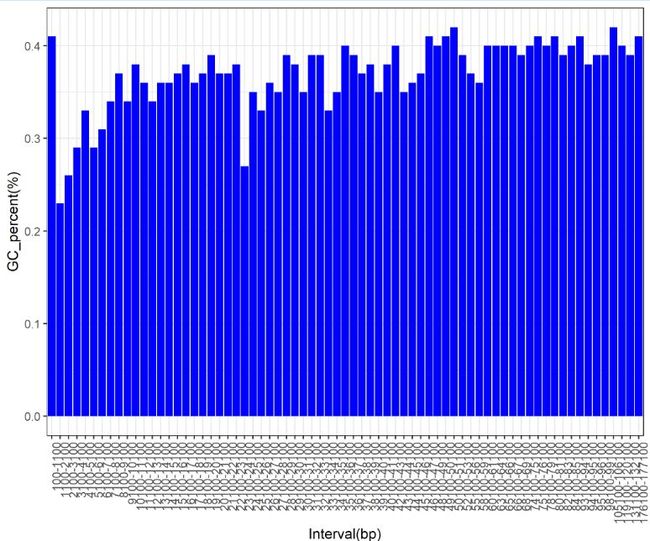
统计该区间的GC percent,存到文件 Interval_GC_percent.txt 中R作图
seq = read_fasta() def Interval_GC_count(): min = 100 max = 176232 extend = 1000 location = {}
while min < max :
count = 0 SUM_GC = 0 SUM_LEN = 0 regin = range(min, min + 1000) for name ,sequence in seq.items(): length = len(sequence) GC = sequence.count('G') + sequence.count('C') if length in regin: #count +=1 SUM_GC += GC SUM_LEN += length if SUM_LEN >0: OUT ="%.2f"%(SUM_GC/SUM_LEN) location[str(min) + '-' + str(min + 1000)] = OUT min +=1000 if min > max: break return location location= Interval_GC_count() def WRITE(): f = open('Interval_GC_percent.txt', 'w') f.write('Interval' + '\t' + 'GC_percent' + '\n') for k, v in location.items(): f.write(k + '\t' + str(v) + '\n') print('over') f.close()
R画图展示
setwd("D:/pycharm_ngs_programs/hg19_stat") d2 <- read.table(file = 'seqname_length_da2xiao.txt',sep = '\t',header = F) head(d2) cumsum_data <- cumsum(d2[,2]) #cumsum累加数据 cumsumframe <- as.data.frame(cumsum_data) #转换成数据框 head(cumsumframe);dim(cumsumframe);class(cumsumframe) df <- cbind.data.frame(cumsumframe,d2)#合并数据框 head(df);dim(df);class(df) plot(df$cumsum_data,type="l",ylab='Total length',xlab = 'Seq num',main="序列长度累积曲线图") #或者 l<-seq(1,nrow(df),by=1 ) plot(x=l,y=df$cumsum_data,type="l",ylab='Total length',xlab = 'num',main="序列长度累积曲线图")
readslength 区间 与GC_percent
d1 <- read.table(file = 'Interval_GC_percent.txt',sep = '\t',header = T) head(d1) order_level<- d1$Interval d1$Interval<- factor(d1$Interval,levels = order_level,ordered = T) str(d1) library(ggplot2) ggplot(d1,aes(x=d1$Interval,y=GC_percent))+ geom_bar(stat="identity",fill = "blue")+ theme(axis.text.x=element_text(angle=90,hjust = 1,vjust = 1))+ xlab("Interval(bp)")+ylab("GC_percent(%)") ggsave('Interval_gc_percent.png')
结果:
或者:
d1 <- read.table(file = 'Interval_GC_percent.txt',sep = '\t',header = T) head(d1);dim(d1) inter <- d1$Interval GC_percent <- d1$GC_percent plot(GC_percent,type="b",ylim=c(0.2,0.6),xaxt="n",yaxt="n",bty ='o', main="bty默认取\"o\"",xlab="长度",ylab="GC_percent") axis(side = 1,at=1:71,labels=inter,tick=TRUE,las = 2)