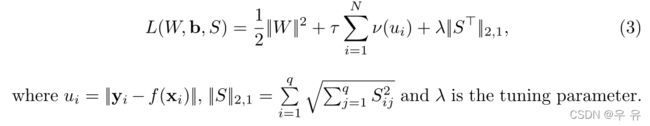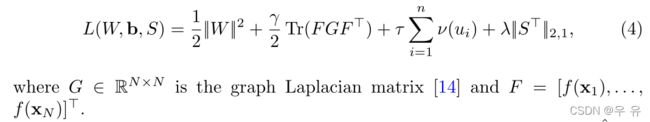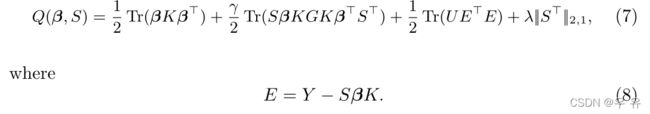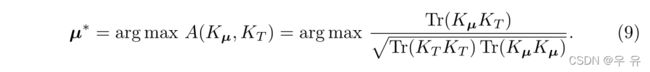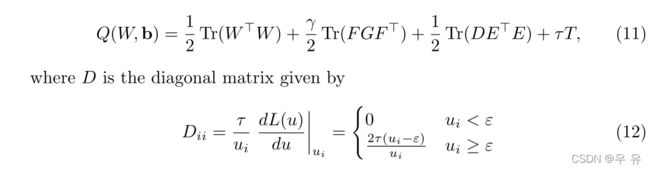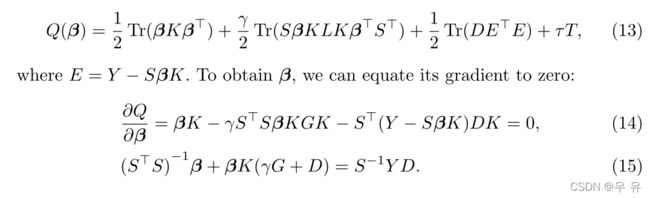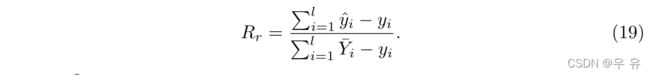【翻译】Direct Estimation of Spinal Cobb Angles by Structured Multi-output Regression
Direct Estimation of Spinal Cobb Angles by Structured Multi-output Regression
基于结构化多输出回归的脊柱Cobb角直接估计
文章链接、IPMI、Conference paper First Online: 23 May 2017
作者:
单词积累
vertebrae椎骨、scoliosis脊柱侧弯、quantitative定量qualitative定性、
derive from 从..获得、
摘要
Cobb角定量评估脊柱弯曲度,在脊柱侧凸的诊断和治疗中起着重要作用。传统的角度测量方法由于人工干预过多而存在较大的变动性和低可靠性。然而,由于椎体边界存在高度的模糊性(ambiguity)和变动性(variablity),自动获取Cobb角具有一定的挑战性。|| 在这篇文章中,我们阐述了从脊柱x射线估计Cobb角作为一个多输出回归任务。我们提出结构化支持向量回归(S2VR)来联合估计Cobb角和脊柱的x线标志在一个单一的框架。所提出的S2VR可以真实地处理输入图像与定量输出之间的非线性关系,同时显式地捕获输出图像的内在相关性。我们引入流形正则化(manifold regulization、论文、ppt、流形及流行正则化)来挖掘输出空间的几何特性。我们提出通过核对齐来学习S2VR中的核以提高其识别能力。|| 在439名脊柱侧凸患者的脊柱x线数据集上对该方法进行了验证,结果表明,该方法与专家人工获得的地面真实值的激励相关系数(coefficient)为92.76%,优于两种基线方法。我们的方法实现了Cobb角的直接估计,精度高,表明其在临床应用的巨大潜力。
1. 介绍
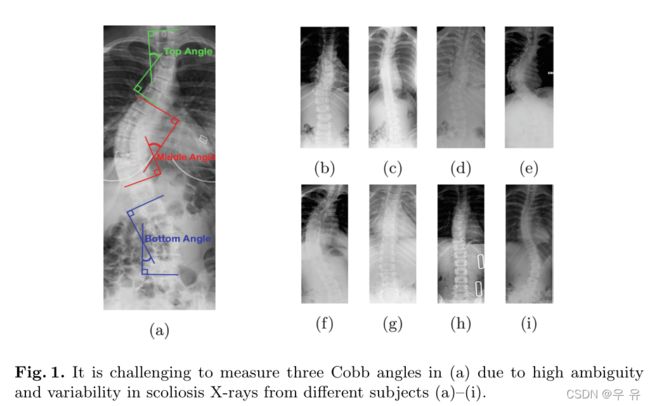
Cobb角被广泛用于脊柱侧凸的诊断和临床常规治疗决策。脊柱侧弯是一种结构性的、横向的、旋转的脊柱弯曲,尤其发生在青春期或青春期前后的儿童身上,并导致残疾。对于脊柱侧弯的临床检查,x线摄影(x线)是最常用的影像学检查技术,其获取成本低,时间成本[2]。我们忠实地使用Cobb角(图1(a))来量化脊柱畸形的大小[3],Cobb角来源于后前(后前)x光片,手动测量时选择脊柱顶部和底部相对水平线最倾斜的椎体来量化脊柱畸形的程度。
然而,传统的人工测量涉及到脊椎识别和测量角度的繁重干预,存在很大的变异性劳动密集型的高不可靠性。人工测量的准确性受到许多因素的影响,如椎骨的选择、不同观察者的偏差和不准确的量角器。
由于x射线具有高度的模糊性和变异性,自动估计科布角是一个挑战。如图1所示,大的解剖(anatomical)变异性和低的组织对比度会导致感兴趣椎骨区域的识别和进一步测量的复杂性。椎骨定位采用活动轮廓模型[4]、自定义滤波模型[5]和带电粒子模型[6]。角度是根据椎骨的坡度计算出来的。虽然这些方法可以自动获得Cobb角,但它们存在多个处理阶段的复杂性,计算成本较高。此外,对所有椎骨的多个目标进行分割是非常具有挑战性的,特别是在脊柱x光片结构不同和边界模糊的情况下。
在不进行滤波和分割的情况下,基于统计学习的直接估计方法[7-11]在最近的大规模图像数据中取得了巨大的成功,具有进行Cobb角估计的潜力。与传统的分割方法(如变分模型[12])相比,直接估计方法通过监督学习刻画了图像的出现与高级语义概念之间的关系,实现了高效的计算和压缩结构建模。通过对数据统计的研究,直接方法具有鲁棒性,能够处理模糊边界和区域异质性(region heterogeneity、异质性)。
cobb角的估计可以从地标坐标的预测中获益。由于脊柱图像的模 糊性和可变性,分别获取角度是一个挑战。从直观上看,cobb角度几乎与脊柱形状相对应,基本上可以用landmarks来描述。在本文中,我们通过同时最小化Cobb角和路标坐标的损耗来训练模型,这证明了我们的方法的鲁棒性。与现有的直接方法[7-10]相比,本文提出的方法联合估计路标角和Cobb角,不仅提高了预测精度,而且为放射科医生提供了角度估计的直观验证。
虽然现有的直接方法取得了很大的成功,但将它们直接应用于我们的任务有三个主要的限制。首先,这些方法不能明确地描述输出之间的相关性,而这正是判别学习所必需的。其次,它们忽略了输出值分布的内在几何性质,这将导致解的非光滑化,进而对角度估计产生负面影响。第三,内核参数,例如带宽,通常是手动设置的,这不能保证对不同的应用程序是最佳的。
在本文中,我们提出了结构化支持向量回归(S2VR)来直接预测脊柱的Cobb角和里程碑x线。与传统的支持向量回归(SVR)相比,S2VR在一个框架内实现了非线性映射和显式相关建模。特别是,非线性映射处理输入图像和高级输出(角度和地标)之间的关系,而显式相关建模捕获输出之间的相关性。总之,我们的工作在以下几个方面做出了贡献:
-我们通过多输出回归实现了联合自动估计Cobb角和脊柱标志物,这对直接从x线摄影评估脊柱曲率至关重要。
-我们提出了一种新的多输出回归模型S2VR,它可以同时处理非线性的输入输出关系和内在的输出间相关。该框架具有很强的通用性,可广泛应用于其它测量估计。
-通过探索输出空间的几何结构,我们将流形正则化引入到框架中,从而实现平滑的解决方案。
-为了提高性能,我们提出采用核目标对齐的方法来学习核,提高了核的鉴别能力。
2. 方法
本文提出的结构化支持向量回归(S2VR)方法,通过将预测构建为一个多输出回归任务,直接估计地标的Cobb角和坐标。S2VR包括非线性映射过程和显式相关学习阶段。引入流形正则化来探讨输出空间的内禀几何。由于我们的方法是建立在支持向量回归的基础上,我们基于核目标对齐来学习核。
2.1 结构化支持向量回归
在提出的S2VR中,我们提取了表示asxi∈Rd的x射线的图像特征。坐标和角度由yi∈Rqandyi= [h1,…,hc,v1,…]表示。Vc,a1,a2,a3],顺地标数,hiandviare第5个地标点的横轴和纵轴。另外,Cobb角个数为3,则q = 2c+ 3。回归的任务是从输入特征预测坐标和Cobb角。S2VR的框架如图2所示。
非线性输入输出关系学习的SVR
支持向量回归(SVR)被广泛应用于处理复杂的非线性关系。解决方案的稀疏性保证了它的有效性。SVR模型采用以下优化公式:
φ:Rd→RHis是到更高h维空间的非线性变换,W∈Rq×H,b∈Rq, φ(xi)∈RH,yi∈Rq,τ和n分别表示调优参数的正常数和训练样本个数。
显式交互输出相关学习的S2VR
我们引入一个结构矩阵xs, S∈Rq×qto,捕捉输出的内在相关性(角度和地标)。预测模型为esf(xi) =S(Wφ(xi)+b), S2VR模型可定义为:
λ是调谐参数。
优势
结构矩阵svia ?2,1-norm正则化是鼓励多个输出共享相似的参数稀疏模式。因此,结构,如空间相关性共享相似的特定模式,可以捕捉到稳健预测的角度和坐标。
S2VR的流形正则化
为了进一步提高算法的性能,我们考虑引入基于图拉普拉斯的流形正则化[13]项来建模输出空间的局部几何结构。研究表明,利用几何结构并考虑局部不变性可以显著提高学习性能。我们采用附加正则化的损失函数为:
其中g∈RN×Nis图拉普拉斯矩阵[14]an dF= [f(x1),…f (xN)] ?
在这里,我们选择由g =ˆD−E给出的非归一化图拉普拉斯矩阵,以相似图的形式表示labelsyi|i=1:Nof数据。我们简单地将所有具有正相似性的点连接起来,并通过yeij对所有边进行加权。相似函数是高斯函数eij = e xp(−| |yi−yj||2/(2ρ2)),其中参数ρ是函数的宽度。ˆDis由ˆDii=?N j = 1 eij。
优势
流形正则化利用了输出数据分布的几何形状。特别是,由于图像外观的高模糊性和可变性,输入特征和输出角度(地标)的分布可能在估计时不一致。因此,我们利用流形正则化的优势,保证了解相对于输出空间的平滑性。
2.2 内核化
由于图像特征输入与角度(地标)输出之间的关系复杂且高度非线性,我们对(4)进行核化以进行非线性回归。
内核S2VR
在内核化之前,我们根据跟踪重写(4):
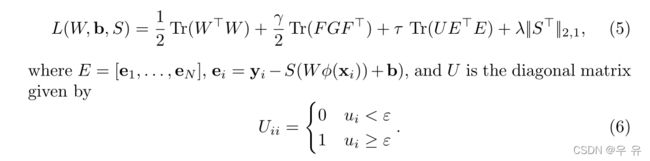 假设映射函数φ(xi)在某个无限维的RKHS中。根据代表定理[15],W=βΦ?(X),其中β∈Rq×NandX= [x1,…,xN]。定义核矩阵asK=Φ?(X)Φ(X)。我们用内核版本重写(5):
假设映射函数φ(xi)在某个无限维的RKHS中。根据代表定理[15],W=βΦ?(X),其中β∈Rq×NandX= [x1,…,xN]。定义核矩阵asK=Φ?(X)Φ(X)。我们用内核版本重写(5):
判别内核学习
我们重点学习给定基核的锥组合skz |z=1:Zto得到一个有效的核。因此,对于k =?Z Z =1μzKz,我们提出通过核对齐来学习与基本核相关的权系数μ,该方法在学习多个核的最优组合方面显示出了极大的有效性[16,17]。
提出了一种核对齐方法,通过最大限度的相似性将输入核对齐到目标核对齐,从而提供了一种最合适的获取μ权系数的方法。现在我们引入核对准公式来学习S2VR中的核。我们希望最大化目标核矩阵KT与核矩阵Kμ之间的对齐a (Kμ,KT)。优化问题可以表示为 :
定义目标kernelKT= Y?Y, whereY = (y1,…,yN)。
(9)中的目标函数可以等价地改写为:
其中||μ||= 1是正则项,μ≥0保证正确定性,对于i, j∈{1,···,Z},α由αi= T r?KiKT ?矩阵xv由vij = T r?KiKj ?。通过遵循[18],我们求助于一个更有效的二次规划问题来求解(10)。
优点
在S2VR中,通过核对齐对核进行监督学习,提高了核的识别能力。此外,自动学习内核函数中的参数比通过交叉验证进行调优更有效。
2.3 交替优化
采用一种新的交替优化方法对S2VR进行了有效的优化。该方法速度快,并对其收敛性进行了理论分析。最小化(7)可分解为核系数β和结构矩阵xs的两个子问题。
通过迭代重加权最小二乘(IR WLS)[19]优化求解β相关的最小化问题。我们构造了(5)a b u tui的二次逼近:
(D对角矩阵)
(这是一个常数项的和,它不依赖于任何一个工作。在内核版本中修改(11):)
它是标准的Sylvester方程(a β+βB=C,其中a = (S?S)−1,B=K(γG+D) an dC=S−1Y D)。
我们利用(15)的最优解构造一个降序方向来最小化(13),下一步的解由行搜索算法[18]计算。受到红外小波法的启发,我们提出了算法1中总结的改进的红外小波法。
其中是pjj =1 2||Sj||2的对角矩阵,P∈Rq×qandSjis s的列向量。
我们计算s(17)的导数。基于onS的计算。因此,newSis通过使用currentS来计算。程序总结在Algorithm2中。因此,最小化(7)可以通过交替优化βand来求解。
收敛性的证明
算法的快速收敛保证了算法的有效性。通过理论分析,证明了优化算法的收敛性。由于优化是用交替迭代的方法进行的,我们首先证明了改进的IRWLS方法在优化β方面的收敛性。
定理1.(13)中的q (β)将所有输出集合在一起,并且在算法1的每次迭代中单调递减。证明可以参考[19]中附录的证明。既然在定理1中保证了适应型IR WLS过程的收敛性,下面的定理说明了交替迭代法的收敛性。
定理2.(7)中的q (β,S)自下有界,且随着βand的每次交替迭代优化步骤单调减小。证明。由于Q(β,S)和n(13)的形成,我们得到了Q(β,S)≥0的界。设β(t)and (t)分别表示β和sin。然后,β(t)and (t)由β(t)←arg minβQ(β,S(t−1))and计算S (t)←arg minSQ(β(t−1),S)。由于在[20]中证明了eq (β,S(t−1))≥Q(β,S(t)),得到如下不等式:
Q(β(t),S(t))是单调递减的ast→+∞。因此,证明了q (β,S)优化的收敛性。
2.4 预测
在测试阶段,给定一个新的输入x(t),预测的角度和路标为ˆy(t)=SβK(t),其中ek (t)=?Z Z Z = 1μzK (t)、K (t) Z =Φ?(ˆX)φ(X (t))和ˆX为支持向量组成的矩阵。
3. 实验
S2VR在大量受试者的脊柱x光数据集上进行了验证。大量实验表明,该方法的有效性持续优于基线方法,可用于临床脊柱侧凸的分析。
3.1 数据集和实现细节
脊柱后前位x线数据集由来自不同个体的439个样本组成。由于颈椎(颈椎骨)很少发生脊柱畸形[21],我们选择了17个由胸椎和腰椎组成的椎骨进行脊柱形态表征。每个脊椎骨由四个角上的标志来定位。脊柱界标由c= 68个点手工标注,Cobb角由人类专家测量,从上到下分别为TA、MA、BA。由于面向梯度直方图(histogram of oriented gradient, HOG)描述符具有很强的局部表示能力,我们选择它作为模型的输入。选择高斯核作为基本核,σ参数在[0.1,1]范围内。我们的模型已经用留一交叉验证方案进行了验证。
3.2 实验结果
S2VR在脊柱x线数据集上取得了良好的性能,并在Cobb角估计和地标检测方面表现出了良好的效果。地标检测的定性结果如图3所示。我们还与两种基线方法进行了比较,表明了我们的方法在脊柱曲率分析上的优势。
比较/对照
如表1所示,我们比较了两种baseline方法,即支持向量回归(SVR)[19]、形状回归机(SRM)相对均方根误差(RRMSE)和相关系数[23],表明了该方法的有效性。对于长度为l的向量,设ˆy,y,¯y分别表示ground truth,估计向量,目标变量leyover train data的均值,RRMSE定义为:
S2VR的平均RRMSE最低为21.63,相关系数最高为92.76。由于输出之间存在很强的相关性,S2VR中显式相关学习可以忠实地利用结构信息,获得更好的结果。此外,经过学习的、更健壮的内核足够强大,可以处理图像外观和高级语义概念之间的对应关系。我们还对分离预测和联合预测进行了比较。从两个表中可以看出,联合预测始终优于分离预测。
有效性
该方法在脊柱x线数据集上的优异性能验证了该方法的有效性。将该方法估计的Cobb角与人工测量的Cobb角进行了比较。估计角与地面真值的相关性分别如图4所示。该方法获得了中间角的相关系数为0.923,其余两个角的相关系数分别为0.884和0.902。
4. 结论
在本文中,我们提出结构化支持向量回归(S2VR),直接预测Cobb角和里程碑的脊柱x射线图像特征。提出的S2VR包括非线性映射和显式结构建模,能够处理特征与定量评价参数之间的高度非线性关系,并显式学习输出间的校正。此外,引入流形正则化来实现平滑解。为了获得判别核,我们提出在S2VR中通过核目标对齐来学习核,这可以利用监督核学习的优势。在脊柱x线数据集上的大量实验表明,与两种基线方法相比,我们的方法具有显著的有效性。