小波分析在电力系统暂态信号处理中的应用

前面我们主要讲了小波分析在机械振动信号或者其他时间序列中的应用

基于小波包特征提取和随机森林的CWRU轴承数据集故障识别 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/556172942

基于小波区间相关（Interval-Dependent）的信号降噪方法 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/558132966

多元小波降噪方法 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/558075972

基于小波分析和深度学习的时间序列分类并可视化相关特征 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/557922791

小波相干分析在时间序列分析中的应用 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/557902264

小波降噪基础-python版本 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/552373046

使用最大离散重叠小波变换MODWT和支持向量回归 SVR的金融时间序列预测 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/552759437

基于小波变换的稳健的单导联心电图 (ECG) 描绘 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/553061958

基于小波变换和机器学习的地震信号处理和识别 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/553158878

基于小波分析和机器学习的时间序列分析与识别 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/554097033

本文我们主要谈下小波在电力系统暂态信号处理中的应用，先不涉及任何数学公式，避免劝退。

20 世纪 90 年代以来，小波分析理论及其工程应用逐渐受到各国数学家和工程技术人员的高度重视。 小波分析被认为是对傅里叶分析的重大突破，与短时傅里叶变换相比，小波变换提供了一个可调的时间频率窗。 当观察高频信号时，时窗自动变窄；当研究低频信号时，时窗自动变宽，即具有变焦距的特点。 小波变换的另一特征是能表征信号的奇异性，即信号在不同尺度上小波变换的模极大值或Lipschitz指数可以表示信号的突变特征。 小波变换应用于电力系统的研究最近几年得到了很好的发展，更在分析和处理暂态信号领域显示了优越性和广阔的应用前景，主要应用领域包括电力信号去噪、数据压缩、电力设备故障诊断、电能质量扰动信号分析、继电保护、故障定位等。

信号去噪

电力信号的理想状态只包含工频 50Hz信号，但在实际情况中，一般是包含工频基波分量、 各次谐波分量、 故障暂态分量（系统故障时包含）和噪声的混合信号。 去噪的目的是在噪声背景下提取有用的工频基波、 各次谐波或是高频暂态分量，使提取的信息内尽可能的不含噪声。 Wintkin最早提出了利用小波分析中不同尺度信号的空间相关性去噪的思想，随后Mallat提出了小波模极大值去噪法。 其依据是小波变换的模极大值集中体现了信号的奇异性，白噪声的性态与信号的奇异性态在小波变换下具有截然不同的性质，即噪声信号所产生的小波变换模极大值随尺度的增大而减小，而其他信号引起的小波变换模极大值随尺度的增大而增大（对于阶跃信号保持不变）。

电能质量信号分析

在电能质量评估方面，Santoso首先提出小波变换是评估电能质量的有效方法，并将双正交小波用于检测、 定位和识别不同原因造成的电能质量问题； 2000 年，他利用Fourier变换和小波变换对电能质量扰动进行特征提取后，提出了完整的基于小波变换的神经网络分类器实现方法。引起电能质量下降的各种扰动本质上是一种包含奇异点的暂态扰动信号。当小波函数取作平滑函数的一阶导数时，小波变换系数的模极大值点对应的就是信号的奇异点，也就是信号的突变点。

目前由于分布式发电的兴起，电力电子器件与非线性负载的大量使用，电力系统中的谐波污染也日益严重。 谐波对电力系统的安全、经济运行造成了很大的影响，已成为电能质量的公害。 而在电力系统中谐波检测方法大多通过快速Fourier变换及其改进算法实现，它对于谐波出现的时刻和时变谐波估计问题的解决无法满足应用的要求。 1994年，Ribeiro P. F. 首次指出小波变换是分析电力系统非平稳谐波畸变的新工具。之后，小波变换在谐波检测方面得到了深入的研究。 由于小波变换是以频带的方式处理频域信息且不需要整周期采样，故与Fourier变换相比，在一定的条件下，小波变换可获得较为稳定的谐波检测结果。

继电保护

传统的继电保护原理是基于对工频信号及稳态分最的分析计算，将故障产生的高频分量当作干扰滤掉。 常用方法有Fourier变换、 Kalman滤波、 最小二乘滤波和有限脉冲响应滤波等，这些都是处理平稳信号的实用方法。 对面向提取和识别电力系统复杂非平稳暂态信息的新一代继电保护而言，仅满足于利用工频或稳态分量来实现保护，就会在实现诸如行波和超高速保护时，为解决快速动作与可靠性的矛盾方面碰到困难，也难以实现变压器差动保护中励磁涌流的准确判别。 而小波变换为近年发展起来的暂态保护实现和发展提供了有力的手段。

故障行波信号到达检测点时将呈现突变的情况，如果对该信号进行小波分析并求模极大值，则行波信号的突变处将会出现模极大值的特点。 这样，小波变换模极大值与故障行波信号的主要特征 “突变点” 产生了 联系，对行波的分析就转换为对小波变换模极大值的分析。 于是，依据小波变换模极大值在不同尺度下的大小，可确定行波保护起动条件，根据模极大值点的极性，构成电流行波比较式行波保护，准确判别故障区域。

小波变换应用到变压器励磁涌流的判别中，能够充分利用小波对奇异信号检测的优点，使保护在励磁涌流期间可靠闭锁。 由于变压器空载合闸差动电流具有间断特征，内部故障时电流波形是连续变化的，因而励磁涌流和内部故障时差动电流的小波系数表现出不同特征。

故障定位

（1）故障选线。 目前在电网故障信息分析及管理系统中，故障选线主要采用负序比相算法来实现。 其依据是只有在故障线路的正方向上才满足故障后第一周期的负序电压相量滞后负序电流相量 90°~120°的条件。故障选线也可通过比较各回线路行波信号小波变换模极大值来实现。 从幅值上看，非故障线路的电流行波信号仅为故障线路行波的透射分量，因此相应的小波变换模极大值也较小，而故障线路的电流行波信号小波变换模极大值较大。

（2）故障选相。

（3）故障测距。 电力系统要求及时、 准确地得知线路故障位置以便用最短的时间清除故障，尽快恢复供电， 现已有可用于解决实际问题的各种故障测距方法。小波变换模极大值大小与模极大值的极性可以很好地表示输电线路故障行波信号的主要特征突变点， 因此可以利用小波变换来进行行波故障测距 。 主要思路是运用小波变换对此类具有奇异性、 瞬时性的故障信号加以分解， 得到在不同尺度上用小波变换模极大值表示的故障信息， 利用小波奇异点检测确定线路故障发生的时刻及其两次行波波头到达检测点的时间间隔，从而推算出故障位置，达到故障定位的目的。

数据压缩

电力系统中为了记录完整的扰动信息， 通常需要1~4MHz的采样率， 这就使得到的数据量很大， 如此庞大的数据向调度中心上传时， 不但占用数据通道时间长， 且容易造成通道阻塞， 这就对数据压缩的效率提出了严峻挑战。 电力系统中现有扰动监测仪的数据约简技术多采用重叠方法， 即对现有数据不断覆盖， 或采用量化技术， 即把一系列相同的波形看成个整体。 这两种方法的确节省了存储空间，但却不是一般意义上的数据压缩。 对于平稳变化的工频正弦信号， Fourier 变换是一个有效的数据压缩工具。 但当系统故障后， 用 Fourier 变换压缩数据将造成数据丢失。利用小波变换实现数据压缩的方法一般是将信号进行小波分解后绝对值小于阙值的变换系数置零，仅将非零系数的位置及其数值记录下来， 然后对信号进行重构。对实际电力系统信号， 其压缩后的数据长度只有原信号的1/6~1/3, 相应的压缩率达到3~6倍， 经重构得到的恢复信号与原始信号的归一化均方误差小于10^(-6)。

电力设备故障诊断

电力设备（如电机）故障诊断就是分解和处理电力系统基本设备在运行中产生的各种电磁、 机械、 声音等信号， 实时地判别其状态。 电力设备正常运行时发出的信号（如振动）较平稳， 且设备异常， 必将产生故障暂态信号。 对故障暂态信号作多分辨分析， 可以显示故障信号的突变幅度和时间，从而达到设备故障诊断的目的。 小波分析在电力设备故障诊断方面，目前主要集中在对发电机、电动机、 变压器和电流互感器的诊断上。此外，还被应用于断路器故障诊断和各种局部放电检测中。

待解决的问题

小波变换巳在电力暂态分析中得到成功的应用，展示了小波变换在该领域的广阔应用前景。暂态信号的小波分析是一个很有应用价值的研究方向，但仍存在一些问题：

（1）小波变换的数学基础理论及信号处理机理。小波并非尽善尽美，小波基础理论尤其是复小波基础理论还有待于完善。

（2）小波基选择原则。小波基是小波变换的核心。电力系统暂态信号分析一方面需要对小波基（包括复小波基）的时频特性、相位特征进行研究；另一方面，需要结合电力系统种类繁多的暂态信号的特点，寻找或构造与信号相似的小波基，使小波变换域能量尽量集中，改善暂态信号特征提取精度。

（3）特征提取算法。 利用连续小波变换、 离散小波变换、 多分辨分析、 小波包变换、 奇异检测等方法，研究有效、 可靠的特征提取算法，提取电力系统故障暂态、 谐波及扰动的特征信息，为故障诊断、 继电保护、 谐波分析等提供有效的预处理算法。

（4）系统运行方式和故障类型的自动识别和诊断。 随着电力系统的高速发展，系统运行方式及故障类型变得愈加复杂。 结合神经网络、 模糊判别、 模式识别等智能技术及非线性理论，研究利用小波变换信息的智能暂态信号分类识别系统，进行系统运行方式和故障类型的自动识别和诊断，以实现复杂的自适应继电保护。 这是小波变换在电力系统暂态信号分析中应用的潜力所在。

（5）实时性研究。 小波变换应用于继电保护，具有采样率要求高、 计算蜇大、 对不同保护启动判据建立比较困难的特点，因而对工程应用中小波变换快速算法的研究提出了要求。另外，结合DSP的发展，开发专门的处理芯片，也是小波变换在电力系统继电保护中应用的一个研究方向。

（6）电力系统其他应用。 基于小波变换的信号分析在电力系统其他诸多领域同样具有巨大的应用潜力。 如小波变换的多尺度概念非常适合于电力系统暂态稳定预测、 动态安全性分析、 负荷预测等方面，其变焦距特性能辨别和追踪系统变扯的微弱变化，提高电力系统动态安全分析、 暂态稳定与负荷预测的实时性和准确性。

此外，本文给出一些信号降噪方法，代码面包多下载，链接见评论区

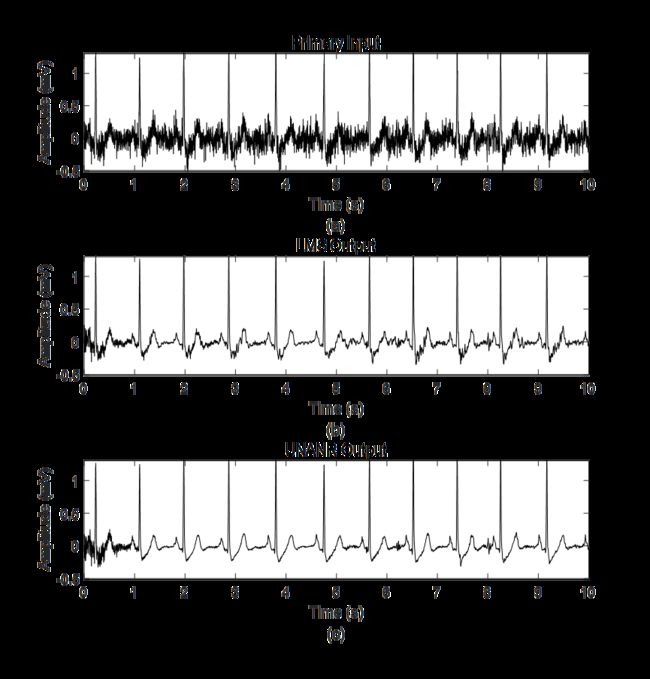
基于一种无偏归一化方法的自适应ECG信号降噪

程序运行环境为MATLAB R2018a，执行一种无偏归一化方法的自适应ECG信号降噪，附带参考文献。

基于离散小波变换的ECG信号处理（删除伪影，检测ECG信号的PQRST波并确定患者的心跳）

程序运行环境为MATLAB R2018a，采用离散小波变换（最大重叠离散小波变换）对ECG信号进行处理，包括删除伪影，滤波降噪，检测ECG信号的PQRST波并确定患者的心跳等。

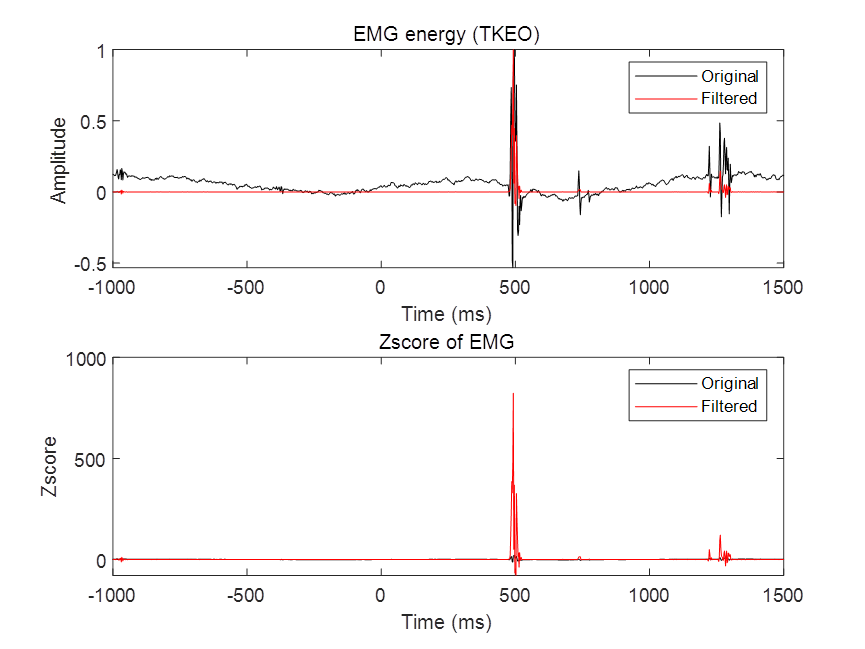
基于Teager-Kaiser能量算子 (TKEO)的肌电信号EMG降噪方法

程序运行环境为MATLAB R2018a，执行基于Teager-Kaiser能量算子 (TKEO)的肌电信号EMG降噪

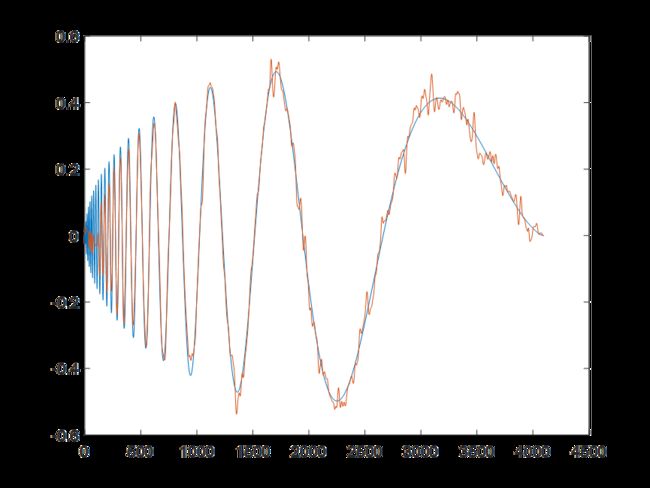
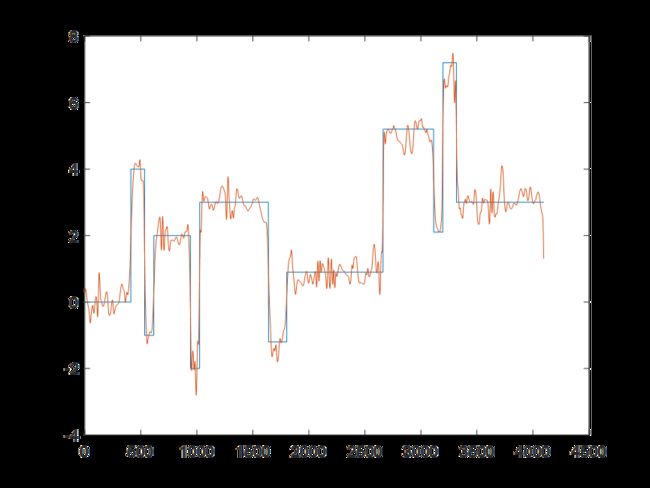
基于变分模态分解和Cramer von Mises检验的一维信号降噪方法

程序运行环境为MATLAB R2018a，采用变分模态分解和Cramer von Mises检验对一维信号进行降噪处理，附带参考文献