自博弈学习初步

如有错误，欢迎指正
本文学习过程中的归纳总结
如有侵权，请私信本人
参考链接：https://blog.csdn.net/weixin_37837522/article/details/91907661
https://www.jianshu.com/p/bcbc41125c54
https://zhuanlan.zhihu.com/p/30282616
对于alphazero的准备知识重点看这一篇
https://blog.csdn.net/windowsyun/article/details/88701321
简单的alphazero实现
https://zhuanlan.zhihu.com/p/32089487
理解框架
https://blog.csdn.net/ikerpeng/article/details/81387170

虚拟博弈（Fictitious play， FP）是在规范式博弈（单步博弈）中学习纳什均衡的常用方法。虚拟玩家们选择最优反应（都以最大化自身利益为原则而做出的动作）。FSP将单步博弈拓展到多步博弈（extensive-form game，扩展式博弈）。

NFSP agent由两个网络组成。第一个网络（Q网络，这里有点像critic网络）是采用强化学习的方式、用过往与其他玩家博弈的经历来训练，这个网络用来学习一个近似最优反应（best response strategy）；第二个网络采用监督学习的方式、用自己过往的博弈经历训练，这个网络（policy网络，有点像Actor，输出动作的概率分布）用来学习一个自己过往策略的平均策略（average strategy）。NFSP agent结合自己的平均策略和最佳反应策略综合来做出行动。

NFSP 就是引入神经网络近似函数的 FSP，是一种利用强化学习技术来从自我博弈中学习近似纳什均衡的方法。解决了三个问题：

• 无先验知识 NFSP agent 学习
• 运行时不依赖局部搜索
• 收敛到自我对局的近似纳什均衡

虚拟自我对局 Fictitious Self Play, FSP

虚拟对局是从自我对局中学习的博弈论模型。自我对局的参与人选择针对其对手的平均行为的最佳反应。自我对局参与人的平均策略在某些类型的博弈（如二人零和博弈和多人势力场博弈）中都会收敛到纳什均衡。Leslie 和 Collins 在 2006 年给出了推广的弱化自我对局。这种模型和通常的自我博弈有着类似的收敛保证，但是允许有近似最优反应和扰动的平均策略更新，也让这个扩展模型对机器学习尤其合适。

自我对局通常使用规范式博弈定义，这与扩展式博弈在有效性上存在指数级差距。Heinrich 等人在 2005 年引入了 Full-Width Extensive Form FSP（XSP），可以让自我对局参与人使用行为式，扩展式进行策略更新，得到了线性的时间和空间复杂性。这里一个关键的洞察是对规范式策略的凸组合，σ-nf= λ1 π-nf1 + λ2 π-nf2，我们可以达到一个实现等价的行为策略 σ，通过设置该值为成比例于对应的实现概率的凸组合，

其中 λ1xπ1(s) + λ2xπ2(s) 是在信息状态 s 的策略的规范化常量。除了在行为策略下定义自我对局的 full-width 平均策略更新外，公式(1) 给出了从这样的策略的凸组合中采样数据集的一种方法。Heinrich 等人在 2015 提出了 Fictitious Self Play （FSP）的基于采样和机器学习的算法来近似 XFP。FSP 分别用强化学习和监督学习来替换最优反应计算和平均策略更新。特别地，FSP agent 产生他们在自我对局中的经验转换的数据集。每个 agent 存放了自身的转移元组 (st,at,rt+1,st+1) 在记忆 MRL 中 ，这个为强化学习设计。而 agent 自身的行为 (st,at) 被存放在另一个分开的记忆 MSL 中，这为监督学习设计。自我对局的采样通过 agent 的强化学习的记忆来近似用其他参与人的平均策略组合定义的 MDP 的数据。因此，通过强化学习的 MDP 的近似解会产生一个近似的最优反应。类似地，agent 的监督学习记忆近似了 agent 本身的平均策略，这可以通过监督式的分类方法学习。

NFSP将FSP与神经网络近似相结合。在算法1中，游戏的每个玩家都由单独的NFSP agent控制，这些agent从与其他玩家博弈中学习，即self-play。每个NFSP agent与其他agents交互，将经历（st,at,rt+1,st+1）存在MRL中，再将自己的最优反应（st,at)存在MSL中。NFSP将这两个记忆MRL和MSL视为两个不同的数据集，分别用于深层强化学习和监督分类。（两者存放方式不一样，MRL是buffer的形式，先进先出；MSL用蓄水池reservoir的形式，每个样本重要性一致）

NFSP用MRL去训练一个DQN，从而可以得到近似最优反应 β=ε-greedy(Q), 也就是ε的概率随机选动作，（1-ε）的概率选择Q值最大的动作。（Q网络输入为s，输出Q值，loss为|Q(s)-(rt+Q(st+1))|2）

NFSP再用MSL通过监督分类的方式去训练另一个网络 Π(s,a|θΠ)去模拟自己过往最优反应。该网络将状态映射到动作概率并定义agent的平均策略 π=Π。（ Π网络的输入为s，输出在各动作上的概率分布P，loss为-logP, 这里不是-R*logP，因为MSL中都是由Q网络估计而得到的近似最优反应经历，他们重要性相同，可以理解为每一个的R都等于1）

神经网络虚拟自我对局

进行了多种扩展：神经网络函数近似，reservoir 采样，anticipatory 动态性和完全基于 agent 方法。NFSP agent 和博弈中的其他参与人进行交互，并记住自身关于博弈状态转移的经验和自身的行为。NFSP 将这些记忆分成两个数据集——一个给深度强化学习，一个给监督学习使用。特别地，这个 agent 从 MRL 的数据中使用 off-policy 强化学习训练一个神经网络 FQ 来预测行为值，Q(s,a)。得到的网络定义了 agent 的近似最优策略 β = ε-greedy(FQ)，这里根据概率 ε 选择随机行动，根据概率 1 - ε 选最大化预测行为值的行动。NFSP agent 训练了另外一个神经网络，FS 在 MSL 的数据中使用监督学习来模拟自己过去的行为。这个网络将状态映射到了行动概率上，定义了 agent 的平均策略，π = FS。在博弈进行过程中，agent 从两个策略 β 和 π 的混合中选择策略。

尽管虚拟参与人通常是针对对手的平均策略进行最优反应，但在连续时间的动态虚拟对局参与人是对对手平均规范式策略 π-nft-i + η d/dt π-nft-i短期预测的最优反应。研究表明，选择合适的，博弈相关的 η 可以提高在均衡处的自我对局的稳定性。NFSP 使用 β-nft+1i- π-nfti ≈ d/dt π-nfti 作为用在 anticipatory 动态中的离散时间导数近似值。注意 Δ π-nfti ∝ β-nft+1i - π-nfti 是常见的离散时间自我对局的规范化更新方向。为了让一个 NFSP agent 计算近似对对手预测平均策略组合 σ-i ≡ π-nf-i + η(β-i - π-nf-i)的最优反应， βi，agent 需要迭代求值并最大化其行动值，Q(s,a) ≈ Eβi,σ-i[Gti|St=s, At=a]。这个可以使用 off-policy 强化学习，如 Q-learning 或者 DQN 在和对手的预测策略，σ-i 对局的经验上获得。为了确保 agent 的强化学习记忆，MRL，包含这种类型的经验，NFSP 需要所有的 agent 从 σ≡ (1 - η)π-nf + η (β-nf)选择他们的行动，其中 η ∈ R 被称为预测参数（anticipatory parameter）。

虚拟自我对局通常要保留平均规范式博弈的最优反应策略，π-nfTi = 1/T Σt=1T βti。Heinrich 等人在 2015 年给出了使用采样和机器学习技术来产生数据并学习用展开式博弈形式表示的规范式博弈策略凸组合。例如，我们可以通过使用 βti, t = 1,…,T 按照 1/T 的比例来采样整个博弈的过程来产生展开式数据。NFSP 使用 revervoir 采样来记忆其平均最优反应的经验。agent 的监督式学习记忆，MSL 是一个 reservoir 仅仅会在采用其近似最优策略 β 时增加经验。NFSP agent 通常会训练自己的平均策略网络 π=FS 来匹配其存储在自身监督学习记忆中的平均行为，例如通过优化过去行为的对数概率来进行训练。算法 1 给出了 NFSP，其中使用 DQN 作为强化学习的方法。

作者：朱小虎XiaohuZhu
链接：https://www.jianshu.com/p/bcbc41125c54
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

alphaGo Zero实现方式

主要的做法是:

• 利用蒙特卡洛树搜索建立一个模型提升器。
• 在自我对弈过程中，利用提升器指导模型提升，模型提升又进一步提高了提升器的能力。

简单博弈论概念：

• 信息对称（Perfect information / Fully information）是指游戏的所有信息和状态都是所有玩家都可以观察到的，因此双方的游戏策略只需要关注共同的状态即可，而信息不对称（Imperfect information / Partial information）就是玩家拥有只有自己可以观察到的状态，这样游戏决策时也需要考虑更多的因素。
• 零和（zero-sum），就是所有玩家的收益之和为零，如果我赢就是你输，没有双赢或者双输，因此游戏决策时不需要考虑合作等因素。
• 纳什平衡（Nash equilibrium）又称为非合作博弈均衡，是博弈论的一个重要术语，以约翰·纳什命名。在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略，那么这个组合就被定义为纳什平衡。

极大极小值算法：博弈过程中对方烜令我收益小的，我选收益大的
alpha-beta剪枝：在极大极小值算法中裁剪去不需要继续搜索的路径

蒙特卡罗方法

就是利用随机采样的样本值来估计真实值，理论基础是中心极限定理，样本数量越多，其平均就越趋近于真实值。

对于围棋，我们可以简单的用随机比赛的方式来评价某一步落子。从需要评价的那一步开始，双方随机落子，直到一局比赛结束。为了保证结果的准确性，这样的随机对局通常需要进行上万盘，记录下每一盘的结果（比如接下来的落子是黑子，那就根据中国规则记录黑子胜了或输了多少子），最后取这些结果的平均，就能得到某一步棋的评价。最后要做的就是取评价最高的一步落子作为接下来的落子。也就是说为了决定一步落子就需要程序自己进行上万局的随机对局，这对随机对局的速度也提出了一定的要求。和使用了大量围棋知识的传统方法相比，这种方法的好处显而易见，就是几乎不需要围棋的专业知识，只需通过大量的随机对局就能估计出一步棋的价值。再加上诸如All-Moves-As-First等优化方法，基于纯蒙特卡洛方法的围棋程序已经能够匹敌最强的传统围棋程序。

蒙特卡洛树探索（MCTS）也就是将以上想法融入到树搜索中，利用树结构来更加高效的进行节点值的更新和选择。

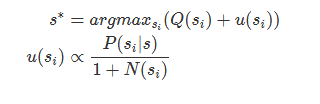
这里的s指的是一个state。从一个state做一个action，就会迁移到另一个state。Q是累积平均胜率，u则是对于Q的偏移，也就是选择让Q+u最大的一步棋。其中P(si|s)是策略网络的输出，探索刚开始时，策略网络的影响比较大，而随着探索的进行，策略网络的影响慢慢降低，偏移慢慢变小，而真正在模拟中取得更好胜率的落子会更容易被选中。N(si)是所有的模拟中(s,a)所指向节点的访问次数。

AlphaGo Zero 的网络结构

它的主体是MCTS，在训练过程中，将会重复这一过程上万次。
选择：
假设当前棋面状态为xt，以xt作为数据起点，得到距今最近的本方历史7步棋面状态和对方历史8步棋面状态，分别记作xt−1，xt−2，···，xt−7和yt，yt−1，···，yt−7。并记本方执棋颜色为c，拼接在一起，记输入元st为{xt，yt，xt−1，yt−1，···，c}。并以此开始进行评估。
扩展：
使用基于深度神经网络的蒙特卡罗树搜索展开策略评估过程，经过1600次蒙特卡罗树搜索，得到当前局面xt的策略πt和参数θ下深度神经网络fθ(st)输出的策略函数pt和估值vt。
模拟：
由蒙特卡罗树搜索得到的策略πt，结合模拟退火算法，在对弈前期，增加落子位置多样性，丰富围棋数据样本。一直持续这步操作，直至棋局终了，得到最终胜负结果z。
反向传播：
根据上一阶段所得的胜负结果z与价值vt使用均方和误差，策略函数pt和蒙特卡罗树搜索的策略πt使用交叉信息熵误差，两者一起构成损失函数。同时并行反向传播至神经网络的每步输出，使深度神经网络fθ的权值得到进一步优化。

AlphaGo Zero的应用

AGZ算法本质上是一个最优化搜索算法，对于所有开放信息的离散的最优化问题，只要我们可以写出完美的模拟器，就可以应用AGZ算法。所谓开放信息，就像围棋象棋，斗地主不是开放信息，德扑虽然不是开放信息，但本身主要是概率问题，也可以应用。所谓离散问题，下法是一步一步的，变量是一格一格，可以有限枚举的，比如围棋361个点是可以枚举的，而股票、无人驾驶、星际争霸，则不是这类问题。Deepmind要攻克的下一个目标是星际争霸，因为它是不完全信息，连续性操作，没有完美模拟器（随机性），目前在这方面AI还是被人类完虐