图像去噪——Neighbor2Neighbor: Self-Supervised Denoising from Single Noisy Images
一种用于图像降噪的自监督学习方法
Nb2Nb Neighbor2Neighbor
- Noise2Noise Revisit
- Proposed Method
-
- Generation of Training Image Pairs
- Self-Supervised Training with a Regularizer
Noise2Noise Revisit
Noise2Noise的核心思想是,对于一个未观察的干净场景 x \mathbf{x} x和观察到的两张独立含噪图像 y , z \mathbf{y,z} y,z,在噪声是服从零均值的情况下,用配对训练的降噪网络 ( y , z ) \mathbf{(y,z)} (y,z)和用配对训练的网络 ( y , x ) \mathbf{(y,x)} (y,x)是等价的。Noise2Noise的优化目标是: arg min θ E x , y , z ∥ f θ ( y ) − z ∥ 2 2 (1) \underset{\theta}{\arg \min } \mathbb{E}_{\mathbf{x}, \mathbf{y}, \mathbf{z}}\left\|f_{\theta}(\mathbf{y})-\mathbf{z}\right\|_{2}^{2} \tag{1} θargminEx,y,z∥fθ(y)−z∥22(1)由于Noise2Noise要求每一个场景 x \mathbf{x} x至少有2张独立的含噪图像 y , z \mathbf{y,z} y,z,这在真实场景中也难以满足。因此,为了增加Noise2Noise的实用价值,我们考虑对Noise2Noise的理论进行一定的扩展,主要考虑以下两个方面:
- 同一场景的两张独立含噪图像相似场景的两张独立含噪图像;
- 每个场景多张含噪图像每个场景单张含噪图像。
我们首先考虑第一点,即相似场景的两张独立含噪图像的情况。假设有一个干净图像 x x x,其对应的含噪图像是 y , z \mathbf{y,z} y,z,即 E y ∣ x ( y ) = x \mathbb{E}_{\mathbf{y} \mid \mathbf{x}}(\mathbf{y})=\mathbf{x} Ey∣x(y)=x,当引入一个非常小的图像差 ϵ ≠ 0 \epsilon\neq0 ϵ=0 时, x + ϵ \mathbf{x}+\epsilon x+ϵ是另一张含噪图像 z \mathbf{z} z对应的干净图像,即 E z ∣ x ( z ) = x + ε \mathbb{E}_{\mathbf{z} \mid \mathbf{x}}(\mathbf{z})=\mathbf{x}+\varepsilon Ez∣x(z)=x+ε,则有: E x , y ∥ f θ ( y ) − x ∥ 2 2 = E x , y , z ∥ f θ ( y ) − z ∥ 2 2 − σ z 2 + 2 ε E x , y ( f θ ( y ) − x ) (2) \begin{aligned} \mathbb{E}_{\mathbf{x}, \mathbf{y}}\left\|f_{\theta}(\mathbf{y})-\mathbf{x}\right\|_{2}^{2} &=\mathbb{E}_{\mathbf{x}, \mathbf{y}, \mathbf{z}}\left\|f_{\theta}(\mathbf{y})-\mathbf{z}\right\|_{2}^{2}-\boldsymbol{\sigma}_{\mathbf{z}}^{2} \\ &+2 \varepsilon \mathbb{E}_{\mathbf{x}, \mathbf{y}}\left(f_{\theta}(\mathbf{y})-\mathbf{x}\right) \end{aligned} \tag{2} Ex,y∥fθ(y)−x∥22=Ex,y,z∥fθ(y)−z∥22−σz2+2εEx,y(fθ(y)−x)(2)上式表明,在相似含噪图像 y , z \mathbf{y,z} y,z所对应的干净图像( x \mathbf{x} x和 x + ϵ ) \mathbf{x}+\epsilon) x+ϵ)并不相等的情况下,通过 ( y , z ) (\mathbf{y,z}) (y,z)直接构造训练对使用Noise2Noise训练降噪网络并不能得到与 ( y , x ) (\mathbf{y,x}) (y,x)配对相同的结果。进一步分析可以发现,当 ε → 0 \varepsilon \rightarrow 0 ε→0时, 2 ε E x , y ( f θ ( y ) − x ) → 0 2 \varepsilon \mathbb{E}_{\mathbf{x}, \mathbf{y}}\left(f_{\theta}(\mathbf{y})-\mathbf{x}\right) \rightarrow \mathbf{0} 2εEx,y(fθ(y)−x)→0,此时 ( y , z ) (\mathbf{y,z}) (y,z)配对可以作为Noise2Noise的一种近似。因此,一旦找到合适的满足"相似但不相同"条件的 y , z \mathbf{y,z} y,z, 就可以训练降噪网络。
对于单张含噪图像而言,构造两张"相似但不相同"的图像的一种可行方法是采样。在原图的相邻但不相同的位置采样出来的子图很显然满足了相互之间的差异很小,但是其对应的干净图像并不相同的条件(即 ε → 0 \varepsilon \rightarrow 0 ε→0 )。给定一张含噪图像 y \mathbf{y} y ,我们构造出一对近邻采样器 g 1 ( ∗ ) , g 2 ( ∗ ) g_1(*),g_2(*) g1(∗),g2(∗),采样出两张子图 g 1 ( y ) , g 2 ( y ) g_1(\mathbf{y}),g_2(\mathbf{y}) g1(y),g2(y),我们直接用这两张子图构造配对,以类似Noise2Noise的方式训练降噪网络,则有: arg min θ E x , y ∥ f θ ( g 1 ( y ) ) − g 2 ( y ) ∥ 2 (3) \underset{\theta}{\arg \min } \mathbb{E}_{\mathbf{x}, \mathbf{y}}\left\|f_{\theta}\left(g_{1}(\mathbf{y})\right)-g_{2}(\mathbf{y})\right\|^{2}\tag{3} θargminEx,y∥fθ(g1(y))−g2(y)∥2(3)这种方式成为Pseudo Noise2Noise。由于 g 1 ( y ) , g 2 ( y ) g_1(\mathbf{y}),g_2(\mathbf{y}) g1(y),g2(y)采样的位置不同,即
ϵ = E y ∣ x ( g 2 ( y ) ) − E y ∣ x ( g 1 ( y ) ) ≠ 0 \epsilon=\mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left(g_{2}(\mathbf{y})\right)-\mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left(g_{1}(\mathbf{y})\right) \neq \mathbf{0} ϵ=Ey∣x(g2(y))−Ey∣x(g1(y))=0直接应用Pseudo Noise2Noise的方式训练,得到的去噪模型不是最优的,会导致过度平滑。因此我们考虑在loss上增加正则项的方式对这种情况进行修正。假设有一个理想的降噪网络 f θ ∗ f^*_\theta fθ∗,它具有理想的降噪能力,即: f θ ∗ ( y ) = x and f θ ∗ ( g ℓ ( y ) ) = g ℓ ( x ) , l ∈ { 1 , 2 } f_{\theta}^{*}(\mathbf{y})=\mathbf{x} \text { and } f_{\theta}^{*}\left(g_{\ell}(\mathbf{y})\right)=g_{\ell}(\mathbf{x}),l\in\{1,2\} fθ∗(y)=x and fθ∗(gℓ(y))=gℓ(x),l∈{1,2},则这个理想的降噪网络 f θ ∗ f^*_{\theta} fθ∗满足: E y ∣ x { f θ ∗ ( g 1 ( y ) ) − g 2 ( y ) − ( g 1 ( f θ ∗ ( y ) ) − g 2 ( f θ ∗ ( y ) ) ) } = g 1 ( x ) − E y ∣ x { g 2 ( y ) } − ( g 1 ( x ) − g 2 ( x ) ) = g 2 ( x ) − E y ∣ x { g 2 ( y ) } = 0 (4) \begin{array}{l} \mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left\{f_{\theta}^{*}\left(g_{1}(\mathbf{y})\right)-g_{2}(\mathbf{y})-\left(g_{1}\left(f_{\theta}^{*}(\mathbf{y})\right)-g_{2}\left(f_{\theta}^{*}(\mathbf{y})\right)\right)\right\} \\ =g_{1}(\mathbf{x})-\mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left\{g_{2}(\mathbf{y})\right\}-\left(g_{1}(\mathbf{x})-g_{2}(\mathbf{x})\right) \\ =g_{2}(\mathbf{x})-\mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left\{g_{2}(\mathbf{y})\right\}=0 \end{array}\tag{4} Ey∣x{fθ∗(g1(y))−g2(y)−(g1(fθ∗(y))−g2(fθ∗(y)))}=g1(x)−Ey∣x{g2(y)}−(g1(x)−g2(x))=g2(x)−Ey∣x{g2(y)}=0(4)考虑在Pseudo Noise2Noise基础上增加一个约束,即: min θ E y ∣ x ∥ f θ ( g 1 ( y ) ) − g 2 ( y ) ∥ 2 2 , s.t. E y ∣ x { f θ ( g 1 ( y ) ) − g 2 ( y ) − g 1 ( f θ ( y ) ) + g 2 ( f θ ( y ) ) } = 0 (5) \begin{array}{l} \min _{\theta} \mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left\|f_{\theta}\left(g_{1}(\mathbf{y})\right)-g_{2}(\mathbf{y})\right\|_{2}^{2} \text {, s.t. } \\ \mathbb{E}_{\mathbf{y} \mid \mathbf{x}}\left\{f_{\theta}\left(g_{1}(\mathbf{y})\right)-g_{2}(\mathbf{y})-g_{1}\left(f_{\theta}(\mathbf{y})\right)+g_{2}\left(f_{\theta}(\mathbf{y})\right)\right\}=0 \end{array}\tag{5} minθEy∣x∥fθ(g1(y))−g2(y)∥22, s.t. Ey∣x{fθ(g1(y))−g2(y)−g1(fθ(y))+g2(fθ(y))}=0(5)此时,带约束的优化问题转化为带正则的优化问题:

Proposed Method
(a):训练流程的完整视图。一对子采样图像 g 1 ( y ) , g 2 ( y ) g_1(y),g_2(y) g1(y),g2(y)由噪声图像y生成,相邻子采样器 G = ( g 1 , g 2 ) G=(g_1,g_2) G=(g1,g2). 去噪网络分别以 g 1 ( y ) g_1(y) g1(y)和 g 2 ( y ) g_2(y) g2(y)作为输入和目标。正则化的损失L包括以下两项:在左侧,计算网络输出和有噪声目标之间的重构项 L r e c L_{rec} Lrec. 在右侧,进一步添加了正则化项 L r e g L_{reg} Lreg,考虑到次采样噪声图像对之间的真实像素值的本质差异。需要提到的是,出现两次的邻居子采样器G(绿色)代表相同的邻居子采样器。(b)推理使用训练好的去噪网络。最好的颜色。
训练策略上,从单张含噪图像 y y y通过采样器G构造出两张子图 g 1 ( y ) g_1(y) g1(y)和 g 2 ( y ) g_2(y) g2(y),通过这两个子图构造重建损失函数;之后,对原图[公式]进行推理降噪,得到的降噪图像再通过同样的采样过程G生成两张子图,最后计算正则项。训练好的网络可直接用于图像降噪,无需进行后处理。
Generation of Training Image Pairs
首先,我们引入一个邻居子采样器从单个噪声图像y中生成噪声图像对 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y))用于训练,满足假设:1)次采样配对噪声图像 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y))是有条件独立的; g 1 ( y ) g_1(y) g1(y)和 g 2 ( y ) g_2(y) g2(y)的底层真实图像之间的差距很小。使用相邻子采样器的图像对生成图如下图所示。表示图像为 y y y,宽度为W,高度为H. 相邻的子采样器 G = ( g 1 , g 2 ) G=(g_1,g_2) G=(g1,g2)的详细信息描述如下:
- 图像y被分成 W / k × H / k W/k×H/k W/k×H/k的小块,每个cell的大小为k×k. 根据经验,我们设置了k=2.
- 对于第i行和第j列单元格,随机选择两个相邻的位置。它们分别作为子采样器 G = ( g 1 , g 2 ) G=(g_1,g_2) G=(g1,g2)的 ( i , j ) (i,j) (i,j)个元素。
- 对于所有的 W / k × H / k W/k×H/k W/k×H/k单元格,重复步骤2。然后生成相邻的子采样器 G = ( g 1 , g 2 ) G=(g_1,g_2) G=(g1,g2). 给定图像 y \mathbf{y} y,推导出两个大小为 W / k × H / k W/k×H/k W/k×H/k的次采样图像 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y)).
这样,我们就可以使用不同的随机邻居子采样器从单个有噪声的图像中生成有噪声的训练图像对。成对图像 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y))的真值是相似的,因为 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y))的成对像素是原始噪声图像y中的邻居。此外,如果我们进一步假设噪声图像y是有条件的像素级独立的,则满足 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y))的独立要求。
对于采样器G,我们设计了近邻采样,即将图像划分成 2 × 2 2\times 2 2×2的单元,在每个单元的四个像素中随机选择两个近邻的像素分别划分到两个子图中,这样构造出来两张"相似但不相同"的子图,我们称他们为"Neighbor".

使用相邻的子采样器 G = ( g 1 , g 2 ) G=(g_1,g_2) G=(g1,g2)生成图像对的示例。这里,k=2和在每个2×2单元格中,随机选择两个相邻的像素,分别用红色和蓝色填充。将填充红色的像素作为子采样图像 g 1 ( y ) g_1(y) g1(y)的像素,将填充蓝色的其他像素作为另一个子采样图像 g 2 ( y ) g_2(y) g2(y)的像素。次采样的配对图像 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y))显示为右侧的红色补丁和蓝色补丁。
Self-Supervised Training with a Regularizer
由于我们已经在第4.1节中使用我们提出的邻居子采样器从单个噪声图像中生成训练图像对,在这里我们将引入带有噪声训练输入和目标的自监督训练策略。给定来自有噪声图像y的一对子采样图像 ( g 1 ( y ) , g 2 ( y ) ) (g_1(y),g_2(y)) (g1(y),g2(y)),我们使用以下正则化损失来训练去噪网络:
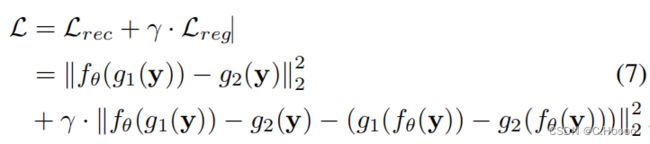
其中, f θ f_θ fθ是一个具有任意网络设计的去噪网络,而 γ γ γ是一个控制正则化项强度的超参数。为了稳定学习水平,我们停止了 g 1 ( f θ ( y ) ) g_1(f_θ(y)) g1(fθ(y))和 g 2 ( f θ ( y ) ) g_2(f_θ(y)) g2(fθ(y))的梯度,并在训练过程中逐渐将γ增加到指定的值。该训练框架如算法1所示。

