硬件损伤条件下的大规模信息超 表面辅助通信系统优化设计

---

$\text{硬件损伤条件下的大规模信息超表面辅助通信系统优化设计}$

---

---

:::

background

随着5G通信网络进入商业化阶段，为了获得更快和更可靠的数据传输，下一代（6G）通信技术已经处于研究状态。近年来，随着新型电磁材料技术的飞速发展，可重构智能超表面（Reconfigurable
Intelligent
Surface，RIS）以其准无源、可编程、低热噪声、低功耗、易部署的特征引起了学术界和工业界的广泛关注[@zongshu1][@zongshu2][@zongshu3]。2018年11月，日本移动运营商NTT
DoCoMo和智能雷达创业公司MetaWave演示了meta-structure（元结构）技术在28GHz带宽的通信系统的应用。

RIS应用场景

传统通信场景中,RIS可以[@zongshu4]：

1. 部署在基站与覆盖盲区之间，通过有效的反射/透射使传输信号到达覆盖空洞中的用户。

2. 部署在基站和边缘用户或弱覆盖区之间，既可以调整电磁单元的相位进行波束赋型来增强信号，又可以增加反射路径来提高信号质量。

3. 部署在建筑物的玻璃表面，它能有效接收基站传输的信号并透射到室内,实现室内覆盖增强。

4. 在业务密集的热点区域，可通过RIS增加额外的无线通信路径与信道子空间，从而提高信号传输的复用增益。尤其在视距传输场景中，引入基于RIS的可控信道，收发天线阵列间信道的空间相关特性将得到很大改善，可增加用于数据传输的子空间数目，极大提升系统及用户的传输性能。

5. 可与大规模MIMO天线技术相结合。通过超表面引入一定相移实现任意方向的聚焦波束发射,克服收发天线数量增加带来的成本和功耗增大问题，并提升MIMO的空间分集增益且聚焦波束的灵活性更强.

与此同时，RIS可以应用于高精度定位、车联网通信、无人机通信、安全通信、减少电磁污染、降低移动边缘网络时延等崭新的应用场景。

与众所周知的大规模多输入多输出（MIMO）技术[@MIMO1]、[@MIMO2]相比，RIS可以提供出色的系统性能，而不需要功率放大器等耗电部件。因此，RIS辅助系统的资源分配设计最近引起了极大的研究兴趣。例如，在许多最近的工作[@zhubeidong11]-[@anquan5]中已经研究了各种RIS辅助通信系统的传输优化。具体来说针对RIS辅助的单用户MISO系统，接收信噪比最大化[@zhubeidong11]、[@zhubeidong2]和服务质量(QoS)约束的功率最小化问题[@zhubeidong1]。关于由RIS辅助的多用户MISO系统，不同的设计目标，发射功率最小化[@zhubeidong1]、[@zhubeidong14]、可实现速率最大化[@rate]、[@WSR1]、[@rate2]和能量效率最大化[@efficiency1]、[@efficiency2]已经被采用来优化波束成形方案。除了单用户和多用户系统之外，在[@anquan1]-[@anquan5]中还研究了用于IRS辅助的多天线窃听信道的波束形成优化，其中设计目标是最大化系统可实现的安全速率。[@unifred]从宏观角度提出了一种MIMO系统中一般功率约束条件下的RIS辅助收发机设计的统一框架。关于RIS辅助的Multi-antenna
Simultaneous Wireless Information and Power
Transfer(SWIPT)系统，[@SWIPT]的作者执行波束成形优化以最大化由能量收集接收器接收的加权和功率，同时满足信息解码接收器的QoS约束。如上述工作所示，由于RIS的相移不仅与发射波束成形耦合，而且它们还应满足单位模量约束或属于离散集合[@zhubeidong2]、[@zhubeidong14]、[@WSR1]、[@efficiency2]，RIS的存在使最优波束成形设计复杂化。

然而，在实际通信系统中，收发信机硬件组件，例如放大器、振荡器、数模转换器和模数转换器等，不可避免地存在硬件损伤和非线性失真等问题[@sunshang25]、[@sunshang26]。与接收端传统噪声不同，硬件损伤会同时导致发送和接收信号的失真，通常，收发信机硬件损伤导致的信号失真程度与有效信号的发射/接收功率成比例。目前已经有诸多文献研究硬件损伤对MIMO系统的影响[@sunshang27]、[@sunshang28]、[@sunshang29]。在RIS辅助的大规模MIMO通信系统中，如果不谨慎处理收发信机中的硬件损伤，主动发射波束赋形设计和被动RIS波束赋形设计性能均会受到影响，进而导致通信系统性能的显著下降([@sunshang1]的仿真中损失超过2dB)。作为补救措施，[@sunshang30]-[@sunshang33]的作者对诸如多小区MIMO和MIMO中继系统进行收发机优化，以便减轻由硬件损伤引起的性能恶化。
通常而言，针对硬件损伤条件下的RIS辅助的大规模MIMO通信系统，由于RIS反射单元系数和收发波束赋形矢量需要联合优化，传统多天线系统收发信机设计方案无法直接应用。同时，考虑到硬件损伤引起的系统失真，现有完美硬件假设下的算法也无法直接解决硬件损伤下的收发信机和RIS优化。

文献[@sunshang1]首次正式提出硬件损伤下RIS辅助通信多天线系统波束形成优化问题，提出了硬件损伤下发射波束形成和IRS反射波束形成的非凸联合优化框架，对于源发射波束形成推导出了其闭式最优解，对于RIS反射波束形成的优化，通过求解单凸问题得到了最优目标值的上界。提出了一种低复杂度的minorization-maximization（MM）算法来逼近上界。

在这篇论文中，我们基于上述的观察，结合硬件损伤引起的信号失真，研究了RIS辅助的多天线通信系统的波束形成优化。源发射波束形成和RIS反射波束形成都被优化以最大化用户的接收SNR。与文献[@zhubeidong11]在硬件完善的假设下的工作相比，由于硬件损伤的存在，本文所考虑的问题更加复杂，并且不能直接用文献[@zhubeidong11]中提出的方法求解.另一方面，现有的稳健设计，[@sunshang30]-[@sunshang33]，因为传统的多天线系统不适用于RIS辅助系统，因为RIS相移也需要优化，这即使对于完美的硬件情况也是不可忽视的。

aim and content

aim

本毕业设计针对未来无线通信大容量、低成本、高能效、低功耗、灵活部署、高安全等各类需求，针对硬件损伤的特点，着重开展硬件损伤背景下智能反射面(RIS)辅助无线通信研究。灵活运用合适的凸优化方法在不损失解最优性的前提下减少复杂度。将非凸优化、凸优化理论与RIS辅助通信系统的仿真相结合。
深入挖掘硬件损伤条件下RIS辅助通信的信道资源关键特征，
完成不同通信场景的对抗硬件损伤的通信系统设计方案研究，一定程度上减轻由硬件损伤引起的性能恶化；并基于完美和非完美信道状态信息，提出高速率、高鲁棒硬件损伤下RIS辅助通信
系统优化设计方案；
通过上述研究，构建硬件损伤下智能反射面辅助通信系统的多维理论分析框架，
针对未来移动通信系统在不同应用场景下高速率、高可靠、低延时等信息
传输需求，在抵抗硬件损伤带来的性能恶化的方案设计方面取得一系列创新成果，
推动我国领跑后 5G 时代通信技术并促进无线通信产业的可持续发展。

content

本毕业设计课题将要求学生结合RIS与多天线收发信机硬件损伤的特点，针对单用户(Multiple-Input
Single-Output, MISO)系统收发信机均存在硬件损伤的情况，
提出低复杂度的联合收发信机波束赋形矢量和大规模RIS反射单元系数优化方案，利用计算机仿真验证所提方案的可行性，并比较所提方案与传统无RIS辅助的单用户MISO系统最优传输方案的性能差距，比较所提出的方案与不考虑硬件损伤的情况下的性能差距。

方案

拟通过合理的数学建模，以理论分析、算法设计和仿真验证相结合
的方式，深入研究硬件损伤条件下的 RIS
辅助通信系统的基础理论与关键技术，并通过搭建
系统级仿真平台，验证各种算法和方案的可行性、有效性，并分析算法的复杂
度和鲁棒性。为了详细地阐述拟采取的研究方案，本小节以多用户接入 RIS
辅助通信系统为例，具体系统模型与研究方案如下所述。

系统模型

多用户下的系统模型

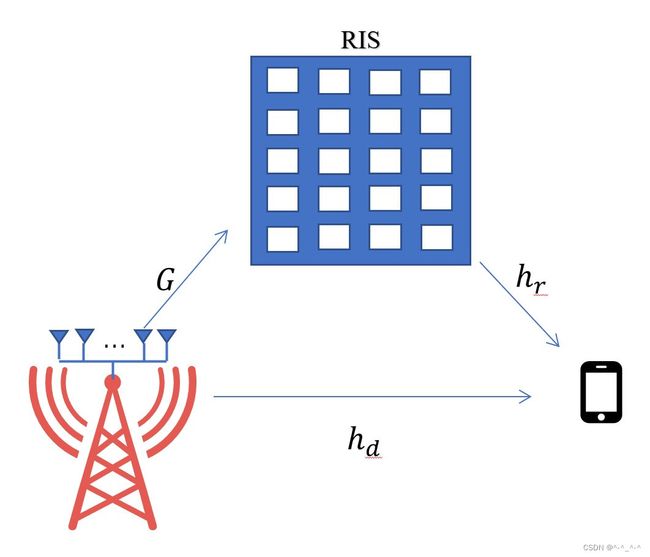
首先考虑RIS辅助的多用户MISO通信系统，建模方式同[@WSR1][@zhubeidong1],系统中有一个接入基站（Access
Point, AP）与 $K$ 个 合法单天线用户通信，并在合法用户附近布置 RIS
用于辅助基站通信。其中AP端有$M$个天线,RIS配备有$N$个反射单元。假设所有信道均服从准静态平坦衰落，从AP到用户$k$,从AP到RIS，从RIS到用户$k$的等效信道分别表示为${\mathbf{h}}_{\mathrm{d},k}\in {\mathbb{C}}^{M\times 1}$,$\mathbf{G}\in {\mathbb{C}}^{M\times 1}$,${\mathbf{h}}_{\mathrm{r},k}\in {\mathbb{C}}^{N\times 1}$。RIS的反射系数（相移）矩阵表示为对角阵$\mathbf{\theta }=\mathrm{diag}\left({\theta }_1,\cdots ,{\theta }_n,\cdots ,{\theta }_N\right)$，其中${\theta }_n=e^{ȷ{\phi }_n}$是RIS上第$n$个反射阵元的相位，在RIS第$n$个阵元的反射行为与用${\theta }_n$乘以瞬时信号，然后以RIS为源将合成信号继续传递。

发送到用户$k$的数据符号表示为$s_k$，是零均值单位方差（功率）的独立随机变量。
${\mathbf{w}}_k\in {\mathbb{C}}^{M\times 1}$是对应的发送波束形成向量。
与早先[@WSR1][@zhubeidong1]中RIS辅助通信的工作不同，本次毕业设计考虑了实际收发信机硬件损伤（Hardware
Impairments）的影响，信源AP处的发射信号表示为：
$$\mathbf{x}=\sum _{k=1}^K{\mathbf{w}}_k{s}_k+{\mathbf{z}}_s$$

其中${\mathbf{z}}_s$表示独立于$s_k,k=1,2,3,\cdots ,K$的干扰噪声,表征了功放噪声的共同作用效果，DAC和功放中的非线性，以及示波器的相位噪声，因此${\mathbf{z}}_s$中的元素都是独立零均值高斯随机变量，并且其中第$i$个元素的方差和AP端第$i$个天线处的预期发送信号功率成比例，例如：KaTeX parse error: Undefined control sequence: \overparen at position 63: …0}, \kappa_{S} \̲o̲v̲e̲r̲p̲a̲r̲e̲n̲{\operatorname{…
,其中${\kappa }_S\in \left(0,1\right)$表示发送干扰噪声的归一化方差。

在第k个用户处接收到的信号为

$$\begin{array}{rlr}{y}_k& =\underset{\text{Direct link }}{{\mathbf{h}}_{\mathrm{d},k}^{\mathrm{H}}\mathbf{x}}+\underset{\text{RIS-aided link }}{{\mathbf{h}}_{\mathrm{r},k}^{\mathrm{H}}\mathbf{\theta }\mathbf{G}\mathbf{x}}+u_k+z_{d,k}& \\ & =\left({\mathbf{h}}_{\mathrm{d},k}^{\mathrm{H}}+{\mathbf{h}}_{\mathrm{r},k}^{\mathrm{H}}\mathbf{\theta }\mathbf{G}\right)\left(\sum _{k=1}^K{\mathbf{w}}_k{s}_k+{\mathbf{z}}_s\right)+u_k+z_{d,k}& =\widetilde{y_k}+z_{d,k}\end{array}$$

$z_{d,k}$表示独立于
$\widetilde{y_k}$的第$k$个用户处的接收干扰噪声，它表征了AGC噪声、ADC和AGC中的非线性、示波器相位噪声的联合作用，$z_{d,k}$服从零均值高斯分布，$z_{d,k}$的方差和无干扰的接收信号成比例，例如：$z_{d,k}\sim \mathcal{C}\mathcal{N}\left(0,{\kappa }_D\mathbb{E}\left\{|\tilde{y}{|}^2\right\}\right)$,其中${\kappa }_D\in (0,1)$表示接收干扰噪声的归一化方差

其中，$u_k\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_0^2\right)$表示第$k$个用户接收机处的加性高斯白噪声(AWGN)，为了便于求解上述问题，本次毕设中定义$\mathbf{\theta }={\left[{\theta }_1,\cdots ,{\theta }_N\right]}^{\mathrm{H}}$,并且
${\mathbf{H}}_{\mathrm{r},k}=\mathrm{diag}\left({\mathbf{h}}_{\mathrm{r},k}^{\mathrm{H}}\right)\mathbf{G}\in {\mathbb{C}}^{N\times M}$

则接收信号$y_k$可以等效表示为
$$y_k=\left({\mathbf{h}}_{\mathrm{d},k}^{\mathrm{H}}+{\mathbf{\theta }}^{\mathrm{H}}{\mathbf{H}}_{\mathrm{r},k}\right)\left(\sum _{k=1}^K{\mathbf{w}}_k{s}_k+{\mathbf{z}}_s\right)+u_k+z_{d,k}$$

第k个用户将来自其他用户的信号（例如:$s_1,\cdots ,s_{k-1},s_{k+1},\cdots ,s_K$）视为干扰，因此，在用户$k$处的$s_k$的译码SINR(信干噪比)表示为

γ k = ∣ ( h d , k H + θ H H r , k ) w k ∣ 2 ∑ i = 1 , i ≠ k K ∣ ( h d , k H + θ H H r , k ) w i ∣ 2 + ( 1 + κ D ) σ 0 2 + ( h d , k H + θ H H r , k ) ( ( 1 + κ D ) κ S diag ⁡ ~ { ∑ k = 1 K w k w k H } + κ D ( ∑ k = 1 K w k ∑ k = 1 K w k H ) ) ( h d , k + H r , k H θ ) . \gamma_{k}=\frac{\left|\left(\mathbf{h}_{\mathrm{d}, k}^{\mathrm{H}}+\boldsymbol{\theta}^{\mathrm{H}} \mathbf{H}_{\mathrm{r}, k}\right) \mathbf{w}_{k}\right|^{2}}{\sum_{i=1, i \neq k}^{K}\left|\left(\mathbf{h}_{\mathrm{d}, k}^{\mathrm{H}}+\boldsymbol{\theta}^{\mathrm{H}} \mathbf{H}_{\mathrm{r}, k}\right) \mathbf{w}_{i}\right|^{2}+\left(1+\kappa_D\right)\sigma_{0}^{2} + \left(\mathbf{h}_{\mathrm{d}, k}^{\mathrm{H}}+\boldsymbol{\theta}^{\mathrm{H}} \mathbf{H}_{\mathrm{r}, k}\right) \left( (1+\kappa_{D})\kappa_{S} \tilde{\operatorname{diag}}\left\{\sum_{k=1}^{K} \mathbf{w}_{k} \mathbf{w}_{k}^{H}\right\} + \kappa_{D} \left( \sum_{k=1}^{K} \mathbf{w}_{k} \sum_{k=1}^{K} \mathbf{w}_{k}^{\mathrm{H}} \right)\right) \left( \mathbf{h}_{\mathrm{d}, k}+\mathbf{H}_{\mathrm{r}, k} ^{\mathrm{H}} \boldsymbol{\theta}\right) } . γk​=∑i=1,i=kK​ ​(hd,kH​+θHHr,k​)wi​ ​2+(1+κD​)σ02​+(hd,kH​+θHHr,k​)((1+κD​)κS​diag~​{∑k=1K​wk​wkH​}+κD​(∑k=1K​wk​∑k=1K​wkH​))(hd,k​+Hr,kH​θ) ​(hd,kH​+θHHr,k​)wk​ ​2​.

此外，AP处的发射功率限制为

$$\sum _{k=1}^K\left(1+{\kappa }_S\right){\Vert {\mathbf{w}}_k\Vert }^2\le P_{\mathrm{T}}$$

综上所述，针对多用户MISO情境下的硬件损伤背景的RIS辅助通信模型如上述(1)、(2)、(3)、(4)、(5)所示。

单用户下的系统模型

考虑RIS辅助的单用户MISO通信系统，建模方式同[@sunshang1],系统中有一个接入基站（Access
Point, AP）与 $1$ 个用户

发送到用户$k$的数据符号简化表示为$s$，是零均值单位方差（功率）的独立随机变量。
对应的发送波束形成向量简化表示为$\mathbf{w}\in {\mathbb{C}}^{M\times 1}$。
与早先[@WSR1][@zhubeidong1]中RIS辅助通信的工作不同，本次毕业设计考虑了实际收发信机硬件损伤（Hardware
Impairments）的影响，信源AP处的发射信号简化表示为：
$$\mathbf{x}=\mathbf{w}s+{\mathbf{z}}_s$$

其中${\mathbf{z}}_s$表示独立于$s$的干扰噪声,表征了功放噪声的共同作用效果，DAC和功放中的非线性，以及示波器的相位噪声，因此${\mathbf{z}}_s$中的元素都是独立零均值高斯随机变量，并且其中第$i$个元素的方差和AP端第$i$个天线处的预期发送信号功率成比例，例如：${\mathbf{z}}_S\sim \mathcal{C}\mathcal{N}\left(0,{\kappa }_S\widetilde{\mathrm{diag}}\left\{\mathbf{w}{\mathbf{w}}^H\right\}\right)$
,其中${\kappa }_S\in \left(0,1\right)$表示发送干扰噪声的归一化方差。

终端处接收到的信号为(隐去(2)中用户k有关量)

$$\begin{array}{rlr}y& =\underset{\text{Direct link }}{{\mathbf{h}}_{\mathrm{d}}^{\mathrm{H}}\mathbf{x}}+\underset{\text{RIS-aided link }}{{\mathbf{h}}_{\mathrm{r}}^{\mathrm{H}}\mathbf{\Theta G}\mathbf{x}}+u+z_d& \\ & =\left({\mathbf{h}}_{\mathrm{d}}^{\mathrm{H}}+{\mathbf{h}}_{\mathrm{r}}^{\mathrm{H}}\mathbf{\Theta G}\right)\left(\mathbf{w}s+{\mathbf{z}}_s\right)+u+z_d& =\tilde{y}+z_d\end{array}$$

$z_d$表示独立于
$\tilde{y}$的终端的接收干扰噪声，它表征了AGC噪声、ADC和AGC中的非线性、示波器相位噪声的联合作用，$z_d$服从零均值高斯分布，$z_d$的方差和无干扰的接收信号成比例，例如：$z_d\sim \mathcal{C}\mathcal{N}\left(0,{\kappa }_D\mathbb{E}\left\{|\tilde{y}{|}^2\right\}\right)$,其中${\kappa }_D\in (0,1)$表示接收干扰噪声的归一化方差

其中，$u\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_0^2\right)$表示第单用户终端接收机处的加性高斯白噪声(AWGN)，为了便于求解上述问题，本次毕设中定义$\mathbf{\theta }={\left[{\theta }_1,\cdots ,{\theta }_N\right]}^{\mathrm{H}}$,并且
${\mathbf{H}}_{\mathrm{r}}=\mathrm{diag}\left({\mathbf{h}}_{\mathrm{r}}^{\mathrm{H}}\right)\mathbf{G}\in {\mathbb{C}}^{N\times M}$

则接收信号$y$可以等效表示为
$$y=\left({\mathbf{h}}_{\mathrm{d}}^{\mathrm{H}}+{\mathbf{\theta }}^{\mathrm{H}}{\mathbf{H}}_{\mathrm{r}}\right)\left(\mathbf{w}s+{\mathbf{z}}_s\right)+u+z_d$$

单用户情况下的接收信噪比为

γ ( w , θ ) = ∣ ( h d H + θ H H r ) w ∣ 2 ( 1 + κ D ) σ 0 2 + ( h d H + θ H H r ) ( ( 1 + κ D ) κ S diag ⁡ ~ { w w H } + κ D ( w w H ) ) ( h d + H r H θ ) . \gamma\left( \mathbf{w},\boldsymbol{\theta}\right)=\frac{\left|\left(\mathbf{h}_{\mathrm{d}}^{\mathrm{H}}+\boldsymbol{\theta}^{\mathrm{H}} \mathbf{H}_{\mathrm{r}}\right) \mathbf{w}\right|^{2}}{\left(1+\kappa_D\right)\sigma_{0}^{2} + \left(\mathbf{h}_{\mathrm{d}}^{\mathrm{H}}+\boldsymbol{\theta}^{\mathrm{H}} \mathbf{H}_{\mathrm{r}}\right) \left( (1+\kappa_{D})\kappa_{S} \tilde{\operatorname{diag}}\left\{ \mathbf{w} \mathbf{w}^{H}\right\} + \kappa_{D} \left( \mathbf{w} \mathbf{w}^{\mathrm{H}} \right)\right) \left( \mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta}\right) } . γ(w,θ)=(1+κD​)σ02​+(hdH​+θHHr​)((1+κD​)κS​diag~​{wwH}+κD​(wwH))(hd​+HrH​θ) ​(hdH​+θHHr​)w ​2​.

此外，AP处的发射功率限制为

$$\left(1+{\kappa }_S\right){\Vert \mathbf{w}\Vert }^2\le P_{\mathrm{T}}$$

由于发端beamforming$\mathbf{w}$同时出现在(9)中SNR表达式的分子和分母，可以估测发射功率很大时信噪比$\gamma \left(\mathbf{w},\mathbf{\theta }\right)$达到饱和。

注意到RIS的反射单元受限于其反射单元相位的量化精度[@fanshe]、[@fanshe2]，为了减少每个RIS单元的计算开销，RIS的反射单元的相位通常是从固定的离散相位值选择，导致不可忽略的相位误差。为了在所提出模型中捕获RIS相位错误的影响，我们把理想的连续相移约束替换为离散约束[@discrete]、[@sunshang1]
${\mathcal{F}}_d\triangleq \left\{{\varphi }_i\mid {\varphi }_i\in \left\{0,\frac{2\pi }{L},\cdots ,\frac{2\pi (L-1)}{L}\right\}\right\}$
其中$L=2^B$表示RIS相移级别的数量，$B$表示用来表征相移级别的比特数。

问题建构

由于多用户问题过于复杂，我们暂且仅考虑单用户问题

在本文中，我们的目的是通过联合优化发送波束形成$w$和IRS反射波束形成矩阵$\mathbf{\theta }$来最大化接受SNR(对于多用户则是SINR)，其中我们对$w$施加了功率约束，对$\mathbf{\theta }$的对角线元素施加了单位模约束。此外由${\mathbf{z}}_s$的分布易推导得知AP的总发射功率为$\left(1+{\kappa }_S\right){\Vert \mathbf{w}\Vert }^2$,此外连续和离散两种相位分布应该同时被使用，并将连续相位分布的结果作为对比，因此我们得到了如下待解决问题，
$$\begin{array}{ll}\underset{\mathbf{w},\mathbf{\theta }}{\mathrm{maximize}}& \gamma (\mathbf{w},\mathbf{\theta })\\ \text{ subject to }& \left(1+{\kappa }_S\right)\Vert \mathbf{w}{\Vert }^2\le P_T\\ & {\theta }_i\in {\mathcal{F}}_1\text{ or }{\mathcal{F}}_2,i=1,\cdots ,N,\end{array}$$

其中$P_T$表示最大信源发射功率，${\theta }_i$是$\mathbf{\theta }$的第$i$个对角元素,${\mathcal{F}}_1\triangleq \left\{{\theta }_i||{\theta }_i\mid =1\right\}$和${\mathcal{F}}_2\triangleq \left\{{\theta }_i\mid {\theta }_i=e^{j{\varphi }_i},{\varphi }_i\in \left\{0,\frac{2\pi }{L},\cdots ,\frac{2\pi (L-1)}{L}\right\}\right\}$

上述问题有极为复杂的目标函数和非凸的单位模约束，很难得到其解析的最优解。尤其是与[@zhubeidong2]中的SNR最大化问题相比，硬件损伤的存在使得波束形成的优化更具挑战。现有方法大多是针对完美硬件的条件下设计的，对于本问题帮助较小。

[@sunshang1]中首先通过广义瑞丽商等方法推导出了发射端AP波束形成的闭式最优解，将[@sunshang1]中的方法使用到本次毕业设计得到AP端的波束形成表示为

w ⋆ = P ~ ( κ D Υ ( θ ) + ( 1 + κ D ) κ S diag ⁡ ~ { Υ ( θ ) } + ( 1 + κ D ) σ n 2 P ~ I M ) − 1 ( h d + H r H θ ) ∥ ( κ D Υ ( θ ) + ( 1 + κ D ) κ S diag ⁡ ~ { Υ ( θ ) } + ( 1 + κ D ) σ n 2 P ~ I M ) − 1 ( h d + H r H θ ) ∥ \mathbf{w}^{\star}=\sqrt{\tilde{P}} \frac{\left(\kappa_{D} \mathbf{\Upsilon}(\boldsymbol{\theta})+\left(1+\kappa_{D}\right) \kappa_{S} \widetilde{\operatorname{diag}}\{\mathbf{\Upsilon}(\boldsymbol{\theta})\}+\frac{\left(1+\kappa_{D}\right) \sigma_{n}^{2}}{\tilde{P}} \mathbf{I}_{M}\right)^{-1}\left( \mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta}\right) }{\left\|\left(\kappa_{D} \boldsymbol{\Upsilon}(\boldsymbol{\theta})+\left(1+\kappa_{D}\right) \kappa_{S} \widetilde{\operatorname{diag}}\{\mathbf{\Upsilon}(\boldsymbol{\theta})\}+\frac{\left(1+\kappa_{D}\right) \sigma_{n}^{2}}{\tilde{P}} \mathbf{I}_{M}\right)^{-1}\left( \mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta}\right) \right\|} w⋆=P~ ​ ​(κD​Υ(θ)+(1+κD​)κS​diag ​{Υ(θ)}+P~(1+κD​)σn2​​IM​)−1(hd​+HrH​θ) ​(κD​Υ(θ)+(1+κD​)κS​diag ​{Υ(θ)}+P~(1+κD​)σn2​​IM​)−1(hd​+HrH​θ)​

简化(12)中较小的量得到其近似如(13)所示：

w ⋆ = P ~ Υ ~ − 1 ( θ ) ( h d + H r H θ ) ∥ Υ ~ − 1 ( θ ) ( h d + H r H θ ) ∥ \mathbf{w}^{\star}=\sqrt{\tilde{P}} \frac{\tilde{\boldsymbol{\Upsilon}}^{-1}(\boldsymbol{\theta})(\mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta})}{\left\|\tilde{\boldsymbol{\Upsilon}}^{-1}(\boldsymbol{\theta})(\mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta})\right\|} w⋆=P~ ​ ​Υ~−1(θ)(hd​+HrH​θ) ​Υ~−1(θ)(hd​+HrH​θ)​

其中：
$${\rm Y}(\mathbf{\theta })=\left({\mathbf{h}}_{\mathrm{d}}+{\mathbf{H}}_{\mathrm{r}}^{\mathrm{H}}\mathbf{\theta }\right)\left({\mathbf{h}}_{\mathrm{d}}^{\mathrm{H}}+{\mathbf{\theta }}^{\mathrm{H}}{\mathbf{H}}_{\mathrm{r}}\right)$$

$$\widetilde{\mathbf{{\rm Y}}}(\mathbf{\theta })\triangleq \left(1+{\kappa }_D\right){\kappa }_S\mathrm{diag}\{\mathbf{{\rm Y}}(\mathbf{\theta })\}+\frac{\left(1+{\kappa }_D\right){\sigma }_n^2}{\tilde{P}}{\mathbf{I}}_M$$
$\tilde{P}=\frac{P_T}{1+{\kappa }_s}$

将(12)代入(11),将(12)中构建的问题转化为问题(14): $$\begin{array}{l}\underset{\theta }{\mathrm{maximize}}\tilde{P}\left({\mathbf{h}}_{\mathrm{d}}+{\mathbf{H}}_{\mathrm{r}}^{\mathrm{H}}\mathbf{\theta }\right){\left({\kappa }_D\mathbf{{\rm Y}}(\mathbf{\theta })+\left(1+{\kappa }_D\right){\kappa }_S\mathrm{diag}\{\mathbf{{\rm Y}}(\mathbf{\theta })\}+\frac{\left(1+{\kappa }_D\right){\sigma }_n^2}{\tilde{P}}{\mathbf{I}}_M\right)}^{-1}\left({\mathbf{h}}_{\mathrm{d}}^{\mathrm{H}}+{\mathbf{\theta }}^{\mathrm{H}}{\mathbf{H}}_{\mathrm{r}}\right)\\ \text{ subject to }\left|{\theta }_i\right|=1,i=1,\cdots ,N\end{array}$$

由于比(11)更复杂的目标函数和非凸约束，问题(14)无法通过求解瑞利商问题来获得最优闭式解，在开题之后的研究中，问题(14)的优化求解是重中之重。文献[@sunshang1]中，首先提出了问题(14)中目标函数的凸的上限并用matlab中的CVX工具求解出，该上限作为对比方案用于评价所提出算法。然后文献[@sunshang1]提出一种基于MM(Majorize-Minimize)的算法以较低复杂度接近所提出上限。

在复现[@sunshang1]所提出方法的基础上，作出改进，或者采用逐次凸逼近(SCA)、分式规划(FP)等方法优化求解(14)中的非凸问题。

创新点和预期研究成果

结合RIS与多天线收发信机硬件损伤的特点，针对单用户(Multiple-Input
Single-Output, MISO)系统收发信机均存在硬件损伤的情况，
提出低复杂度的联合收发信机波束赋形矢量和大规模RIS反射单元系数优化方案，利用计算机仿真验证所提方案的可行性，并比较所提方案与传统无RIS辅助的单用户MISO系统最优传输方案的性能差距

可能的创新点在于：

• 所提出算法对硬件损伤具有更强的鲁棒性

• 所提出算法有更大的性能增益与更低的复杂度

• 所提出方案与现有方案相比更好地发掘了IRS辅助通信以及硬件损伤的场景的潜在价值

具体性能指标要求:

输入条件：

• 发射机天线数：$4\sim 8$；

• 接收机天线数：$4\sim 8$；

• RIS反射单元数：$30\sim 100$；

功能和性能指标要求：

• 相较于无RIS辅助通信场景, RIS辅助通信的MSE性能提升不小于3dB；

• 相较于忽略系统硬件损伤的方案，所提方案的MSE性能提升不小于5dB；

Beamforming Optimization for IRS-Aided Communications With Transceiver Hardware Impairments 的复现仿真

对矩阵$t$取模值也就得到了AP的信号发送功率$\Vert \mathbf{t}{\Vert }^2=\Vert \mathbf{w}x{\Vert }^2+\Vert {\mathbf{z}}_{\mathbf{S}}{\Vert }^2$

$$\left(1+{\kappa }_S\right)\Vert \mathbf{w}{\Vert }^2\le P_{T}orP$$

$${\mathbf{z}}_S\sim \mathcal{C}\mathcal{N}\left(0,{\kappa }_S\widetilde{\mathrm{diag}}\left\{\mathbf{w}{\mathbf{w}}^H\right\}\right)$$

$P=12dBW$

w ⋆ = P ~ ( κ D Υ ( θ ) + ( 1 + κ D ) κ S diag ⁡ ~ { Υ ( θ ) } + ( 1 + κ D ) σ n 2 P ~ I M ) − 1 ( h d + H r H θ ) ∥ ( κ D Υ ( θ ) + ( 1 + κ D ) κ S diag ⁡ ~ { Υ ( θ ) } + ( 1 + κ D ) σ n 2 P ~ I M ) − 1 ( h d + H r H θ ) ∥ \mathbf{w}^{\star}=\sqrt{\tilde{P}} \frac{\left(\kappa_{D} \mathbf{\Upsilon}(\boldsymbol{\theta})+\left(1+\kappa_{D}\right) \kappa_{S} \widetilde{\operatorname{diag}}\{\mathbf{\Upsilon}(\boldsymbol{\theta})\}+\frac{\left(1+\kappa_{D}\right) \sigma_{n}^{2}}{\tilde{P}} \mathbf{I}_{M}\right)^{-1}\left( \mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta}\right) }{\left\|\left(\kappa_{D} \boldsymbol{\Upsilon}(\boldsymbol{\theta})+\left(1+\kappa_{D}\right) \kappa_{S} \widetilde{\operatorname{diag}}\{\mathbf{\Upsilon}(\boldsymbol{\theta})\}+\frac{\left(1+\kappa_{D}\right) \sigma_{n}^{2}}{\tilde{P}} \mathbf{I}_{M}\right)^{-1}\left( \mathbf{h}_{\mathrm{d}}+\mathbf{H}_{\mathrm{r}} ^{\mathrm{H}} \boldsymbol{\theta}\right) \right\|} w⋆=P~ ​ ​(κD​Υ(θ)+(1+κD​)κS​diag ​{Υ(θ)}+P~(1+κD​)σn2​​IM​)−1(hd​+HrH​θ) ​(κD​Υ(θ)+(1+κD​)κS​diag ​{Υ(θ)}+P~(1+κD​)σn2​​IM​)−1(hd​+HrH​θ)​

$\Vert {\mathbf{w}}^{\star }\Vert =\sqrt{\tilde{P}}$

对CVX求出来的最优解取范数，求SNR

广义瑞利商的简单学习

【线性代数】瑞利商和广义瑞利商
https://segmentfault.com/a/1190000038228479

参考文献

C. Liaskos, S. Nie, A. Tsioliaridou, A. Pitsillides, S. Ioannidis, and
I. Akyildiz, “A new wireless communication paradigm through
software-controlled metasurfaces,” IEEE Commun. Mag., vol. 56, no. 9,
pp. 162–169, Sep. 2018.

E. Basar, M. D. Renzo, J. D. Rosny, M. Debbah, M. Alouini, and R. Zhang,
“Wireless communications through reconfifigurable intelligent surfaces,”
IEEE Access, vol. 7, pp. 116 753–116 773, 2019.

Zhao J. A survey of intelligent reflecting surfaces (IRSs): Towards 6G
wireless communication networks[J]. arXiv preprint arXiv:1907.04789,
2019.

Wu Q, Zhang R. Towards smart and reconfigurable environment: Intelligent
reflecting surface aided wireless network[J]. IEEE Communications
Magazine, 2019, 58(1): 106-112.

T. L. Marzetta, “Noncooperative cellular wireless with unlimited num-
bers of base station antennas,” IEEE Trans. Wireless Commun.,vol.9, no.
11, pp. 3590–3600, Nov. 2010. F. Rusek, D. Persson, B. K. Lau, E. G.
Larsson, T. L. Marzetta, and F. Tufvesson, “Scaling up MIMO:
Opportunities and challenges with very large arrays,” IEEE Signal
Process. Mag., vol. 30, no. 1, pp. 40–60, Jan. 2013.

Q. Wu and R. Zhang, “Intelligent reflecting surface enhanced wireless
network: Joint active and passive beamforming design,” in Proc. IEEE
Global Commun. Conf. (GLOBECOM), Abu Dhabi, UAE, Dec. 2018, pp. 1–6.

Q. Wu and R. Zhang, “Beamforming optimization for intelligent reflecting
surface with discrete phase shifts,” in Proc. IEEE Int. Conf. Acoust.,
Speech Signal Process. (ICASSP), Brighton, U.K., May 2019, pp.
7830–7833.

Wu Q, Zhang R. Intelligent reflecting surface enhanced wireless network
via joint active and passive beamforming[J]. IEEE Transactions on
Wireless Communications, 2019, 18(11): 5394-5409.

Q. Wu and R. Zhang, “Beamforming optimization for wireless network aided
by intelligent reflecting surface with discrete phase shifts,” IEEE
Trans. Commun., vol. 68, no. 3, pp. 1838–1851, Mar. 2020.

C. Huang, A. Zappone, M. Debbah, and C. Yuen, “Achievable rate maxi-
mization by passive intelligent mirrors,” in Proc. IEEE Int. Conf.
Acoust., Speech Signal Process. (ICASSP), Calgary, AB, Canada, Apr.
2018, pp. 1–5.

Guo H, Liang Y C, Chen J, et al. Weighted sum-rate maximization for
reconfigurable intelligent surface aided wireless networks[J]. IEEE
Transactions on Wireless Communications, 2020, 19(5): 3064-3076.

Wang S, Li Q, Wu S X, et al. Sum rate maximization for multiuser MISO
downlink with intelligent reflecting surface[J]. arXiv preprint
arXiv:1912.09315, 2019.

C. Huang, A. Zappone, G. C. Alexandropoulos, M. Debbah, and C. Yuen,
“Reconfigurable intelligent surfaces for energy efficiency in wireless
communication,” IEEE Trans. Wireless Commun., vol. 18, no. 8, pp.
4157–4170, Aug. 2019.

C. Huang, G. C. Alexandropoulos, A. Zappone, M. Debbah, and C. Yuen,
“Energy efficient multi-user MISO communication using low resolution
large intelligent surfaces,” in Proc. IEEE Globecom Work- shops (GC
Wkshps), Abu Dhabi, UAE, Dec. 2018, pp. 1–6.

H. Shen, W. Xu, S. Gong, Z. He, and C. Zhao, “Secrecy rate maximization
for intelligent reflecting surface assisted multi-antenna
communications,” IEEE Commun. Lett., vol. 23, no. 9, pp. 1488–1492,
Sep. 2019.

X. Yu, D. Xu, and R. Schober, “Enabling secure wireless communica- tions
via intelligent reflecting surfaces,” in Proc. IEEE Global Commun. Conf.
(GLOBECOM), Waikoloa, HI, USA, Dec. 2019, pp. 1–6.

M. Cui, G. Zhang, and R. Zhang, “Secure wireless communication via
intelligent reflecting surface,” IEEE Wireless Commun. Lett.,vol.8, no.
5, pp. 1410–1414, Oct. 2019.

X. Guan, Q. Wu, and R. Zhang, “Intelligent reflecting surface assisted
secrecy communication: Is artificial noise helpful or not?” IEEEWireless
Commun. Lett., vol. 9, no. 6, pp. 778–782, Jun. 2020.

X. Yu, D. Xu, Y. Sun, D. W. K. Ng, and R. Schober, “Robust and secure
wireless communications via intelligent reflecting sur- faces,” IEEE J.
Sel. Areas Commun., vol. 38, no. 11, pp. 2637–2652, Nov. 2020.

S. Gong, C. Xing, X. Zhao, S. Ma and J. An. Unified IRS-Aided MIMO
Transceiver Designs via Majorization Theory[J]. IEEE Transactions on
Signal Processing, 2021, 69: 3016-3032.

Q. Wu and R. Zhang, “Weighted sum power maximization for intelligent
reflecting surface aided SWIPT,” IEEE Wireless Commun. Lett.,vol. 9, no.
5, pp. 586–590, May 2020.

H. Suzuki, T. Van Anh Tran, I. B. Collings, G. Daniels, and M. Hedley,
“Transmitter noise effect on the performance of a MIMO-OFDM hard- ware
implementation achieving improved coverage,” IEEE J. Sel. Areas Commun.,
vol. 26, no. 6, pp. 867–876, Aug. 2008.

W. Namgoong, “Modeling and analysis of nonlinearities and mismatches in
AC-coupled direct-conversion receiver,” IEEE Trans. Wireless Com- mun.,
vol. 4, no. 1, pp. 163–173, Jan. 2005.

E. Bjornson, P. Zetterberg, M. Bengtsson, and B. Ottersten, “Capac- ity
limits and multiplexing gains of MIMO channels with trans- ceiver
impairments,” IEEE Commun. Lett., vol. 17, no. 1, pp. 91–94, Jan. 2013.

E. Bjornson, J. Hoydis, M. Kountouris, and M. Debbah, “Massive MIMO
systems with non-ideal hardware: Energy efficiency, estima- tion, and
capacity limits,” IEEE Trans. Inf. Theory, vol. 60, no. 11, pp.
7112–7139, Nov. 2014.

J. Zhu, D. W. K. Ng, N. Wang, R. Schober, and V. K. Bhargava, “Analysis
and design of secure massive MIMO systems in the presence of hardware
impairments,” IEEE Trans. Wireless Commun., vol. 16, no. 3, pp.
2001–2016, Mar. 2017.

H. Shen, W. Xu, S. Gong, C. Zhao and D. W. K. Ng. Beamforming
Optimization for IRS-Aided Communications With Transceiver Hardware
Impairments[J]. IEEE Transactions on Communications, 2020, 69(2):
1214-1227.

E. Bjornson, P. Zetterberg, and M. Bengtsson, “Optimal coordinated
beamforming in the multicell downlink with transceiver impairments,” in
Proc. IEEE Global Commun. Conf. (GLOBECOM), Anaheim, CA, USA, Dec. 2012,
pp. 4775–4780.

J. You, E. Liu, R. Wang, and W. Su, “Joint source and relay pre- coding
design for MIMO two-way relay systems with transceiver impairments,”
IEEE Commun. Lett., vol. 21, no. 3, pp. 572–575, Mar. 2017.

H. Shen, C. Liu, W. Xu, and C. Zhao, “Optimized full-duplex MIMO DF
relaying with limited dynamic range,” IEEE Access,vol.5, pp.
20726–20735, 2017.

O. Taghizadeh, A. C. Cirik, and R. Mathar, “Hardware impair- ments aware
transceiver design for full-duplex amplify-and-forward MIMO relaying,”
IEEE Trans. Wireless Commun., vol. 17, no. 3, pp. 1644–1659, Mar. 2018.

L. Godara, “The effect of phase-shifter errors on the performance of an
antenna-array beamformer,” IEEE J. Ocean. Eng., vol. OE-10, no. 3, pp.
278–284, Jul. 1985.

B. Peng, S. Priebe, and T. Kurner, “Effects of phase shift errors on the
antenna directivity of phased arrays in indoor terahertz communi-
cations,” in Proc. 11th Int. Symp. Wireless Commun. Syst. (ISWCS),
Barcelona, Spain, Aug. 2014, pp. 355–359.

Q. Wu and R. Zhang, “Beamforming optimization for intelligent reflecting
surface with discrete phase shifts,” in Proc. IEEE Int. Conf. Acoust.,
Speech Signal Process. (ICASSP), Brighton, U.K., May 2019,

pp. 7830–7833.

Zhou G, Pan C, Ren H, et al. Secure wireless communication in RIS-aided
MISO system with hardware impairments[J]. IEEE Wireless Communications
Letters, 2021, 10(6): 1309-1313.

Han Y, Tang W, Jin S, et al. Large intelligent surface-assisted wireless
communication exploiting statistical CSI[J]. IEEE Transactions on
Vehicular Technology, 2019, 68(8): 8238-8242.

Sun Y, Babu P, Palomar D P. Majorization-minimization algorithms in
signal processing, communications, and machine learning[J]. IEEE
Transactions on Signal Processing, 2016, 65(3): 794-816.
:::
eless Communications
Letters, 2021, 10(6): 1309-1313.

Han Y, Tang W, Jin S, et al. Large intelligent surface-assisted wireless
communication exploiting statistical CSI[J]. IEEE Transactions on
Vehicular Technology, 2019, 68(8): 8238-8242.

Sun Y, Babu P, Palomar D P. Majorization-minimization algorithms in
signal processing, communications, and machine learning[J]. IEEE
Transactions on Signal Processing, 2016, 65(3): 794-816.
:::