Deep shape-aware descriptor论文笔记
说明:
1.此乃本人阅读论文过程中所记录的笔记,由于本人水平有限,难免会出现遗漏重点或表述不清等问题,请各位见谅。同时希望各位指出我的问题,让我发现问题所在,谢谢大家Thanks♪(・ω・)ノ。
2.有些用词根据原文翻译(或是直接用原文),可能语句不通畅。(毕竟我是一个六级考了五次的憨憨)
3.数据处理部分和结论分析部分没有加入,此处主要为了理清文章描述方法的处理流程。
1.重要概念介绍
拉普拉斯-贝尔特拉米算子(Laplace-Beltrami operator,LBO):
给定紧凑的黎曼流形 M \mathbb{M} M,空间 L 2 ( M ) L^2(\mathbb{M}) L2(M)是包含所有光滑且平方可积函数的希尔伯特空间,其内积定义为 < f 1 , f 2 > = ∫ M f 1 ( x ) f 2 ( x ) d a ( x )
Δ M f = − d i v ( ∇ M f ) \Delta_{\mathbb{M}}f=-div(\nabla_{\mathbb{M}}f) ΔMf=−div(∇Mf)
拉普拉斯-贝尔特拉米算子为线性半正定算子,将拉普拉斯算子推广到非欧氏空间。
将其进行离散化。定义实函数 f : V → R f:\mathbb{V}\rightarrow\mathbb{R} f:V→R,其中 V \mathbb{V} V表示网格顶点的集合,给出m维向量f=(f(i)),其中第i个分量表示网格的第i个顶点处的函数值。利用有限元法或者有限体素法,在顶点 v i v_i vi处 Δ M f \Delta_{\mathbb{M}}f ΔMf的值可由下式逼近:
Δ M f ≈ 1 a i ∑ j ∼ i c o t α i j + c o t β i j 2 ( f ( i ) − f ( j ) ) \Delta_{\mathbb{M}}f\approx\frac{1}{a_i}\sum_{j\sim i}\frac{cot\alpha_{ij}+cot\beta_{ij}}{2}(f(i)-f(j)) ΔMf≈ai1∑j∼i2cotαij+cotβij(f(i)−f(j))
其中 α i j \alpha_{ij} αij和 β i j \beta_{ij} βij分别表示 ∠ ( v i v k 1 v j ) \angle(v_iv_{k_1}v_j) ∠(vivk1vj)和 ∠ ( v i v k 2 v j ) \angle(v_iv_{k_2}v_j) ∠(vivk2vj),对应的面 t α = { v i , v k 1 , v j } t^\alpha=\{v_i,v_{k_1},v_j\} tα={vi,vk1,vj}和 t α = { v i , v k 2 , v j } t^\alpha=\{v_i,v_{k_2},v_j\} tα={vi,vk2,vj},两个面邻接于边[i,j], a i a_i ai表示顶点i处的Voronoi单元的面积。
使用谱分析方法,用m×m阶矩阵 L = D − 1 E L=D^{-1}E L=D−1E,其中D=diag( d i d_i di))为正定对角矩阵, d i d_i di表示顶点i处的Voronoi单元的面积。 E = d i a g ( ∑ k ≠ i c i k ) − ( c i j ) E=diag(\sum_{k\neq i}c_{ik})-(c_{ij}) E=diag(∑k=icik)−(cij)为稀疏对称矩阵,权重 c i j c_{ij} cij由如下公式给出
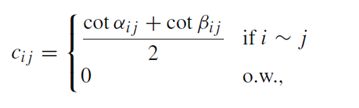
利用特征值方程 E φ ℓ = λ ℓ D φ ℓ E\varphi_\ell=\lambda_\ell D \varphi_\ell Eφℓ=λℓDφℓ求L的特征值 λ ℓ \lambda_\ell λℓ和特征向量 φ ℓ \varphi_\ell φℓ,对特征值进行升序排序,给出相应的正交特征向量,其中特征向量的正交性由如下D内积定义:
< φ k , φ ℓ > = ∑ i = 1 m d i φ k ( i ) φ ℓ ( i ) = δ k ℓ , <\varphi_k,\varphi_\ell>=\sum_{i=1}^{m}d_{i}\varphi_k(i)\varphi_\ell(i)=\delta_{k\ell}, <φk,φℓ>=∑i=1mdiφk(i)φℓ(i)=δkℓ, ∀ k , ℓ = 1 , . . . , m \forall k,\ell=1,...,m ∀k,ℓ=1,...,m
深度自编码器(Deep auto-encoders):
一种用于重构输入作为输出的神经网络,它使用随机梯度下降的反向传播算法从无标签集中学习特征。如下图所示,一个自编码器包含一个编码器和解码器。

将编码器记作 f θ f_\theta fθ,它将输入向量 x ∈ R d x\in\mathbb{R}^d x∈Rd映射成隐藏层表示 a ∈ R d a\in\mathbb{R}^d a∈Rd,
a = f θ ( x ) = σ ( W x + b ) a = f_\theta(x)=\sigma(Wx+b) a=fθ(x)=σ(Wx+b)
记θ={W,b},其中W∈ R r × d \mathbb{R}^{r\times d} Rr×d和 b ′ ∈ R d b^{'}\in\mathbb{R}^d b′∈Rd为编码器的权重矩阵和偏移向量,σ为非线性激活函数。
将解码器记作 g θ ′ g_{\theta^{'}} gθ′,它将隐藏层表示h映射为输入x的重构 x ^ \hat{x} x^,
x ^ = g θ ′ ( a ) = σ ( W ′ a + b ′ ) \hat{x}=g_{\theta^{'}}(a)=\sigma(W^{'}a+b^{'}) x^=gθ′(a)=σ(W′a+b′)
记 θ ′ = { W ′ , b ′ } . \theta^{'}=\{W^{'},b^{'}\}. θ′={W′,b′}.其中 W ′ ∈ R d × r W^{'}\in\mathbb{R}^{d\times r} W′∈Rd×r和 b ′ ∈ R d b^{'}\in\mathbb{R}^d b′∈Rd为解码器的权重矩阵和偏移向量。其中W和 W ′ W^{'} W′。
由此得到如下最小化目标函数(为了防止数据过拟合,我们加入正则化分量):
£ ( W , b , b ′ ) = 1 2 ∑ i = 1 N ∥ x i − x i ^ ∥ 2 2 + λ 2 ∥ W ∥ F 2 \pounds(W,b,b^{'})=\frac{1}{2}\sum_{i=1}^{N}\|x_i-\hat{x_i}\|_2^2+\frac{\lambda}{2}\|W\|_F^2 £(W,b,b′)=21∑i=1N∥xi−xi^∥22+2λ∥W∥F2
2.解决的问题
从三维模型中获取简洁、几何信息丰富且计算效率高的深度模型感知描述符。
3.处理方法主要步骤
整个处理流程如下图所示:
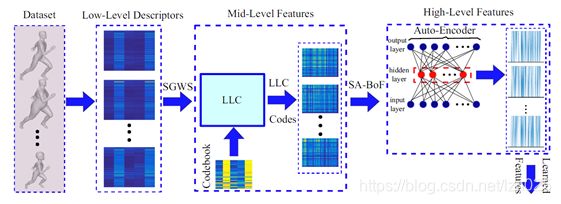
(1) 低层特征(Low-Level Descriptors)
用谱图小波特征(Spectral Graph Wavelets Signature,SGWS)矩阵生成三维模型的局部描述符。对于给定的解决半径R,顶点j处的SGWS是一个p维向量,如下定义
s j = { s Q ( j ) ∣ Q = 1 , . . . , R } s_j=\{s_Q(j)|Q=1,...,R\} sj={sQ(j)∣Q=1,...,R}
其中 s Q ( j ) s_Q(j) sQ(j)是顶点j处的模型描述符,解决层Q由下式给出
s Q ( j ) = { W δ j ( t q , j ) ∣ q = 1 , . . . , Q } ∪ { S δ j ( j ) } s_Q(j)=\{W_{\delta_{j}}(t_{q},j)|q=1,...,Q\}\cup\{S_{\delta_{j}(j)}\} sQ(j)={Wδj(tq,j)∣q=1,...,Q}∪{Sδj(j)}
在每个解决层Q,顶点j处的描述符 s Q ( j ) s_Q(j) sQ(j)是一个(Q+1)维向量,由谱图小波系数 W δ j ( t q , j ) W_{\delta_{j}}(t_{q},j) Wδj(tq,j)和尺度函数系数 S δ j ( j ) S_{\delta_{j}(j)} Sδj(j),它们定义如下
W δ j ( t q , j ) = ∑ ℓ = 1 m a j 2 g ( t q λ ℓ ) φ ℓ 2 ( j ) , W_{\delta_{j}}(t_{q},j)=\sum_{\ell=1}^{m}a_{j}^{2}g(t_q\lambda_\ell)\varphi_{\ell}^{2}(j), Wδj(tq,j)=∑ℓ=1maj2g(tqλℓ)φℓ2(j), q=1,…,Q
S δ j ( j ) = ∑ ℓ = 1 m a j 2 h ( λ ℓ ) φ ℓ 2 ( j ) S_{\delta_{j}(j)}=\sum_{\ell=1}^{m}a_{j}^{2}h(\lambda_{\ell})\varphi_{\ell}^{2}(j) Sδj(j)=∑ℓ=1maj2h(λℓ)φℓ2(j)
其中g和h分别是谱图小波生成内核和尺度函数。谱图小波生成内核g视作带通滤波器,尺度函数h视作低通滤波器,以此编码网格顶点上的函数低频部分。小波尺度 t q ( t q > t q + 1 ) t_q(t_q>t_{q+1}) tq(tq>tq+1)在最大尺度 t 1 t_1 t1和最小尺度 t Q t_Q tQ之间在对数下等距选取。 s j s_j sj的维数p由以下公式确定
p = ( R + 1 ) ( R + 2 ) 2 − 1 p=\frac{(R+1)(R+2)}{2}-1 p=2(R+1)(R+2)−1
接下来定义谱图小波特征矩阵 S = ( s 1 , … , s m ) ∈ R p × m S=(s_1,…,s_m)∈R^{p×m} S=(s1,…,sm)∈Rp×m,其中 s i s_i si是顶点i的特征,m是网格顶点数目。在该论文中使用了下列三次样条小波函数g和尺度函数h
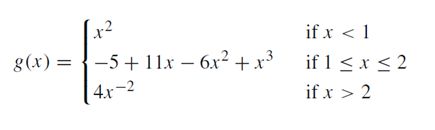
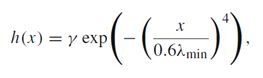
其中 λ m i n = λ m a x / 20 λ_min=λ_max/20 λmin=λmax/20, γ \gamma γ设置为使h(0)等于g的最大值。最大尺度和最小尺度分别设置为 t 1 = 2 / λ m i n t_1=2/λ_{min} t1=2/λmin和 t Q = 2 / λ m a x t_Q=2/λ_{max} tQ=2/λmax。
(2)中层特征(Mid-level features)
对低层特征应用BoF(Bag of Feature,特征袋)框架构造中间特征。
BoF包含以下四个主要步骤:
特征提取和描述(Feature extraction and description):在BoF范式中,一个三维模型 M \mathbb{M} M被视作m个具有相同维数p的局部描述符的集合,其中不同特征向量的阶数不重要。局部描述符分为稠密和稀疏两类,稠密描述符对网格的每个顶点进行计算,稀疏描述符只在有特征检测算法得到的关键点处进行计算。
码书设计(Codebook design):应用K均值算法构建离线字典,得到具有代表性的局部描述符的集合。此处使用内在空间分割算法选取具有代表性的描述符,确保每个模型的每个分割参与生成过程。最后用p×k字典矩阵 V = ( v 1 , … , v k ) V=(v_1,…,v_k) V=(v1,…,vk),其中p维向量 v i v_i vi维聚类中心。
特征编码(Feature coding):使用局部约束线性编码(Locality-constrained Linear Coding,LLC)的方式完成。LLC码 u i u_i ui由以下正则化最小二乘法得到
u i = a r g min 1 T u i = 1 ∥ s i − V u i ∥ 2 2 + λ ∥ d i ⨀ u i ∥ 2 2 u_i=arg \min\limits_{1^Tu_i=1}\|s_i-Vu_i\|_2^2+\lambda\|d_i\bigodot u_{i}\|_2^2 ui=arg1Tui=1min∥si−Vui∥22+λ∥di⨀ui∥22
其中⨀表示数组元素依次相乘, d i = e x p ( d i s t ( s i , V ) δ ) d_i=exp(\frac{dist(s_i,V)}δ) di=exp(δdist(si,V))度量第i个描述符和所有码字的相似度, δ \delta δ用于调整局部适配器的权重衰减速度。(其中 d i s t ( s i , V ) = ( ‖ s i − v 1 ‖ 2 , … , ‖ s i − v k ‖ 2 ) dist(s_i,V)=(‖s_i-v_1 ‖_2,…,‖s_i-v_k ‖_2) dist(si,V)=(‖si−v1‖2,…,‖si−vk‖2))
由此产生k×m的LLC编码矩阵 U = ( u 1 , … , u m ) 。 U=(u_1,…,u_m)。 U=(u1,…,um)。
特征池化(Feature pooling):将前一步得到的结果绘制成直方图h
h = U 1 m = ( h r ) r = 1 , . . , k h=U1_m=(h_r)_{r=1,..,k} h=U1m=(hr)r=1,..,k
其中 h r = ∑ i = 1 m u r i h_r=\sum_{i=1}^mu_{ri} hr=∑i=1muri。
然后由h=P(U)给出特征向量h,其中P为预定义的池化函数,将不同码字的信息汇聚在一个向量中。
引入双调和距离(biharmonic distance)来度量BoF向量间的空间关系。用k×k矩阵F来定义三维模型的深度感知描述符
F = U K U T F=UKU^T F=UKUT
其中U为LLC编码矩阵, K = ( k i j ) K=(k_{ij}) K=(kij)为m×m阶双调和距离内核矩阵,由LBO算子的特征值和特征向量定义
κ_{ij}=\sum_{\ell=1}m\frac{1}{\lambda_{\ell}{2}}(\varphi_{\ell}(i)-\varphi_{\ell}(j))^2
对于每个三维模型,用F表示它的中层特征,其包含全局描述符。
(3)高层特征(High-level features)
将中层特征作为输入,用深度自编码器学习高级特征。高层特征从深度自编码器的最后一个隐藏层的输出提取,生成r_L维高层特征向量a_L,其中r_L为最后一个隐藏层的神经元数量。
4.特点
(1)用谱图小波描述低层模型描述符。
(2)用BoF框架构造中层特征,使用LLC完成特征编码,并引入双调和距离来度量BoF向量间的空间关系。
(3)实现了一种可用于学习高级特征的自动编码器,可用于三维模型检索任务的深度模型描述符。