408王道数据结构强化——应用题

目录

1.栈、数组和队列的应用

1.1.栈

1.1.1.栈的定义：

1.1.2.栈的基本操作的代码实现：

1.1.3.栈的数据结构的手绘

​编辑

1.1.4.栈的基本操作的手绘

1.2.队列

1.2.1.队列的定义

1.2.2.顺序队列的基本操作（循环队列）

1.2.3.链式队列的基本操作

1.2.4.队列的数据结构的手绘

1.2.5.队列的基本操作的手绘

1.3.数组

2.树

2.1.树的数据结构定义和手绘

2.1.1.二叉树

2.1.2.多叉树

2.2.二叉树的基本操作

2.3.哈夫曼树

2.4.并查集

2.5.二叉查找树

2.6.平衡二叉树

3.图

3.1.最小生成树（Prim和Kruskal）

3.2.最短路径（Dijkstra和Flyod）

3.3.有向无环图

3.3.1.描述算式

3.3.2.拓扑排序

3.3.3.关键路径

3.4.图的数据结构

4.查找

4.1.顺序查找

4.2.折半查找

4.3.分块查找

4.4.二叉搜索树和二叉排序树

4.5.散列表

4.6.kmp算法

5.排序

---

1.栈、数组和队列的应用

1.1.栈

1.1.1.栈的定义：

#define MAXSIZE
typedef struct Stack{
    int data[MAXSIZE];
    int top;
}Stack;

1.1.2.栈的基本操作的代码实现：

1.建立栈：

void InitStack(Stack &s){
    s.top = -1;
}

2.入栈（push）：

bool Push(Stack &s, int e){
    if (s.top == MAXSIZE - 1) return false;    //判断是否栈已满
    s.data[++s.top] = e;    //将栈顶指针先+1，然后将e存入栈顶
    return true;
}

3.出栈（pop）：

bool Pop(Stack &s, int &e){
    if (s.top == -1) return false;    //判断是否栈空
    s.data[s.top--] = e;    //先将栈顶元素赋值给e，然后栈顶指针-1
    return true;
}

4.判断栈空：

bool IsEmpty(Stack s){
    if (s.top == -1) return true;    //判断栈顶指针是否为-1
    else return false;
}

5.查看栈顶元素：

bool GetTop(Stack S, int &e){
    if (s.top == -1) return false;    //判断是否栈空
    e =  s.data[s.top];
    return true;
}

1.1.3.栈的数据结构的手绘

1.1.4.栈的基本操作的手绘

1.2.队列

1.2.1.队列的定义

1.顺序栈：

#define MAXSIZE 100
typedef struct SqQueue{
    int data[MAXSIZE];
    int front, rear;
}SqQueue;

2.链栈：

typedef struct LNode{    //链式队列结点的定义
    struct LNode *next;
    int data;
}*LinkList, LNode;

typedef struct LinkQueue{    //链式队列的定义
    LNode *front, *rear;    //头尾指针
}LinkQueue;

1.2.2.顺序队列的基本操作（循环队列）

1.建立队列：

void InitQueue(SqQueue &Q){
    Q.rear = 0;    //将front和rear都置为0,
    Q.front = 0;
}

2.入队：rear对队列的最大容量取余，且不能使用Q.rear++

bool EnQueue(SqQueue &Q, int e){
    if ((Q.rear + 1)) % MAXSIZE = Q.front) return false;    //判断是否队满
    Q.data[Q.rear] = e;
    Q.rear = (Q.rear + 1) % MAXSIZE;
    return true;
}

3.出队：front对队列的最大容量取余，且不能使用Q.front++

bool DeQueue(SqQueue &Q, int &e){
    if (Q.front == Q.rear) return false;    //队空
    e = Q.data[Q.front++];
    return true;
}

4.判断对空：

bool IsEmpty(SqQueue Q){
    if (Q.front == Q.rear) return true;    //队空时rear和front指向同一个地方
    else return false;
}

5.得到队首元素：

bool GetFront(SqQueue Q, int &e){
    if (Q.front == Q.rerar) return false;    //队空
    e = Q.data[Q.front];
    return true;
}

1.2.3.链式队列的基本操作

1.队列初始化：在申明一个链式队列后，只有头尾结点指针，需要申明一个头结点

void InitQueue(LinkQueue &Q){
    Q.front = Q.rear = (LNode*)malloc(sizeof(LNode));    //申明一个头结点
    Q.front->next = NULL;    //将next指针置空
}

2.入队：

void EnQueue(LinkQueue &Q, int e){
    LNode *p = (LNode*)malloc(sizeof(LNode));    //申明一个新结点p
    p->data = e;    //e赋值给p的数据域
    p->next = NULL;    //p的next指针置空
    Q.rear->next = p;    //将p插入到队尾
    Q.rear = p;    //将rear指向p
}  

3.出队：需要判断是否队中只有一个元素

bool DeQueue(LinkQueue &Q, int &e){
    if (Q.rear == Q.front) return false;    //队空
    LNode *p = Q.front->next;    //申明LNode类型的指针p指向队首元素
    e = p->data;    //将p的数据域赋值给e
    if (Q.rear = p) {    //队中只有元素p
        Q.rear = Q.front;
        Q.front->next;
    }
    else Q.front->next = p->next;    //对中不止有元素p，则front的next指针指向p的下一个元素
    free(p);    
    return true;
}

4.判断对空：队首指针和队尾指针指向同一个地方时对空

bool IsEmpty(LinkQueue Q){
    if (Q.front == Q.rear) return true;
    else return false;
}

1.2.4.队列的数据结构的手绘

1.2.5.队列的基本操作的手绘

1.循环队列：

2.链式队列：

①front指针始终指向头结点，rear在队中有元素时始终指向队尾元素

②初始状态和队空时：front和rear都只指向头结点

1.3.数组

申明n个元素的数组：

int *arr = (int*)malloc(sizeof(int) * n);
memset(arr, 0, sizeof(int) * n);

2.树

2.1.树的数据结构定义和手绘

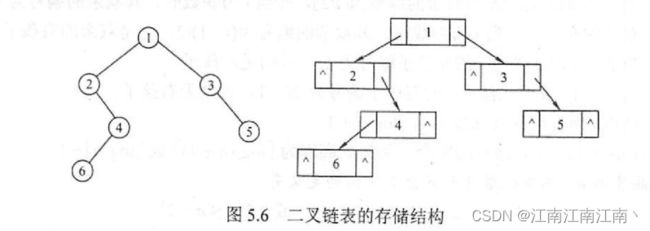
2.1.1.二叉树

1.顺序结构：通常用于存放完全二叉树

#define MAXSIZE 100
typedef struct TreeNode{
    int value;    //当前结点的值
    bool IsEmpty;    //表示当前的结点是否为空
}TreeNode;

 2.单向链：

typedef struct BiTNode{
    int value;    //当前结点的值
    struct BiTNode *lchild, *rchild;    //指向当前结点左右子树的指针
}BiTNode, *BiTree;

 3.双向链：双亲节点指向孩子结点，孩子结点也指向双亲结点

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild, *parent;    //parent指针指向该结点的双亲结点
    int value;
}BiTNode, *BiTree;

2.1.2.多叉树

408数据结构学习笔记——树、森林_江南江南江南丶的博客-CSDN博客

1.双亲表示法（并查集）

#define MAXSIZE 100

typedef struct PNode{
    int value;    //该结点的值
    int parent;    //伪指针，用于指向双亲结点（双亲结点的数组下标）
}PNode;

typedef struct PTree{
    PNode node[MAXSIZE];    //申明一片PNode类型个数为MAXSIZE的数组用于存储树
    int n;    //表示该树中的结点个数
}PTree;

2.孩子表示法：

typedef struct CTNode{    //链式存储，存放该结点的每个孩子结点的信息（非孩子结点的数据）
    int child;    //该结点的孩子结点在数组中的下标
    struct CTNode *next;    //指向该孩子结点的下个孩子结点
}CTNode;

typedef struct CTBox{    //定义具体结点，存放结点数据，并且存放该元素的第一个孩子结点
    int data;
    CTNode *firstChild;
}CTBox;

typedef struct CTree{    //顺序存储结点
    CTBox nodes[MAXSIZE];    //定义一个CTBox类型长度为MAXSIZE的数组
    int n, r;    //n为结点的总个数，r为根节点的数组下标
}CTree;
    

3.孩子兄弟表示法：

typedef struct CSNode {
    int value;    //结点数据
    struct CSNode *firstChild, *nextChild;
}CSNode, *CSTree;

2.2.二叉树的基本操作

408数据结构学习笔记——二叉树的遍历和线索二叉树_江南江南江南丶的博客-CSDN博客

1.先序遍历：

void PreOrder(BiTree T){
    if (T) {
        visit(T);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

2.中序遍历：

void InOrder(BiTree T) {
    if (T) {
        InOrder(T->lchild);
        visit(T);
        InOrder(T->rchild);
    }
}

3.后序遍历：

void PostOrder(BiTree T) {
    if (T）{
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        visit(T);
    }
}

4.层次遍历：

typedef struct BiTNode{
    int value;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

typdef struct LinkNode{
    BiTNode *data;
    struct LinkNode *next;
}LinkNode;

typdef struct LinkQueue{
    LinkNode *front, *rear;
}LinkQueue;

void LevelOrder(BiTree T) {
    LinkQueue Q;
    InitQueue(Q);    //初始化队列
    BiTNode *p;
    EnQueue(Q, T);    //根结点入队
    while(!IsEmpty(Q)) {
        DeQueue(Q, p);    //出队队首元素
        visit(p);    //访问p
        if (p->lchild) EnQueue(Q, p->lchild);    //左子树入队
        if (p->rchild) EnQueue(Q, p->rchild);    //右子树入队
    }
}

2.3.哈夫曼树

408数据结构学习笔记——树与二叉树的应用——哈夫曼树和哈夫曼编码、并查集_江南江南江南丶的博客-CSDN博客

1.哈夫曼树的定义：在n个带权叶节点的二叉树中，带权路径长度（从该结点到根节点所经过的边数和该点的权值的乘积）总和最短的树

2.哈夫曼树的构造：每次选择当前权值最低的两个结点合并成一个新的结点（该新结点的权值为被合并的两个结点之和），如此循环直到只剩下一个结点

3.哈夫曼树前缀编码翻译：哈夫曼树的编码可以理解为从根至该字符的路径上边标记的序列，其中变标记为0表示转向左孩子，标记为1表示转向右孩子（也可以0对应右，1对应左）

2.4.并查集

408数据结构学习笔记——树与二叉树的应用——哈夫曼树和哈夫曼编码、并查集_江南江南江南丶的博客-CSDN博客

1.并查集的数据结构定义：采用双亲表示法，数组元素的值即它的双亲结点的数组下标

#define MAXSIZE 100
int UFSets[MAXSIZE];    

2.初始化：将每个结点的值设置为-1，表示每个结点都是一颗单独的树，即n个子集

void InitUFSets(int arr[]) {
    for (int i = 0; i < MAXSIZE; i++) arr[i] = -1;
}

2.Find操作：找到该结点的根节点；根节点的值为负数（-1或者绝对值代表这个树的总结点数）

int Find(int arr[], int x) {
    while (arr[x] >= 0) x = arr[x];    
    return x;
}

3.Union操作：①两个结点都是根节点，直接Union

void Union(int arr[], int root1, int root2) {
    S[root2] = root1;
}

②两个结点是非根节点：先用find找到各自的根节点，再将Union这两个根节点

int Find(int arr[], int x){    //找到x的根节点
    while(arr[x] >= 0) x = arr[x];
    return x;
}
void Union(int arr[], int x, int y){
    int root1 = Find(arr, x);
    int root2 = Find(arr, y);
    arr[root2] = root1;    //将root2的双亲结点改为root1
}

4.Union操作的优化：根节点的绝对值代表这个树的总结点个数，小树合并到大树O（log n） 

void Union(int arr[], int root1, int root2){
    if (arr[root1] < arr[root2]) { //root1为大树，root2为小树
        arr[root1] += arr[root2];    //两个树的结点相加
        arr[root2] = root1;    //root2的双亲结点修改为root1
    }
    else {    //root2为大树，root1为小树
        arr[root2] += arr[root1];
        arr[root1] = root2;
    }
}

5.Find操作的优化（压缩路径）：该结点到根节点路径上的每个结点都挂到根节点上

int Find(int arr[], int x) {
    int root = x;
    while (arr[root] >= 0) root = arr[root];    //跟普通find操作一样，先找到根节点
    while (arr[x] >= 0) {    //逐一修改路径上每个结点的双亲结点为根节点
        int temp = x;
        x = arr[x];
        arr[temp] = root;
    }
    return root;
}

2.5.二叉查找树

408数据结构学习笔记——二叉排序树、二叉平衡树、红黑树_江南江南江南丶的博客-CSDN博客_二叉排序树和红黑树

1.数据结构定义：和普通二叉树的定义一样，只是按左小右大的顺序排列

typedef struct BSTNode{
    struct BSTNode *lchild, *rchild;
    int value;
}BSTNode, *BSTree;

2.查找操作：非递归实现更简单

BSTNode* Search(BSTree T,int key){
    while (T && key != T->data) {    //T当前非空或者当前结点的值不等于key
        if (key > T->data) T = T->lchild;    //key大于当前结点的值，去左子树
        else T = T->rchild;    //key小于当前结点的值，去右子树
    }
    return T;    //返回T所指向的结点，可能是NULL
}

3.插入：根据左小右大的原则，逐层找到空结点插入

4.删除：三种情况

①删除叶子结点：直接删除

②删除只有左子树或只有右子树的结点：让其子树的根节点（即被删除结点的左右子树）代替

③删除有左右子树的结点：根据中序遍历的特性，替换成直接前驱或直接后继

planA：替换成直接后继。找到其右子树的最左下的结点替换（最左下即该结点一定没有左孩子），而被替换的结点由它的右子树的根节点代替（转换成2）

planB：替换成直接前驱。找到其左子树的最右下的结点替换（最右下即该结点一定没有右孩子），而被替换的结点由它的左子树的根节点代替（转换成2）

排序二叉树删除叶子结点后重新加入：不会改变树形结构

排序二叉树删除分支结点后重新加入：一定改变树形结构

2.6.平衡二叉树

408数据结构学习笔记——二叉排序树、二叉平衡树、红黑树_江南江南江南丶的博客-CSDN博客_二叉排序树和红黑树

1.数据结构定义：与二叉树相比多一个变量平衡因子

typedef struct AVLTNode{
    int value;
    int banlance;    //平衡因子
    struct AVLTNode *lchild, *rchild;
}AVLTNode, *AVLTree;

2.查找操作：和二叉查找树一致（平衡二叉树是对二叉排序树的优化）

AVLTNode* Search(AVLTree T, int key) {
    while (T && T->data != key) {
        if (key > T->data) T = T->lchild;
        else T =T->rchild;
    }
}

3.插入操作：

①从添加结点往上找，找到最小不平衡子树

②先将LR型→LL型/RL型→RR型

③LL型：右转，中为根

④RR型：左转，中为根

https://www.bilibili.com/video/BV1xE411h7dd?spm_id_from=333.337.search-card.all.click&vd_source=8089af3b1567624b2594e5459a05e17a

3.图

3.1.最小生成树（Prim和Kruskal）

408数据结构学习笔记——图的应用_江南江南江南丶的博客-CSDN博客_408数据结构

MST不唯一优先使用Kurskal

1.Prim算法：每次选择一个新的未连通的顶点（选点）

①从某一个顶点开始构建最小生成树，依次加入当前剩余顶点中代价最小的顶点，直到加入所有顶点

②时间复杂度：O(||)

③适用：稠密图

2.Kruskal：每次选择未被选取过且权值最低的边（选边）

①每次选择代价最小的一条边，使该边的两个顶点相通，但是，如果原本就相通的两个顶点的边就不选，直到所有顶点相通

②时间复杂度：O()

③适用：稀疏图

3.2.最短路径（Dijkstra和Flyod）

408数据结构学习笔记——图的应用_江南江南江南丶的博客-CSDN博客_408数据结构

1.Dijkstra（单源最短路径）：每次选择一个当前已知最短路径的顶点加入顶点集，然后再经过改顶点更新路径

①选择v1：

②选择v6：

③选择v5：

④选择v2：

⑤选择v4：

 ⑥选择v3：

时间复杂度：O（）

不适用：权值出现负值

2.floyd（多源最短路径）：依次选择图中的顶点加入路径，若经过改顶点到达其他顶点的权值更低，则将该顶点加入到达该点的路径

空间复杂度：创建两个二维数组O(n2)

时间复杂度：三个for循环O(n3)

3.3.有向无环图

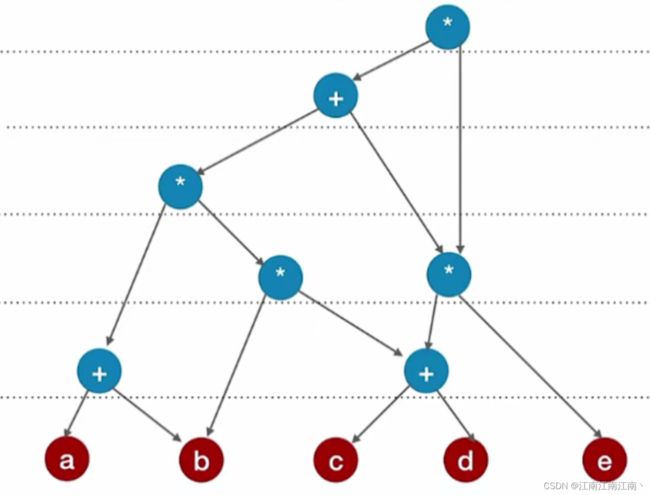
3.3.1.描述算式

 

3.3.2.拓扑排序

1. 从AOV网中选择一个没有前驱的顶点输出
2. 在AOV网中删除该顶点和所有以它为起点的顶点
3. 重复1、2直到AOV网中没有顶点

1→2→4→3→5

3.3.3.关键路径

408数据结构学习笔记——图的应用_江南江南江南丶的博客-CSDN博客_408数据结构

3.4.图的数据结构

1.邻接矩阵（顺序存储）：无向图是实对称矩阵

#define MAXVEX 100    //最大顶点数
typedef struct Graph {
    char vexData[MAXVEX];    //一维数组，存放顶点数据
    int Edge[MAXVEX][MAXVEX];    //二维数组，存放邻接矩阵
    int vexNum, edgeNum;    //顶点数和弧数
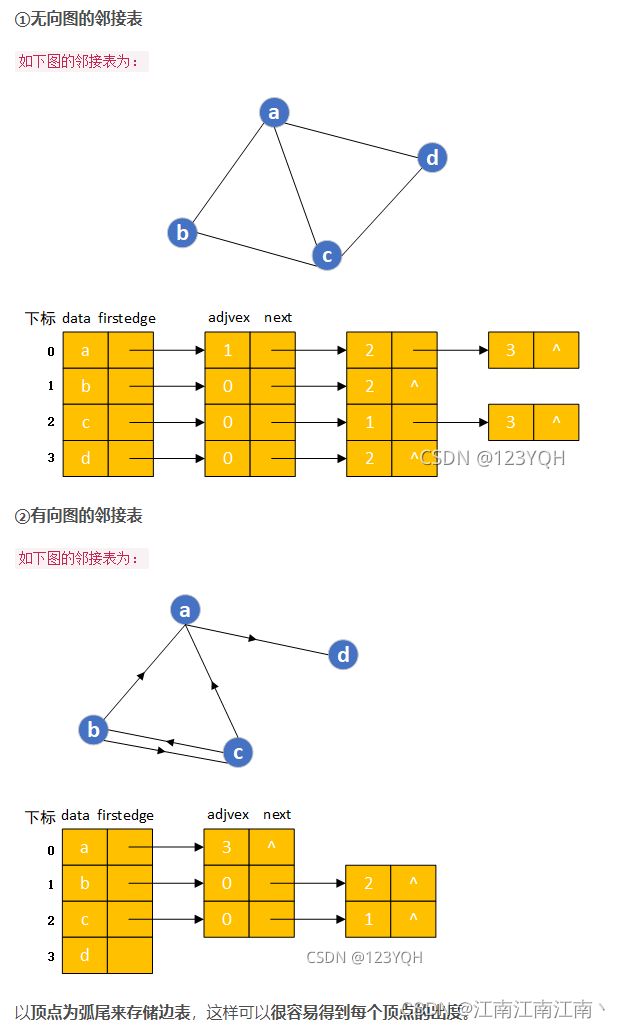
}Graph;

2.邻接表（链式存储）

6.2.2图的存储结构——邻接表法_123_YQH的博客-CSDN博客_邻接表法

#define MAXVEX 100

typedef struct EdgeNode {    //邻接边
    struct EdgeNode *next;    //指向邻接的下一条边
    int adjVex;    //该邻接边对应的数组下标
}EdgeNode;

typedef struct VexNode{    //邻接顶点
    int data;    //该结点的数据
    EdgeNode *firstEdge;    //指向该顶点第一条邻接边
}VexNode, AdjList[MAXVEX];

typedef struct Graph{    //邻接表
    AdjList adjList;    //申明一个VexNode类型长度为MAXVERTEXNUM的一维数组存储顶点
    int vexNum, edgeNum;    //该表的顶点数和弧数
}Graph;

4.查找

4.1.顺序查找

408数据结构学习笔记——顺序查找、折半查找、分块查找_江南江南江南丶的博客-CSDN博客_顺序查找效率

从头到尾逐一对比元素

int Ssq_Search(int arr[], int key, int n){
    int i;
    for (i = 0; i < n && arr[i] != key; i++ ) {
        if (arr[i] == key ) return i;
    }
    return -1;
}

4.2.折半查找

1.算法思想：申明一个mid指针始终指向数组的正中心元素，判断该元素是否为key元素；若是则返回mid（该元素的数组下标）；若不是则判断大小去左右子树查找

该查找方法要求以数组（支持随机访问），并且有序

int Binary_Search(int arr[], int n, int key) {
    int low = 0, high = n - 1, mid;    //初始化low和high指针
    while (low <= high) {    //当low > high 时结束循环
        mid = (low + high) / 2; //每轮循环将mid重置
        if (arr[mid] == key) return mid;    //mid和key相等，返回mid数组下标
        else if (arr[mid] < key) low = mid + 1;    //key比mid更大，则去右边
        else high = mid - 1;    //key比左子树更小，则去左边
    }
    return -1;    //循环内没有return则说明数组中没有该元素，返回-1
}

2.ASL：需要注意一点，查找失败的情况下仅需找到存在的最底层叶子结点，不需要找到空结点

3.时间空间复杂度（顺序查找和折半查找的时间复杂度对比）

4.3.分块查找

1.手算模拟过程

2.ASL

4.4.二叉搜索树和二叉排序树

408数据结构学习笔记——二叉排序树、二叉平衡树、红黑树_江南江南江南丶的博客-CSDN博客_二叉排序树和红黑树

1.算法思想：和折半查找类似

2.代码实现：

BiTNode* Search(BiTree T, int key) {
    BiTNode *p = T;
    while (p && p->value != key) {
        if (p->value > key) p = p->lchild;
        else p = p->rchild;
    }
    return p;
}

3.ASL

4.时间复杂度：计算方式与折半查找相同，特别注意查找失败情况下

4.5.散列表

408数据结构学习笔记——B树、B+树、散列表_江南江南江南丶的博客-CSDN博客

1.处理冲突的方法

①线性探测：注意散列因子求散列表长的方式计算散列表查找成功和查找不成功的平均查找长度（利用线性探测法处理冲突）_叫我蘑菇先生的博客-CSDN博客_线性探测法查找失败的平均查找长度

②拉链

2.ASL

①线性探测：注意查找失败时，只需计算散列函数的初始可能取值的个数，即mod 7 只计算开始的 0 - 6号散列表元素各自到第一个空元素的和（并非整个散列表）

②拉链：注意查找失败时，空指针不算一次查找次数

4.6.kmp算法

408数据结构学习笔记——串、朴素模式匹配、kmp算法及其改进_江南江南江南丶的博客-CSDN博客

1.next数组

2.next[j]的定义（next[1] = 0，next[2] = 1）

3.nextval（next[next[j]]）

5.排序

1.记忆口诀：

马士兵说：30秒让你记住所有排序算法-宋词记忆法_哔哩哔哩_bilibili

选泡插，快归堆希统计基：选择，冒泡，插入；快速，归并，堆，希尔，桶，计数，基数

恩方恩老恩一三，对恩加K恩乘K：选择，冒泡，插入为O（n2）；快速，归并，堆为O（nlogn）；希尔为O（n1.3）；桶和计数（不要求）为一对的O（n+K）；基数为O（n * K）

不稳稳稳不稳稳，不稳不稳稳稳稳：分别按上面对应

2.

408数据结构学习笔记——直接插入排序、折半排序、希尔排序_江南江南江南丶的博客-CSDN博客

408数据结构学习笔记——简单选择排序、堆排序_江南江南江南丶的博客-CSDN博客

408数据结构学习笔记——冒泡排序、快速排序_江南江南江南丶的博客-CSDN博客

408数据结构学习笔记——归并排序、基数排序_江南江南江南丶的博客-CSDN博客

408数据结构学习笔记——外部排序_江南江南江南丶的博客-CSDN博客

3.对比次数、稳定性、时间/空间复杂度、手绘过程（希尔、堆、基数）