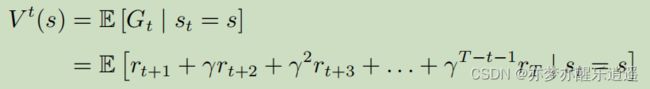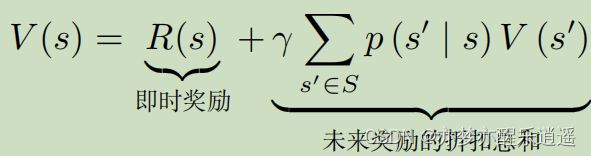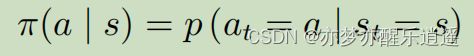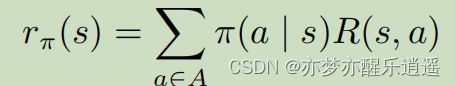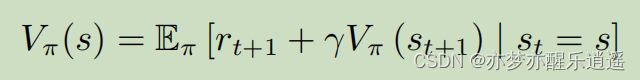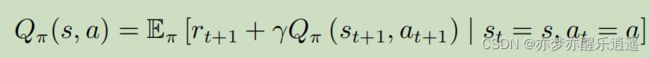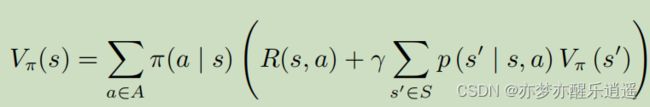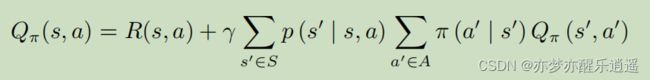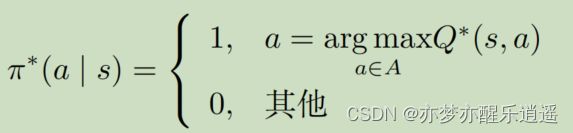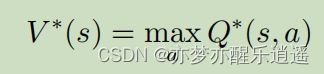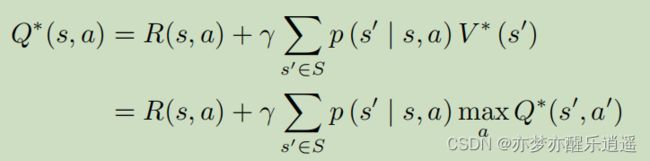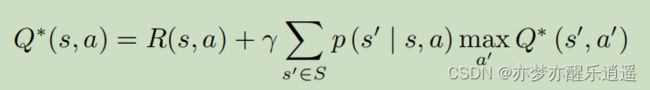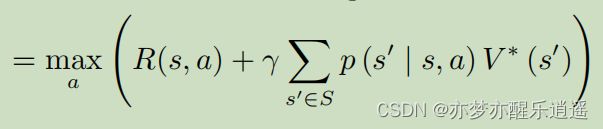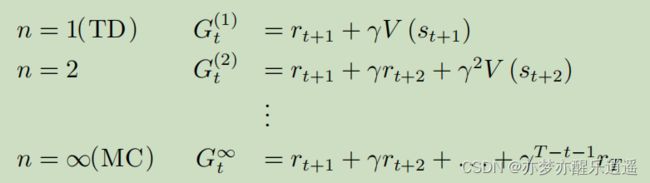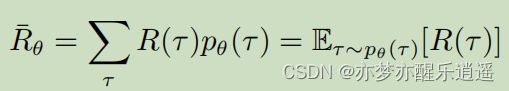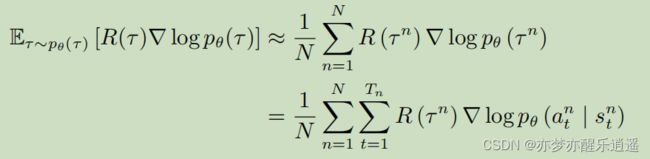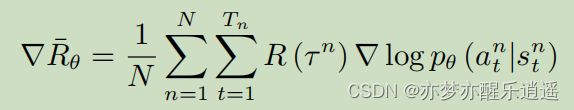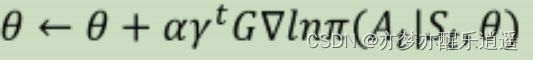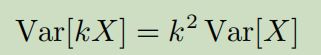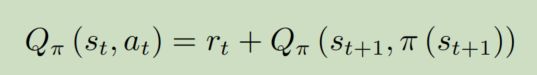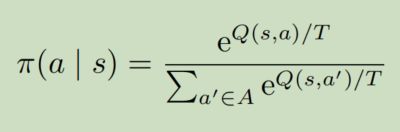《EasyRL》强化学习笔记
文章目录
- 概览
-
- 基本概念
- 系统构成
-
- Agent与环境
- 策略
- 奖赏函数
- 值函数
- 环境模型
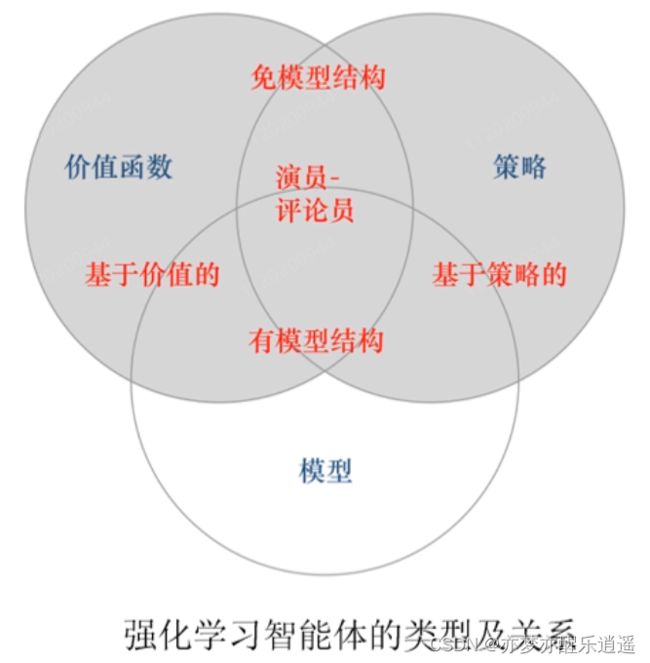
- 强化学习分类
- 强化学习与监督学习|非监督学习的区别
- 例子:playing pong
- 新技术:深度强化学习
- 马尔科夫决策过程
-
- 马尔科夫过程(MP,Markov Process)
-
- 马尔科夫性质
- 马尔科夫链
- 马尔科夫过程的例子
- 马尔科夫奖励过程(MRP)
-
- 回报(G)与价值函数(V)
- 贝尔曼方程
- 计算马尔科夫奖励过程的迭代算法
- 马尔科夫决策过程(MDP)
-
- 相比于MRP的变化
-
- MDP中的策略(Policy)
- MDP和MRP的关系
- Q函数与V函数
- 贝尔曼期望方程
-
- 备份图
- 策略与控制
-
- 策略评估
- 控制
- 动态规划
- MDP控制方法
-
- 策略迭代
-
- 策略迭代方法
- 贝尔曼最优方程与Q学习
- 价值迭代
-
- 最优性原理
- 确认性价值迭代
- 价值迭代算法
- 策略迭代和价值迭代的区别
- 关键概念
- 表格型方法
-
- 马尔科夫决策过程
-
- 有模型
- 免模型
- 有模型和免模型的区别
- Q表格
- 免模型预测
-
- 蒙特卡洛策略评估
- 时序差分
- 动态规划方法、蒙特卡洛方法以及时序差分方法的自举和采样
- 免模型控制
-
- Sarsa:同策略时序差分控制
- Q-learning:异策略时序差分控制
- 关键概念
- 策略梯度
-
- 策略梯度算法理论
- 策略梯度实现技巧
-
- 添加基线
- 分配合适的分数
- REINFORCE:蒙特卡洛策略梯度算法实例
- 关键概念
- 近端优化算法(PPO)
- 深度Q网络(DQN)
-
- 强化学习的本质
- 网络近似
-
- 状态价值函数
- 动作价值函数
- 必备技巧
-
- 目标网络
- 探索
- 经验回放
- DQN整体思路
- 关键概念
- DQN衍生技巧(Tricks of DQN)
-
- Double DQN(DDQN)
- 深度竞争Q网络(dueling DQN)
- 优先级经验回放(PER,prioritized experience replay)
- 多步方法
- 噪声网络(noisy net)
- 分布式Q函数(distributed Q-function)
- 彩虹(RainBow is All You Need)
概览
本文脱胎于蘑菇书:Eazy-RL
这本书感觉写的还是相对顺畅的,耐心把公式看下去,基本没有理解障碍。
我没有全部看完,仅仅是看完了DQN,策略梯度没有研究,后面如果有时间会学一下
基本概念
机器学习是比较宽泛的概念,其中既有诸如聚类之类的传统机器学习方法,也有如深度学习,强化学习之类的子领域。
这两个子领域因为效果比较好,已经和父领域有平起平坐的感觉了,人们平时说起深度学习或者强化学习,是不会把他们归到机器学习里的。
所以,强化学习虽然基于机器学习,但是和机器学习的依赖关系并不明显。
在机器学习的分类中,有监督学习,非监督学习,以及强化学习。
所以强化学习可以说是一个比较重要的领域了。
其实强化学习就是我最开始对人工智能的理解,我没学人工智能之前,我就觉得,学习的过程就是不断试错,积累经验。强化学习也是如此,强化学习主要是两部分,一个是智能体,另一个是环境,智能体在和环境交互的过程中成长。智能体就是Agent,Agent做出动作Action,对环境做出影响,同时环境给出反馈,给Agent一个奖赏值(也可能是惩罚),同时改变Agent的一些状态。
具体举个例子,就是训练鹦鹉。鹦鹉如果说脏话(Action),就会受到惩罚,打一下脑袋,这个时候鹦鹉本身已经被改变,它下一次说脏话的可能性就很小了,如果他说你好之类的话,就会收到吃的,它下一次就会更倾向于说好话。这就是一个典型的强化学习,所谓强化,就是通过一次又一次的反馈,强化某些特征,弱化某些特征,把Agent塑造成你想要的模样。
不过这种模式也有缺点,就是学习效率比较低,需要积累经验,这是一种纯粹的实践性学习,高级的学习方法应该是理论+实践的结合,但是也可以改进,AlphaGo不就是一个成功案例吗。

系统构成
Agent与环境
策略
策略的输入是状态与环境,输出是Action。
确定性策略比较直接,随机策略引入概率,随机性,如果学过最优化,就会明白奖赏的本质是贪心策略,贪心策略容易陷入局部最优,而这种随机性的引入有利于全局最优(参考模拟退火,感觉和这个有点像)。


奖赏函数
奖赏函数输入:状态,动作
输出:奖赏
值函数
环境模型
环境模型简称为模型,代表了智能体如何理解世界,即世界的编码。

强化学习分类
强化学习与监督学习|非监督学习的区别
这里就可以探讨一下这些任务的区别了。
经典机器学习(包括深度学习在内),都是一种模式识别。所谓模式识别,比方是给你一个图片,你告诉我是什么。那训练的时候就可以拿大量独立同分布的图片去并行地训练。
但是很明显,强化学习就是一个随着时间迭代的过程,是纯粹的串行,他的Action,奖励,反馈,都是一种序列,不可能独立同分布。
另一个角度来说,他的反馈是延迟的,比如打砖块游戏,反弹以后等一会才会有反馈。
至于说没有监督者,严格来说确实是没有的,但我觉得奖励信号本质上就起到监督作用,督促着系统向着目标状态迭代。
这里给出区别
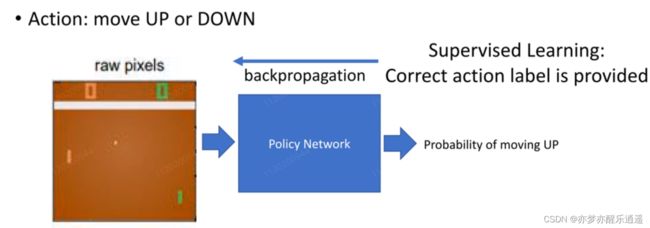
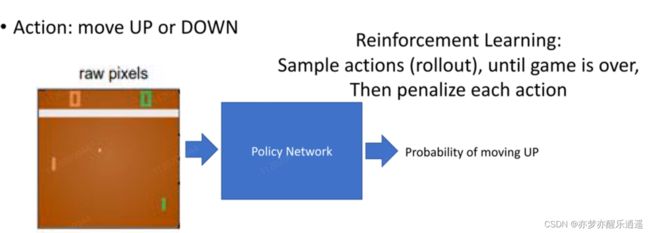
例子:playing pong
首先,将图片(环境+状态)作为输入,送到神经网络中,进行决策,最后通过sigmoid函数给出移动的概率。

下面的图片是通过监督学习的方法进行训练。用上下作为标签,进行训练。但是这样的训练很明显没有时序信息。
下面的图片是通过强化学习的方式训练,神经网络仅仅负责决策,训练的过程是按照前面的那个流程图训练的。
不断试错,失败就重新来过,直到积累的经验发生质变,使得决策模块生成的指令序列可以让游戏一步一步走向胜利。
新技术:深度强化学习
深度学习对于特征的提取和拟合能力比较强,所以决策模块完全可以用神经网络来负责,直接实现端到端训练。而传统的决策模块可能分成很多步骤,逐步提取特征,比如HOG+DPM+SVM。
马尔科夫决策过程
强化学习基本框架符合马尔科夫决策过程。
马尔科夫过程(MP,Markov Process)
马尔科夫性质
未来状态仅与当前状态有关,就叫马尔科夫性质。
本质来说,未来状态实际和过去所有状态有关,毕竟,没有过去,哪来现在?但是从公式来说,确实是只需要知道现在就可以决定将来,从表面上说,马尔科夫是无记忆的。
如何描述马尔科夫过程?
马尔科夫链
如果状态是离散的,那么就叫马尔科夫链,这个概念在数学建模中也经常出现。
状态矩阵的特点在于,只要起始状态在矩阵中,那么生成的结果状态一定可以作为另一个转换的起始状态。即,无论怎么转,都不会脱离状态空间。
又因为状态是离散的,所以可以用节点表示状态,用转移线表示转移概率,就会有这种类似于状态图的图:
马尔科夫过程的例子
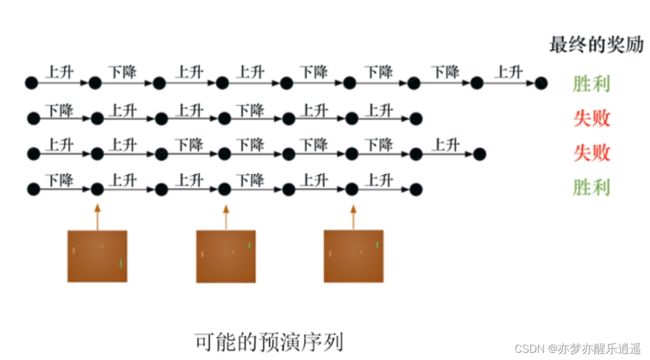
从s3开始进行采样。
之所以要采样,是因为状态转移是概率性问题,从s3走5步,可以走到s6,但是重来一次或许就是s1。
在强化学习中,这么走一轮叫 回合。
马尔科夫奖励过程(MRP)
MRP增加了一个指标:Reward(简写为R)
奖励函数 R 是一个期望,表示当我们 到达 某一个状态的时候,可以获得多大的奖励。
形式上,一个状态对应一个r值,如果状态有限,R可以表示为一个向量。
还有一个伴随而来的量,价值函数V,表示我们 在 某一个状态的时候,未来可能获得多大的奖励,如果V大,说明从当前状态出发就可以获得更多的奖励,状态就更有价值。
回报(G)与价值函数(V)
前面说到回合,回合的长度叫Horizon,表示一个回合要走Horizon步。
首先给出回报函数。
从t时刻开始的一个回合的回报函数表示如下,注意,回报函数是针对一个回合的,该回合从t时刻开始:
- 可以看出,回报函数指从当前状态出发走一个回合获得的实际好处。
- 分析一下G函数,首先,G函数中要用到r,所以我们姑且不去管R是如何来的,先用。可以看到,随着步数的增加,奖励系数是越来越小的( γ \gamma γ 一般是小于1的),所以越近的步对于回报函数的影响越大。
- 之所以要用折扣因子,有如下原因:
- 让奖励收敛,防止无穷无尽的奖励。
- 因为我们对环境并不一定全知,所以相信最近的几步可以保证策略的稳定
- 折扣因子可以用于调参 - 之后探讨一下t,t是参数吗?不是。因为马尔科夫过程是时间稳定的,即P不会随着t改变。之所以用t,是便于描述一个回合,虽然你从什么时候开始无所谓,但是你一个回合走得时间就是那么多(T)
基于回报函数,得出状态价值函数为回报函数G的期望:
- 为什么是期望呢?因为以s作为开始状态的采样序列可以有多种,每次采样都可以得到一个实际回报 G t G_t Gt,通过多次蒙特卡洛模拟,可以算出G近似的期望,即 V t ( s ) V^t(s) Vt(s)
- 为什么要叫状态价值函数?实际上这个函数更多的是对于后续步骤的收益期望,一个状态在未来可以获取的收益就代表了这个状态本身的价值。从这个意义上说,未来收益=当前状态价值
- 关于参数s。前面说t不是参数,但是这里的s是参数。这里的st=s代表回合的起始状态为s,所以 V t ( s ) V^t(s) Vt(s)是关于s的函数,t的含义仅仅代表序列的起始,这也呼应了稳定的马尔科夫过程与时间,与某一次回合无关的特点。
- 最后一个问题来了,R怎么求?其实R是人给定的,你在指定游戏规则的时候,其实就相当于指定了R,比如赢了就+100,输了就-100。
贝尔曼方程
上面说到计算V,上面的方法是蒙特卡洛方法,是近似解。还有一种办法,是解析解。
首先给出贝尔曼方程,怎么来的别管。
整体来看,当前状态的价值=走到当前状态收获的奖励+转移后可能的价值(转以后可能获得的总奖励)
说白了,当前价值就是可能收获的总奖励,所以贝尔曼方程是很合理的。
很明显,这是一个线性代数,而且是一个迭代方程。但是我们可以通过线性代数变换,得到V向量的解析公式:
这个时候求出逆矩阵就可以求得V,但是求逆矩阵的时间复杂度是 O ( n 3 ) O(n^3) O(n3),如果状态变多,速度会很慢。
计算马尔科夫奖励过程的迭代算法
对于V的计算
前面讲了蒙特卡洛和解析方式。这里给出更多迭代算法,比如动态规划,时序差分(TD,temporal difference learning)
蒙特卡洛具体的伪代码:

动态规划的方法就是迭代法。之前有一个贝尔曼方程,如果我们不变形,那他本身就是一个迭代公式。这种用其他估计值更新某一个估计值的方法,就是一种自举(bootstrapping)迭代。学过数值分析,写过代码的人会对这个过程非常熟悉,就是判断,迭代,更新,直到更新的和前一次差不多为止:
马尔科夫决策过程(MDP)
相比于MRP的变化
到这一步,马尔科夫过程终于和RL联系了起来。
在MDP中,决定下一状态的,除了当前状态,还有当前的Action。这也合理,如果没有Action,马尔科夫链在执行过程中概率是会收敛的,是定死的过程,但是加了Action的影响,马尔科夫过程就盘活了一些

增加了一个动作参数,那对于不同的动作,其状态转移矩阵都是不同的,即一个动作对应一个状态转移矩阵。
一般来说,已知状态和行为,下一个状态就基本确定了,所以转移矩阵中的p一般要么是1要么就是0。但是之所以要给个p矩阵,是因为有时候你采取了行动,结果也不一定按照你的意愿来,比如你要往上走,但是环境比较湿滑,你滑到了右边,这就是意料之外的事情,环境的不确定性越强,S和A对P的决定性就越弱。反之,如果S是完全知道可预测的,P矩阵中的转移一般就都是1或者0了。
奖励函数也变了,因为不同的a对应的 R a R_a Ra是不一样的,所以对所有a之下的R进行求期望,就是最终的R。
MDP中的策略(Policy)
根据当前状态采取Action的函数就是策略函数。
策略给出的是所有Action的概率分布,并非准确的某个结果。当然,策略也可以输出结果。
MDP和MRP的关系
如果策略函数 π \pi π是给定的,那么MDP过程本质上还是MP,因为Action是被s决定的,s1由s和A决定,那s1实际上还是仅由s决定的。
MDP和MRP的区别仅仅在于,MDP中间夹了一层Action,但是Action还是被s决定的。MDP是可以被替换成MRP过程的。
先看MDP下的转移公式
这个公式可以理解为:从s开始,我可以采取各种Action,但是最终要到s1状态,每一个Action都是一种实现路径,把这些路径的概率加权求和,就是从s到s1的MRP概率。
奖励函数公式也可以替换的
在s状态下可以采取不同Action,每一种Action都有一种奖励,把这些奖励求个期望,就是s状态下的奖励。
Q函数与V函数
之所以有 π \pi π作为下标,是因为这一切的前提是策略已经给定。

这个V和MRP中的V是一样的,为什么呢?因为MDP可以变成MRP,推导在下面。
为了更好的描述MDP下的状态价值函数,这里先引入动作价值函数Q-function
Q函数代表在一个状态下,采取一个动作后的V函数。
Q函数和V函数的区别仅仅在于Q函数是确定Action后的V函数。
很合理的,对Q函数概率加权就可以得到V函数。
一个状态下,有 π \pi π概率采取某个行动,这些行动的加权就是这个状态下进行下一步行动(行动未知)的期望收益。
这里可以看出,虽然有Action作为中间变量,但是MDP中的V和MRP中的V实质上没有区别。
贝尔曼期望方程
继续将MDP转化成MRP,用Action做加权分解,这次拿贝尔曼期望方程开刀。
V和Q,两个函数,在MRP情况都是有贝尔曼形式的。
这里用Action分解,V和Q就变成了期望形式,权值为Action概率。
上面两个式子比较抽象,进一步代入符号解释:
首先给出两个辅助公式:
这是MDP下V的公式(含Q)

这是MDP下Q的贝尔曼函数(含V)

这两者都是双变量公式,并不好,但是你中有我我中有你,自然可以相互消,变成单变量的迭代形式。
分别用1式带2,和2式带1,消去变量可以得出两个公式,这两个公式是真正意义上的的V和Q在MDP下的贝尔曼形式。
这个是V值的迭代形式(MDP下的贝尔曼形式)

这个是Q的迭代形式(MDP下的贝尔曼形式)

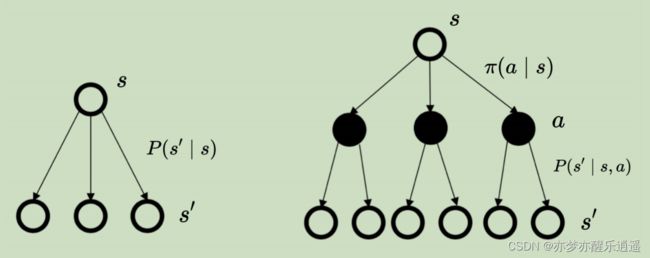
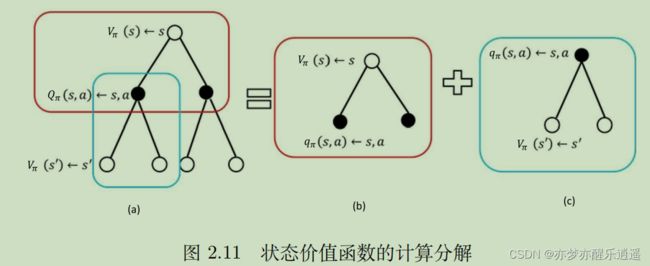
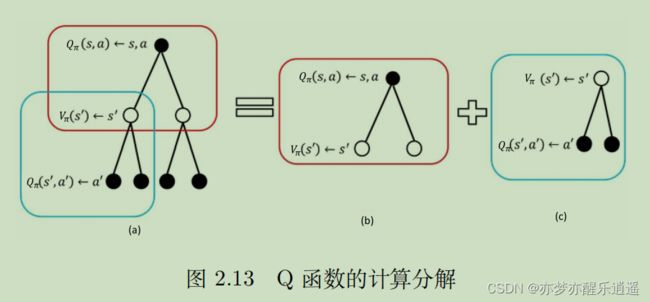
备份图
以上两个公式,既可以看成是从当前(V)推未来( V ′ V^\prime V′),也可以看做从未来推当前。备份图和贝尔曼公式本质上是一样的,只不过备份图是一种图形化表示,而且如果可以把中间结果储存起来,可以起到动态规划+备份的效果。
首先是状态价值函数的计算。
可以看到,这就是前面给出的MDP下关于V的贝尔曼公式,两层图像代表先用 V ′ V^\prime V′算Q,再用Q算V。
先进行最底层层累加,对应于下图中(c)的计算,然后进行中层累加,就是(b)的计算。这两个结合起来就是V的回溯。
策略与控制
策略评估
到此为止,一个MDP回合也可以顺着走下来了,并且还可以通过备份回溯。
一个MDP过程可以用
给定一个初始状态,Agent会根据策略采取行动,采取行动后由P矩阵进行状态转移,进入下一轮决策。在不断的状态转移中,到达目标状态。
从这里可以看出,状态集S和行为集A给定的前提下,强化学习的核心就在于策略。
如何评价一个策略的好坏呢?用价值函数 V π V_\pi Vπ,好的策略可以让每一个状态的价值都提升到最大,只要按着策略走,就一定能获取很高的收益,这也是V的含义。
书上给了两个例子,我就不赘述了,但是总的来说,其实就是给定
控制
预测就是给定
而控制,就是给定
当然,具体的方法肯定没那么粗暴,但是当找出最佳的 π \pi π的时候,一个强化学习模型就可以说构建好了。
动态规划
TODO
这一块不是太理解,后面再补
MDP控制方法
所谓的最佳策略函数,就是让每个状态的价值都达到最大。策略搜索肯定不能用枚举,一般用策略迭代和价值迭代。
如果能令V最大,那么就说明这个MDP可解,虽说V的上限固定了,但是最佳策略却可以有多种,他们都有相同的V。
在这种情况下,优中选优,就可以挑选策略稳定性最强的策略了。具体来说,就是使Q函数最大化来得到最佳策略,直观来说,就是在给定s后,只会采取一种行动,其他行动的概率都是0,每个状态对应一种确定的Action。
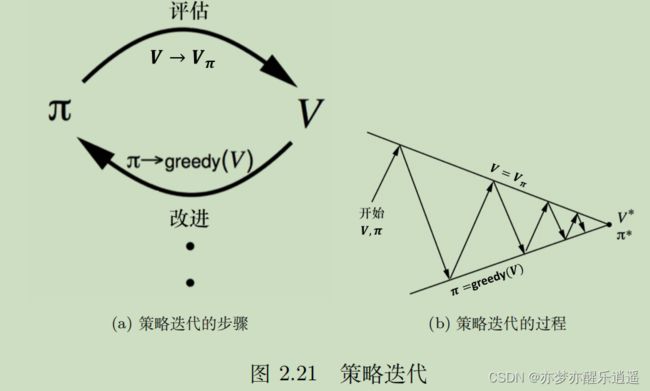
策略迭代
策略迭代方法
策略迭代是策略改进的一种方式。
在策略迭代中,先对策略进行评估,算出当前策略对应的V,然后基于V和a就可以计算Q函数,通过Q函数的最大化来产生新策略。这是一个轮回,在不断地迭代中,V不断增大,最终V的变化会逐渐收敛(理论不明,反正肯定能收敛)
具体说一下如何进行策略改进,即Q函数如何最大化:
Q函数是给定了a的前提下,对一个状态+行为的价值评估。即Q是s和a的函数。
对于某个状态,s已经固定,给不同的a就会算出不同的Q,这些Q里面会有一个最大的Q,其对应一个参数a,之后就以这个a作为确定策略。

为了更好地执行这个过程,采用表格进行图形化操作:
横轴是状态,纵轴是可能的动作,选择新策略的过程就是从左往右遍历每一列,从每一列中取出最大的Q对应的格子。
这里有一个疑问,你把策略弄成固定的,不会影响下一次策略迭代吗,下一次还能选择其他策略吗?
其实这两个没啥关系,你改了策略,计算的V就变了,V变了,选出来的最大的Q很有可能就变了,比如你原来的策略是up(Q最大),但是你后面发现采用新的策略后还可以有更好的策略down(Q也是最大)。虽然pi对每一种s是固定的,但是旧策略选某一个a不代表新策略就不能选别的,所以还是可以计算出一系列a对应的Q的,第i次pi只能决定V,不能决定在这种V下的a。
贝尔曼最优方程与Q学习
因为每次改进策略后,action都固定了,所以固定a对应的那个Q(a,s)函数其实就和V(s)相等。
即,每次改进策略后,都可以把Q和V互换,这就是贝尔曼最优方程。
V迭代到最优后,再次进行Q最大化,就可以达到下面的对应关系。
在满足上述贝尔曼最优方程的前提下,对Q函数(含V)的贝尔曼形式进行变形,就可以得到如下形式:
这代表了在当前最优情况下,Q函数的迭代关系,Q-learning就是基于这个公式进行学习的
当然,也可以把Q代入V中,就可以得到 V ∗ V^* V∗的迭代公式:
价值迭代
最优性原理
难以解释,我也不太明白
确认性价值迭代
这个公式就是我们前面推出的 V ∗ V^* V∗迭代公式。其实V不一定要全局最优,只需要是当前最优,就可以不断地迭代下去,令V逐渐增大,变成 V ∗ V^* V∗
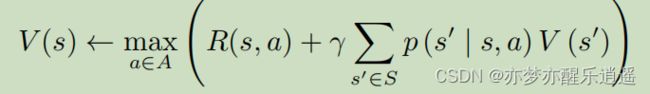
迭代多次之后,价值函数就会收敛。这种价值迭代算法也被称为确认性价值迭代(deterministic value iteration)。
价值迭代算法
三步走:
策略迭代和价值迭代的区别
策略迭代,本质上使用的是贝尔曼期望方程:
- 先对策略进行评估,计算V
- 用V算Q,最大化Q来改进策略
- 1,2步循环迭代直到V收敛,此时再改进后的策略就是最佳
价值迭代,本质上使用的是贝尔曼最优方程:
- 不断迭代V
- 最后从 V ∗ V^* V∗中提取最佳策略
关键概念
马尔科夫性质(Markov Property):一个状态的下一个状态形式上只取决于当前的状态,与之前的状态都没有关系。进一步讲,满足马尔科夫性质的全过程,实际上只由最初状态决定。
马尔科夫链(Karkov Chain):离散状态下的马尔科夫随机过程。
状态转移矩阵P:给定State和Action(可选),进行状态转移的概率矩阵。本质上是一种条件概率。
马尔科夫奖励过程(MRP):给马尔科夫链加上一个奖励函数,给过程附加奖励属性
马尔科夫决策过程(MDP):增加一个Action属性,给过程以方向。
蒙特卡洛算法:用模拟的方法去估算价值函数
动态规划算法:基于贝尔曼期望方程,直接用迭代的方法逼近价值函数
Q函数:给定S-A,预计得到的总回报期望
MDP评估(预测):给定MDP决策过程(S,A,R,P, γ \gamma γ) 和 π \pi π,计算V值与Q值。在PR已知的情况下,可以直接使用动态规划方法(而不是蒙特卡洛)。
MDP控制:给定(S,A,R,P, γ \gamma γ),找出最佳的策略,使得V值最大。已知PR的情况下,同样可以通过动态规划方法解决。分为策略迭代和价值迭代。
表格型方法
表格型方法指的是策略用表格来表示。
经典的表格型方法有蒙特卡洛,Q-learning,Sarsa。
马尔科夫决策过程
强化学习本质上是一个序列决策过程。这个过程具有马尔科夫性质,所以是一种马尔科夫决策过程(MDP),MDP也就是强化学习的基本框架。
强化学习过程一般用元组给出:(S,A,P,R, γ \gamma γ)
有模型
在MDP中,使用P和R对环境进行描述。P代表了智能体在一定状态下采取行为后发生的改变,概率代表了这种改变有随机性,而这种改变必然被环境决定。R代表智能体采取行为后从环境得到的奖惩。虽然不是直接描述环境,但是已经把环境描述出来了。
如果P和R已知,那就可以说环境是已知的,在一切都已知的前提下,可以说是全知全能,运筹帷幄,可以算出最佳策略,一步一步按照最佳策略走,即使是碰到了转移概率中的意外情况,也可以在新的意外状态下继续按照备用的最优计划前进。这就是动态规划。
免模型
然而,生活中更常见的情景是身在局中不知全貌,PR没有那么清楚。人类是在不断地尝试中(尝试Action,探索各种路径),才获得了P和R的信息的。
有模型和免模型的区别
有两种情况无法使用有模型方法:
- 环境未知
- 环境太大,即使是用了迭代方法计算量仍然太大。比如雅达利游戏,围棋,控制直升飞机,股票交易等,状态转移过于复杂。
有模型方法不用和环境交互,直接确定最佳策略。免模型方法不使用P和R,而是让智能体和环境交互,采集大量的轨迹数据,改进策略。这也就是我们最常见的学习思路。

P,R的未知性导致了动态规划方法无法使用,只能使用蒙特卡洛衍生的方法。所以不需要每次策略改进就进行大量迭代,只需要走一回合/一步然后对部分Q表格进行增量式更新,然后基于Q表格做策略改进即可。
个人感觉这样走精度略微下降一些,但是效率比每次更新都要迭代无数次的动态规划方法要高出不少
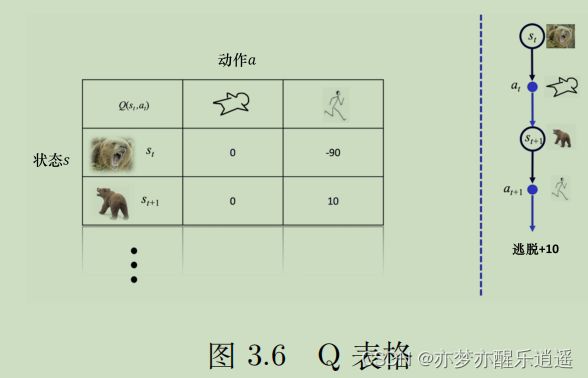
Q表格
免模型的方法通过大量的轨迹去归纳给定s和a情况下的价值Q,将Q函数储存在一张表中,就是Q-Table
Q-Table的行代表一个状态,列代表行为,每一个格子就是一个Q函数值。
如何构建Q表格呢?或者说,如何通过大量的轨迹去归纳Q函数值呢?
以悬崖行走问题举例:
给定一条轨迹,就意味着给定一系列元组,每个元组都是(s,a),对应Q表格中的一个方格。以下图举例,s就是横纵坐标二元组,a就是上下左右。红线告诉你,在这条路径中,s=(1,0),a=右的Q值为-12,s=(1,1),a=右的Q值为-11,s=(1,11),a=下的Q值为-1。这些可以直接加入Q表格。
Q函数的定义是,给定s和a,后续各种路径获得的总收益的平均值,所以以上的一个轨迹的Q值和真实Q肯定是相去甚远,但是在不断增加轨迹的过程中,Q值会不断更新,直到变得合理。
下图给出了给定路径下Q值的计算,可见Q的计算是倒着算的,从路径末尾算到路径出发。
强化的概念就是用下一个状态的价值来更新当前状态的价值(不太理解)
这里重提一下折扣因子的意义。
折扣因子为0的时候,学习是短视的,一般不这么干。但是折扣因子为1,又太过注重未来了,而忽视了眼前唾手可得的利益,所以采取0-1之间的恰当的值。
免模型预测
注意,包括上面讲的Q表格,都没有涉及到 π \pi π以及其调整,也就是说现在只是单纯的讨论预测与评估,没有涉及到控制。
蒙特卡洛策略评估
蒙特卡洛方法的核心是大量采样后求均值。
简单说一下思路,该方法每个回合更新一次。走一个回合,就可以从终点倒推算出路径上每个状态(伴随一个a)的临时Q值,然后和以前的Q值进行一个平均就行。平均是靠记录N(s)来实现的,每次访问一个Q格子就给N加一,然后通过累积的Q值求平均即可。这种叫经验均值(empirical mean return)
在下图中,忽略了a这个参数。那么要更新的Q表格实际上就缩成1维的了,因为没有a了,求出来的也就是状态价值函数了。但是我个人认为,完全是可以考虑到a的,每一个Q方格都用一个N和S来累积,也完全可以应用蒙特卡洛方法,一次更新一条路径上的Q方格。
考虑到保存S的累加可能面临溢出的问题,以及一些出于效率的考量,求均值可以用增量均值的方法(上面是经验均值)
蒙特卡洛相比于动态规划来说,不需要自举那肯定是不用说的,因为你没有P和R,想进行自举迭代都不行。蒙特卡洛方法真正的优势在于,一次迭代只需要更新一条路径的Q方格,而不是所有Q方格。而蒙特卡洛的缺陷是只能在有限长度序列中学习(因为要跑回合)
在贝尔曼期望方程中,要对状态和动作进行两层求和,且一次更新所有状态,能耗比较大。
而蒙特卡洛方法中,一个回合覆盖的状态-行为对也就那么一串,更新的代价很小。
然而,我不认为蒙特卡洛效率就高到哪去了,因为人家虽然一次更新消耗大,但是人家一次更新的也多啊。所以效率之争有待商榷,但是不可否认的是,蒙特卡洛更新的粒度比较小。
时序差分
时序差分可以看做是介于蒙特卡洛与动态规划自举之间的方法。
这里重新审视一下自举,为什么可以通过下一步的V估算这一步的V。比如你平时要上课,路上如果顺利,10分钟就到了,但是某一天你堵车了,堵了5分钟,你就可以通过平时的经验推算出来,这次估计要花15分钟了,即使你还没有走下面的路。
蒙特卡洛算法就相当于,每次都是走完了,通过事实改善自己的认识。但是实际上,不需要完全走完就可以更新V了,甚至你只走一步就行了,这就是一步时序差分(one-step TD),即TD(1),具体公式如下:
上面的公式看着很眼熟,你再仔细回忆一下蒙特卡洛的增量形式,就会发现TD target(时序差分目标)就是G的估计值。这个估计值=走了一步以后的实际收获+这一步以后可能的折扣收获总和。(其实这个公式里没有对A的考虑,是比较粗略地估计V,后面的Sarsa给出了估计Q的方法)
这就是我们前面说的,不需要完全走完就可以利用已有的旧估计值去计算新的估计值。虽然刚开始这个 V ( s t + 1 ) V(s_{t+1}) V(st+1)不靠谱,但是随着迭代次数增加,会逐渐靠谱起来,实际上,随着你对事情了解的加深,你的经验也就越来越稳定了。
既然有TD(1),那也自然有TD(2),TD(n)了。实际上,随着你TD参数的不断增加,对G的近似也就越来越趋近于真实走一趟的G,当n代表终点的时候,TD也就退化成了MC(蒙特卡洛)
这里对比一下这两种方法吧:
- 时序差分牺牲了一部分准确性,换来了高频率的更新,每走一步都可以更新一次。蒙特卡洛得走完一趟才能更新一次。
- 时序差分限制了步数,所以可以适应无限步长情况,也可以适应不完整序列的情况。
- 时序差分从本质上来说,是利用了马尔科夫性质,在马尔科夫环境下有更高的效率。但是如果没有马尔科夫环境效果就会比较差(但是什么环境没有马尔科夫性质呢)。而蒙特卡洛完全基于事实,不受P和A的影响,能够适应一切环境(代价就是效率低一些)
动态规划方法、蒙特卡洛方法以及时序差分方法的自举和采样
动态规划和蒙特卡洛是两个极端,动态规划完全不依赖采样,只依赖P和R(已知的环境信息)进行贝尔曼期望迭代;蒙特卡洛不管环境,完全依赖采样时;序差分介于两者之间,一部分是采样,一部分是自举。
从计算的角度来说,动态规划是逐层计算,蒙特卡洛是计算一条,时序差分是前期计算半条,后期局部逐层计算(没有转移矩阵,其实应该没有按权求和)

最后结合穷举法,给出策略评估的四象限图。动态规划更像BFS,蒙特卡洛是DFS,时序差分介于两者之间,穷举搜索完全穷尽。
免模型控制
在策略迭代中,进行Q函数优化时,需要用P和R计算Q函数,但是免模型情况下,没有P和R,所以把策略迭代推广,兼顾蒙特卡洛和时序差分的方法,即广义策略迭代。
广义策略迭代中,将策略评估部分替换成蒙特卡洛/时序差分,得到Q函数的近似,之后再进行策略改进。不过策略评估中,蒙特卡洛还要稍微改一下,因为每次优化策略后,Action就固定了,为了防止局部最优,使用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy搜索,每次采样的时候,会有 ϵ \epsilon ϵ的概率不按照Q函数执行Action,而是随机执行。这保证了在初期对状态空间的充足探索。随着时间增加, ϵ \epsilon ϵ会逐渐减少,最后就完全按照Q函数决定动作了,策略也就逐渐固定了。
理论上可以证明,使用蒙特卡洛方法和 ϵ − g r e e d y \epsilon-greedy ϵ−greedy搜索可以保证V单调递增。下图给出伪代码,这里的Q函数是s和a的二元函数,符合我前面的推测。
除蒙特卡洛,也可以把蒙特卡洛替换成时序差分,同时引入 ϵ − g r e e d y \epsilon-greedy ϵ−greedy搜索。这种方法具有低方差,在线学习,可以从不完整序列中学习的优点。
书中提到了基于探索性开始的蒙特卡洛方法,有点迷惑。TODO
Sarsa:同策略时序差分控制
Sarsa就是用时序差分方法构建Q表格的一个算法。
前面给出的时序差分公式是更新V的,这里变成了更新Q(TD(1))。把V变Q思路和蒙特卡洛一样,只针对路径上的(s,a)二元组更新Q表格中的一部分。
![]()
因为算法每次更新需要用到两Q一R,即知道S(当前状态)A(当前Action)R(下一步奖励)S(下一状态)A(下一Action),这也是算法名字由来。
下图给出基本算法,对于TD(1),每走一步,都把上一步的Q更新一次。

但是,这个基本算法是浪费了一些资源的。比如你走了ABCD4步,走B的时候可以更新A,走C的时候,其实可以把AB都更新一次,而且A可以用TD(2)更新,走D的时候,也完全可以再用TD(3)更新一次A。但是如果你每走一步都要遍历一次已走过的步,就会造成不同s-a对的更新次数不平衡,第一步的s-a对更新次数最多,而最后一步的s-a对只更新一次。
这里就要引入 S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)算法
考虑到我上面提到的资源浪费问题,可以对更新次数进行一个改动,保证一个s-a对只更新一次,又可以综合一定长度的步数。即把TD(1)到TD(n)的值利用资格迹衰减参数 λ \lambda λ综合起来,虽然每个回合只是对一个s-a对进行一次更新,但是这次更新利用了n次TD的结果:
![]()
比如ABCDEFGHI步,执行TD(3),走到D开始更新A,更新的时候用BCD分别对应TD(1),TD(2),TD(3)的综合Q来更新,同理,走到E更新B的时候,要用CDE三个TD值综合。
总之,Sarsa和Sarsa( λ \lambda λ)都是走一步就更新一个Q方格,而不用等到走完。
Q-learning:异策略时序差分控制
Sarsa是一种同策略算法,Q-learning是异策略算法。
总的来说,以策略算法分为目标策略和行为策略,目标策略可以理解为军师,完全理智,决定大方向,行为策略虽然按照大方向走,但是还是可能上头,做出随机的决定。可以说,目标策略是保守的,贪心的,行为策略具有不确定性,可以进行风险更大的探索。

在Sarsa中,不仅需要当前步SA,还需要下一步SA,即实际走出去的Action。而Q-learning中,只需要当前步SA与下一步S就行,为什么呢?因为每次优化策略后,一个s下的Action是固定的,只要知道下一个s,就可以通过Q表格知道下一步的Action。
那问题又来了,既然你不用走就知道下一步的Action,为什么Sarsa又要知道下一步的Action才能对这一步的Q进行优化呢?这是因为 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略使Action不完全由Q决定。加假如没有随机性,Sarsa和Q-learning就是一样的。有了随机性以后,Sarsa就有一种不放心下一步Action的感觉,非得下一步Action出来以后才能更新这一步Q,而Q-learning就很放心,不用下一步Action出来就可以更新Q,即使你实际上做出的行动和我预期不一样。
从效果上来说,Sarsa更胆小,Q-learning更激进。比如悬崖问题,t时刻你在s1,然后采取了down行为,走到了s2,这个时候Q-learning和Sarsa就有分歧了:
- Q-learning的目标策略认为在S2时刻,你一定会向右走,所以直接把Q值更新,很有可能是一个增大的Q值,因为距离终点更近。虽然实际上因为 ϵ − g r e e d y \epsilon-greedy ϵ−greedy可能走到悬崖里,但是已经和悬崖边的S1-down的Q值没有关系了,你走到悬崖边里只会让S2的Q值变小。当你下次走到S1的时候,S1-down的Q值仍然很大,S1仍然也会选择down策略。
- Sarsa不放心实际策略的执行,所以等S2选择了Action后才会更新S1的Q值。如果是S2-down,即S2的Q值很小,这就会导致S1-down的Q值变小,下一次走到S1的时候,很有可能就不会选择down策略了。
- 随着时间推进,Sarsa和Q-learning两种方法的优化效果会逐渐趋同,但是前期累积的差异已经无法扳回了

总的来说,Q-learning有一种不见棺材不掉泪的感觉,目标策略只负责大方向,不会过多约束行为策略,非得行为策略一步走到陷阱才会改进上一步的Q值(目标策略),但是Sarsa只要走到陷阱的附近就会改进上一步的Q值,甚至会有一种传递性(这也是图中Sarsa为什么要走最外面而不是中间层的原因),即Q-learning更加大胆,Sarsa比较胆小。
你可能觉得Sarsa不如Q-learning,但是实际上Sarsa是对Q-learning的改进,很多对安全性要求高的任务中,即使是牺牲一些效率也要保证安全,这就要用Sarsa,但是另一些任务,即使是发生失误也无所谓,就要极致的速度,那就用Q-learning。
关键概念
P,R的未知性导致了动态规划方法无法使用,只能使用蒙特卡洛衍生的方法。所以不需要每次策略改进就进行大量迭代,只需要走一回合/一步然后对部分Q表格进行增量式更新,然后基于Q表格做策略改进即可。
Q表格:横轴为动作,纵轴为状态(在python中应该是一个DataFrame,用[]选择一列)
评估:蒙特卡洛+时序差分
控制:Sarsa算法与Q-learning
策略梯度
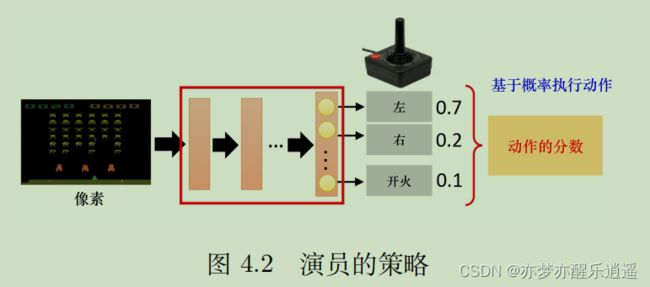
从现在开始,要脱离传统表格型方法,开始向DQN演化了。此后,强化学习的智能体称作演员(Actor)
强化学习中,环境和奖励函数(规则)不受控制,我们唯一能决定的就是Actor。
策略梯度算法理论
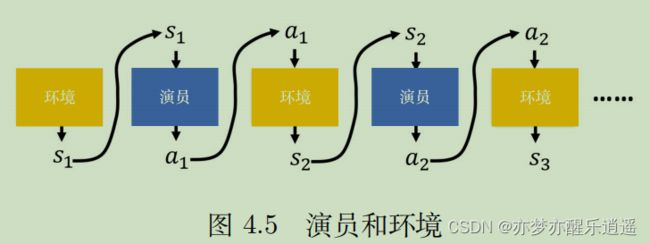
强化学习其实也可以用类似于RNN的网络训练。网络的输入是图片(观测矩阵),输出是动作的softmax(决策)。而网络本身,就是对策略的拟合。
训练的过程中,Actor和Env的交互如图所示。两者互为输入。
将上图抽象,则轨迹可以写成下面的数学形式:一连串的s-a对。
假设给定了策略(此处为 θ \theta θ),则一条轨迹的概率为:
下面这个公式本来应该写成条件概率,但是因为强化学习决策过程具有马尔科夫性质,所以概率条件不是s就是s-a对,不会更长了。
进一步将,P(a|s)是智能体,是我们能控制的,而p(s|s,a)代表环境,不是我们能控制的。
最后说一下奖励函数,r(s,a),给定sa,输出r。
给定一个轨迹,就可以计算出轨迹的奖励总和,不一定是累加,也可能是衰减累加,总之是总和,写作 R ( τ ) R(\tau) R(τ)
如何评价一个策略好不好,就需要用R函数了。如果对所有可能的轨迹进行概率加权求和,就可以得到对于一个策略的R期望。实际操作中,因为概率不明确,更多的是采用蒙特卡洛采样计算。总之可以得到一个R期望,其仅随 θ \theta θ改变。进一步改写一下形式,就变成了右边的概率论形式:R对于 θ \theta θ模型期望。
那回归强化学习,我们的目标就是通过不断优化策略(神经网络),让R期望(目标函数)越来越大,这是不是很像梯度下降?这里更应该说是梯度上升。
从梯度角度来说,我们要先计算目标函数的梯度。已知一个轨迹的R是固定的(不可微分),但是其概率随着 θ \theta θ改变,所以求导以后是对p求导。

将式子改进,基于4.6和4.7(TODO,4.6是为什么?),可以得到梯度的变式:
这个变式还是没法直接计算,因为p计算不了,所以使用蒙特卡洛采样的方法去近似替代。即,通过大量采样,得到的总样本计算出的频率就可以逼近概率。
当然,此处已经不用再去算频率了,直接加起来取平均就是期望的近似。(下图为取N次蒙特卡洛平均),解释一下这两个循环:
- 外层循环是对E的近似。通过大量采集轨迹去求得轨迹的期望
- 内层循环是对一个轨迹的分步求解。本来是 ∇ l o g p θ ( τ n ) \nabla log p_\theta (\tau^n) ∇logpθ(τn),然后因为轨迹的p实际上是所有步骤的累乘,最后被log作用后,累乘变累积加
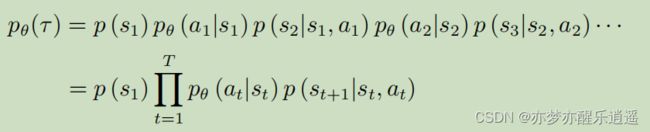
此处两个疑问:
- 在最右边的R应该是关于s-a的函数,这里看起来像是常数的样子(平均值)。姑且忽略即可,后面会优化,关联到每一步,其实就类似于Q函数。
- ∇ l o g p θ ( a t ∣ s t ) \nabla logp_\theta(a_t|s_t) ∇logpθ(at∣st)能求吗?概率怎么求导?首先要直到p是怎么算出来的。给定一个神经网络,输入s,输出a的softmax向量,这个softmax就是概率。在pytorch或者tensorflow框架中,只要是走神经网络顺着算出来的,就可以通过差分算出导数,所以理论上是完全可以计算的(实际求法各有千秋)。
- 为什么忽略初始p以及环境p,这是因为不可控制,在求和求导的过程中导数为0。
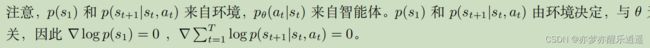
最后,直观地理解一下:
首先,给定s-a,R是确定的,如果R是正,最后的R梯度就会增大,如果R是负,这一项就是负的了,R梯度就会减小。因为R是确定的,所以如果想要梯度尽量大,那么就应该提高R正的p,降低R负的p,然后基于这个原则,去进行梯度上升调节,令R期望不断增大。
基于上面最后推导出的计算方法,强化学习的流程如下:
策略梯度实现技巧
添加基线
很多游戏中,奖励不小于0,那么根据前面推导,在优化过程中,所有的概率就都会向着增大的方向走,就会造成竞争,产生意料之外的后果。
那么在优化的过程中,因为最后要归一化,肯定不能是所有概率都增加,提高少的或者不提高的(没采样到),概率就会下降。这很明显对没采样到的就很不公平。所以要平衡采样到的奖励,不能让奖励都是正,即添加基线:
添加基线后,不管原先定义的奖励如何,修正后总会有正有负,这样对于没采样到的样本,就公平一些。
至于b如何设置,可以用R的期望。
分配合适的分数
我们前面提出一个疑问,为什么一个回合里所有s-a对的奖励的R(加权求和R)都是一样的,这很明显不合理,不能因为总体的R是好的,就让每一个s-a对的R都是好的。尤其是采样数量不够庞大的时候,这种统计结果并不具有说服力。
所以将不同s-a的奖励函数分开计算,此时这个计算方法就是前面的G函数,是一个s-a对真正的价值:
实际上,b是依赖于状态的,所以b其实可以通过另一个网络计算得出。综合来看,经过基线+分步修正后的R值,已经变成了(相对)优势函数 A θ ( s t , a t ) A^{\theta}(s_t,a_t) Aθ(st,at),那这么来看,其实优势函数(包括b),可以通过一个网络计算出来,这个网络就是评论员(critic)
REINFORCE:蒙特卡洛策略梯度算法实例
强化学习有蒙特卡洛和时序差分两种做法,这里仅仅介绍蒙特卡洛算法:REINFORCE,讲解其细节。
在REINFORCE中,必须走完一个回合才能更新一次。按照前面的公式来说,应该是先求R均值,再整体求导。但是下图伪代码却是一个回合更新T次。这是因为,这个式子的形式是相加的,所以其实对轨迹中的每一个状态分别求导,迭代T次,和你加起来一次性求导,迭代一次,效果是一样的(效率不同)。
同理,我们这里只跑了一次,所以N=1,但是你N次迭代叠加起来,基本相当于采样N条轨迹后直接整体求导(还有点区别,回合内T次更新,其样本是同分布的,但是更新一次后再采样一条轨迹,其实分布已经变了,不过姑且忽略就行)
这里给出一些细节:
计算G的时候,应当是从后往前计算,反正更新次序是无所谓的。而且是,如果每次更新都是针对一个s-a对更新的,那走一个完整的回合可以通过bp更新T次。
而如何进行自动求导bp呢,这需要联系深度学习的知识了。在深度学习中,是给定X和Y的,用 y ^ 和 y \hat{y}和y y^和y的交叉熵计算理论与实际的偏差,然后用优化器将这个偏差求导,降低。
在我们强化学习这里,没有标签。比如我这一步的输入为s,行为为a(输出),但是我们没有理想的行为,唯一能够评价行为好坏的就只有G函数。所以将交叉熵和G融合一下,先用输出的a概率向量与其对应的one-hot向量(代表实际的行动,一般的算法是取a向量中概率最大为1)求交叉熵,然后给交叉熵乘以G函数,代表其优秀程度。
这样的计算综合了预测与行动的差距以及行动的质量,可以作为损失的度量。
比如下图,输出概率向量=[0.02,0.08,0.9],one-hot向量=[0,0,1](假设用epsilon-greedy,也可能采用随机策略,就不一定和概率最大的对应了),求交叉熵后还要乘以G函数。然后丢进优化器进行bp。实际编程中,可以像上面提到的,一个回合内更新T次,也可以先对回合进行累加,最后对一个回合进行整体更新(这样对优化器负担比较小,个人感觉效率更高)。
到这里,其实又和前面联系回来了。上图中那个带G参数的交叉熵,结果算出来再求导后实际上就对应前面REAINFORCE算法的 G ∇ l n π ( A t ∣ S t , θ ) G\nabla ln\pi (A_t|S_t,\theta) G∇lnπ(At∣St,θ)部分。所以前面的一通理论,证明了这种方法的合理性以及可实现性。
具体到编程中,需要几个主要的函数:
- predict:根据S,从网络中得到a向量
- sample:根据a向量与策略(比如epsilon-greedy),获取实际行动的one-hot向量
- learn:通过带权重交叉熵,进行bp。
关键概念
-
策略。同前面
-
轨迹。trajectory,一系列s-a对构成
-
G与R。G是从一个状态开始,未来的总奖励函数。而R是相对于一个回合或者一个实验的,也是总奖励。最开始的策略梯度算法是将一个回合整体求平均的,但是这显然不公平,于是拆分,对每一步求一个G函数。实际上都是用G函数的。
-
REINFORCE:经典的策略梯度+蒙特卡洛算法,一回合更新一次(或者T小次)
近端优化算法(PPO)
深度Q网络(DQN)
传统Q-learning通过表格记录Q函数。而在很多任务中,比如CartPole,状态空间是连续的,此时可以通过函数逼近Q表格。而神经网络本身就可以看做一个复杂的函数,所以神经网络自然成了解决连续空间任务的方法。这种神经网络就叫Q网络。
虽然用Q网络替代了Q表格,但是训练的思路是一样的:采样,根据S-A计算Q函数,用新的Q函数值更新评论员(Q网络),新的网络应当计算出更大的Q值。用新的网络根据Q值继续采样,重新计算Q值,继续更新策略,让Q值越来越大。
总的来说,DQN有如下关键点:
- 价值函数近似
- 目标网络分离
- 经验回放
强化学习的本质
DQN我看了两遍,第一遍是有点迷惑的,书里的描述给我一种似是而非的感觉,第二次看,我终于看透了强化学习中Q表格,Q网络的本质,以及强化学习到底在学什么。我这里强调的东西,请牢记,不然后面可能看着看着就迷惑了:
强化学习的本质,是训练一个能客观评价环境的评论员,评论员给出S-A二元组的得分,我们始终是在训练Q网络(评论员)。训练过程就是通过不断地采样,试错。来获得对客观环境的信息,将其保存在Q网络中,不断优化,直到得到一个完全客观,Q值尽可能大的网络为止。
观察下面的公式,Q网络训练的效果是:让当前的Q趋近于r+后续最佳的Q。只要把Q函数训练好,就可以判断出任意S状态下最佳的action,这意味着,任意状态S下,只要每次step都采取最佳Q对应的action,就可以获取理想中的Q值,也就对应理想中的收益了。
至于策略,是根据已知信息决定的。比如epsilon-greedy,就是以一定概率采取最大Q值对应的行为,策略本身从始至终不变,只是用于决策的信息(Q表格)变了罢了。总之策略的原则是人制定的,是固定的。
所以说,无论是V迭代还是Q迭代,最终目标就是让V和Q值趋近于真实情况。所谓的寻找更好的策略,我认为有所偏颇,实际上是更好的评论员(环境建模)罢了,之所以叫新策略,是因为策略结果本身就是依赖于评论员的,评论员变好后,针对其评论结果而采取的行为会变好,看起来是行为变了,然而本质还是评论员变了。
网络近似
状态价值函数
这里的状态价值函数同前面表格型方法中的V函数。曾经的V函数,其参数为离散的S,现在的V函数也是以S为参数,只不过S是连续的了。
衡量V函数同样有蒙特卡洛和时序差分方法。
训练V函数的方法就是,先采样,然后对于一个状态都用实际的G函数作为标签,用输出的V函数作为预测,这样就变成了回归问题,可以进行bp调节了。最终的调节方向就是,让V越来越趋近于真实的G。
当V逐渐迭代,趋近于真实的G,收敛后,所有状态的价值就一目了然了。这个时候,我们就朝着V值更大的状态走就行了。
另一种是时序差分。
把这个公式变一下,用r作为实际值,用两个V的差作为预测,构成回归任务,进行bp调节。
蒙特卡洛方法和时序差分的本质区别在于方差。
直观来说,一局游戏有无数步,每一步都会积累一个偏差,这些偏差叠加起来,一次性进行回归,会造成很大的方差。而每一步进行一次回归,单步方差比较小,即使是所有步叠加,也不会很大。
更直观一点,蒙特卡洛的公式里没有以前的信息作为参照,只看现在,就像是,只要发生了,我就认定这就是对的。而时序差分公式里参考以前的信息,虽然发生了意料之外的事情,但是和以前有点不太一样,时序差分会带有怀疑的态度,直到反复发生以后才会认定。
从数学上来说,蒙特卡洛方法相当于在X里乘了k,求方差后就会出来一个 k 2 k^2 k2,而时序差分就像是先求方差,再乘k,这样蒙特卡洛的方差就是时序差分的k倍。所以时序差分是更常用的,因为更稳定。
动作价值函数
其实我个人认为,用Q函数更加科学。因为单单用状态去衡量回报有点粗略,虽然说形势大于人,但是人的决策还是会对回报产生巨大影响的,所以价值函数理应是s和a的二元函数。当然,采用了Q函数以后,还涉及到一个动作选择问题,不过是后话了。
Q函数的写法有两种,右边这种其实就是我们前面的表格型方法。一个状态对应A种action,每种action都有一个Q被同时输出。但是这种不适用于连续情况,因为不知道action有几种。所以实际上DQN用左边的方式。输入s-a,输出Q。
具体训练过程也很简单,如果你看懂了我在这章开头说的本质,就明白了我们实际上是要不断用时序差分/蒙特卡洛方法,让Q函数对现实环境的评价更加客观,当Q趋近于真实值,我们的策略针对Q采取的行动自然就是最佳的了。所谓的更好的策略,本质上还是更好的Q网络,Q网络是评论员,所以说策略自始至终没变,只是行为变了罢了。
至于给定Q网络,如何指定策略选择action,如果action是有限的,那么用argmax就可以得到策略,但是如果action是连续的,会有其他方法。
必备技巧
目标网络
Q网络是神经网络,就需要bp迭代,进一步说,就是要构建回归训练。如下图,预测值是左边,实际值是右边,理论上这两个是相等的,但是因为我们的Q网络刚开始对环境的建模不好,所以总是不等,所以就需要进行bp迭代。
如果用Q表格这么搞,没啥问题,但是做神经网络,能不能收敛是一个重要的问题。右边相当于label,一般来说对于一个输入,label都是不变的,但是Q网络一变,y和 y ^ \hat{y} y^都变了,即预测和标签都变了,网络很不稳定,这就很不好收敛。好比与一个猫在追老鼠,结果老鼠一直跑,自然就捉不到。
所以人们自然能想到把右边固定了,这就是目标网络。加了目标网络后,先把目标网络固定,然后采样迭代N次Q网络,再把参数复制到目标网络后,继续前面的迭代。用猫和老鼠的例子来说,就是先让老鼠停下一段时间,让猫去追一会,快追到以后再让老鼠跑开,然后老鼠停下让猫继续追。这样的次数多了以后,猫和老鼠的距离就会稳定地拉近。
探索
我们前面就介绍过epsilon-greedy策略,这是一种探索策略,为什么要探索呢?
这就像是我们人一样,如果一直待在舒适区不出来,你可能就失去了更好的机会。对于Q网络,如果走一个方向可以获得收益,但是别的方向还没走过,那么这个方向的收益就会一直大于另外的方向。又因为我们是以收益来决定方向的,所以每次都会朝着一个方向走,又会增大这个方向的收益。
为了解决探索-利用窘境(exploration-exploitation dilemma),可以采用epsilon-greedy或者玻尔兹曼探索。
epsilon-greedy已经介绍过
这里介绍玻尔兹曼探索。其实玻尔兹曼探索就类似模拟退火:
- T大,则Q的影响很小,所以更容易产生随机策略
- T小,则Q的影响变大,当T=1的时候,就由Q本身决定概率
- 当T趋近于0,那Q就起到决定性作用,Q大的一定会被执行
经验回放
首先定义什么是经验。
每次更新,都需要SARS这4个变量,所以把一组SARS作为一个经验。基于经验+经验缓冲区,可以形成经验回放机制。这个机制有什么用?
- 一般的强化学习都是采样一次,更新一次,一次只用一个经验,效率比较低。而神经网络训练通常是以batch为单位的,采用了经验回放后,就可以一次用一个batch去迭代。
- 此前,一个经验只能用一次就被丢弃,利用率太低,经验回放可以让一个经验被合理地重复利用。
具体的经验回放实现例子如下(假设缓冲区容量为5w):
- 使用当前Q网络,进行1次交互,存入缓冲区。如果缓冲区已满,则进行替换
- 从缓冲区中提取batch_size个经验,送入Q网络进行bp迭代
- 如果迭代了C次,则更新目标策略(目标Q网络)
从上面的过程可以看出,现在每次交互都可以用batch_size个样本去更新。这些经验来自于不同策略,有现在的策略,也有以前的策略,这其实已经是异策略了。就像我们平时从自己的行为中学习的时候,不仅仅是用当前的经验学习,还要参考以前的经验。这样做好处很多:
- 使用batch加快训练
- 重复利用以前的经验
- 丰富的异策略可以提高模型鲁棒性
DQN整体思路
关键概念
- DQN:用神经网络近似价值函数的强化学习方式,采用BP方式训练。DQN还结合了目标策略,经验回放的技巧。
- 状态价值函数(V),动作价值函数(Q)
- 目标网络:用于产生标签的网络,通常固定,定期置换
- 探索:epsilon-greedy和玻尔兹曼探索
- 经验回放:将不同策略的经验放在一个缓冲区中,每次迭代取一个batch,是一种异策略方法
DQN衍生技巧(Tricks of DQN)
Double DQN(DDQN)
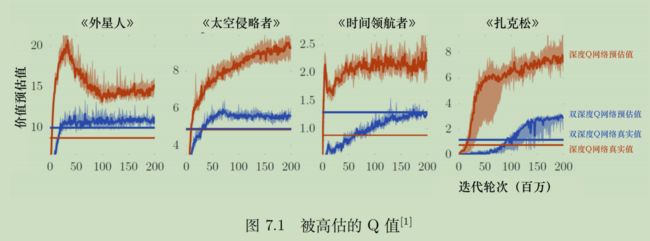
Q网络计算出的Q值,在训练过程中整体会随着对各种情况的探索而不断增大。但是就像人学习一样,刚开始啥也不知道,中间是知道一些,就开始膨胀,最后彻底明白了,才能放平心态。机器的训练是无法做到彻底明白的(无法穷举),那么这种策略必然会导致高估Q值(有一些隐藏的情况没有被探索到),估计的Q值高于实际获取的价值。
DDQN算法可以拉进估计值与真实值的距离。
从数学的角度来说,目标Q值的计算是会有误差的。假设目标有4个action,当前状态肯定要选择一个能使目标Q最大的action。问题就出在,假设第一个动作的实际Q值低于第二个动作,但是估计出来的Q值更大,那么当前状态就会选择第一个动作作为目标Q值的参数。
总之就是,无论哪一个动作被高估,我们总是会选择哪个高估的动作,所以就总是高估。从本质上来说,你使用max策略,要么就是真的选到了max,要么就是选到高估的,不可能选到低估的action。
在DQN的基础上修改。原来,选择action的网络是目标网络,但是我们DDQN使用可变的Q网络去选择action
那么结果无非是几种:
- 都没有高估
- 可变网络高估了,目标网络没高估。虽然选错了动作,但是目标网络给这个不好的动作打了低分,目标Q值也不会高估。
- 可变网络没高估,目标网络高估(假设b动作高估,a动作正常)。动作没选错(假设选了a),虽然目标网络b高估了,但是我不去算b,而是算a,仍然是正常的目标Q值。
- 可变网络和目标网络都高估。回归了DQN的错误情形。
由此可见,以前是55开的高估可能,现在高估可能只有26开了,提高了对高估的容错率。
实现起来也特别简单,改一下公式就可以,所以如果只能选一个技巧的话,就用DDQN就很方便。
深度竞争Q网络(dueling DQN)
基础Q网络,是输入S-A,得到标量Q,或者输入S,得到向量,对应所有action的Q向量。
深度竞争Q网络,不直接输出Q值,而是分成两路计算,一路计算一个V值,一路计算A向量。V值可以理解为一个状态的平均收益,类似于状态价值函数。而A值可以理解为在一个状态下,采取不同action对收益带来的波动。这个波动有正有负。
举个例子,下图给出4个状态下,A与V是如何生成Q的,符合前面的描述。
进一步看,加入把第二个状态的V从0变成1,那么第二个状态的Q向量整体就会加1。可见,V对Q的影响是整体性的。
这有什么用呢?首先,本身就是合理的。其次,如果每次迭代,主要是更新V值,那么就不需要采样S状态下所有的action就可以更新所有action的Q值,这样的效率更高,这也是这个方法的关键效果:加速。
其实这里有个隐含的问题。逻辑上合理,并不代表网络会朝着你期望的角度去发展。毕竟,如果最后V值恒等于0,那A不就和Q一样了吗?这种情况完全有可能出现。
为了防止这种情况出现,我们要给A加一个限制,即总和为0,直接给他归一化即可,均值归0,方差不变。下图展示了归一化过程。
优先级经验回放(PER,prioritized experience replay)
![]()
我们训练的方式是回归,如果预测和目标差距不大,那么相当于已经回归得不错了,没必要继续算下去了。
从经验的角度来看,就是这一笔经验已经没用了,无法对训练产生效果了,所以在从经验回放池中选择的时候,这种无用经验就可以放弃了,或者给一个较低的概率。反过来,如果差距大,那么这笔经验就有较大的训练价值,就应该给更大的概率,即优先权。
具体怎么实现呢?
首先,肯定是要修改那个sample函数。但是具体怎么做书里没说,我给一种思路:
- 假设最终要选batch_size个经验
- 我先随机选出k×batch_size个经验
- 然后把这些经验的Q值都算出来,并计算出与目标的差距
- 选差距最大的batch_size个,或者归一化后按照概率采样batch_size个
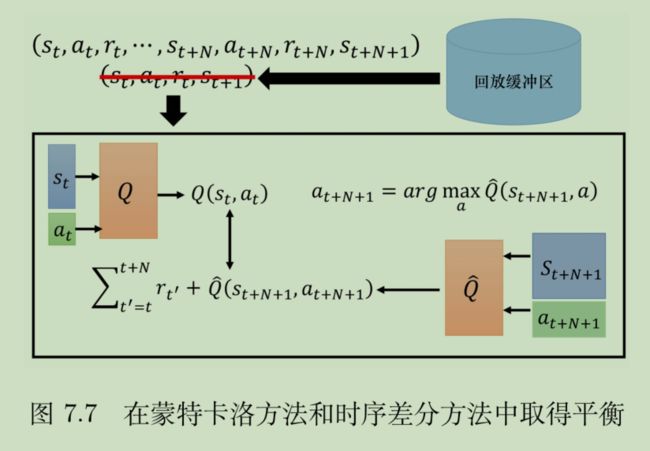
多步方法
蒙特卡洛好不好呢?其实蒙特卡洛算出来的Q值,是最真实的Q值,他的缺陷在于只认事实。在样本量不少的情况下,无异于以偏概全。但是如果样本量特别大呢?大量的事实累计起来,那就是非常客观的了。反过来,在数据量特别大的情况下,时序差分反而差点意思。
总的来说,就是数据量小,建议用时序差分来降低方差,数据量大,更建议用蒙特卡洛,在大数据的加持下,方差会落在合理范围内。那中间的呢?
可以调整。多步时序差分介于TD(1)与MTCS之间,N甚至可以作为超参数去调,适应数据量的多寡。
这个时候经验就要改一下了,存放的状态和累积奖励都应该变一下。同时,应该维持一个轨迹记忆,便于计算N步累积奖励。
噪声网络(noisy net)
- epsilon是给动作空间加噪声,就好像是,意外的不可抗力逼着你不得不采取某些策略(随机策略),即使你想要做预期的决策,最后也可能因为意外也无法落实。
- 噪声网络是在参数空间加噪声,扰动你对S-A的评估,你虽然是心想事成,但是这个决策可能压根就是误判。
epsilon和噪声网络还有一个区别:
- epsilon在每个step都会扰动一次。epsilon让智能体在任何时刻都是不稳定的。
- 噪声网络只会在episode开始施加,在episode内部是不变的。只有到了新的episode才会重新生成扰动。噪声网络就是,一个人在一段时间(一个回合)内,状态是稳定的,但是不同的时间段内,状态有所波动。
从效果上来说:
- epsilon的扰动比较混乱
- 噪声网络更加系统,对于同一个状态,就好像是这个回合向左试试,另一个回合向右试试。
这两种扰动孰优孰劣,难以比较,因为噪声网络刻画的是智能体的不稳定性,epsilon是环境的不稳定性。如果没有环境的不确定性,那么这种搜索就叫依赖状态的搜索(state-dependent exploration),即心想事成。
具体怎么做?
- OpenAI的方法比较简单。直接给所有参数都加一个规定均值方差的高斯噪声
- DeepMind方法更复杂。高斯噪声的参数还可以根据训练得到
但是无论如何,回合内噪声都是不变的。
分布式Q函数(distributed Q-function)
环境是有随机性的,奖励其实也应该具有随机性。可以说,即使是同一个S-A,在现实中的Q都是不一样的。涉及到了概率,原来的Q值可以理解为一个期望,那么实际上Q(S,A)应当是一个分布。
下图给出了两种概率分布,其均值相同,但是实际确实完全不同的分布,Q的意义也完全不同。如果简单的用标量衡量,就无法对环境的随机性建模。
![]()
如何给环境建模呢?或者说如何把Q值变成一个分布呢?理想情况应该是一个概率密度分布,但是实际上我们只能给出离散化的近似概率密度分布。
- 对于每一个S-A,可以把Q值的可能区间切分成k份。即,将Q网络的输出从n维向量变成n×k维向量。
- 比如就是-10到10,切成5份,以区域中心的值代表这个区域的均值,高度对应概率
修改了网络结构后怎么用呢?
- 可以用在action选择上,根据分布的方差来判断这个action的风险大不大。
- 至于Q值计算,其实还是用均值的,当然,也可以用分布去采样一个S-A对应的Q值。
从具体实现来讲,不是特别好实现,比如你怎么确定那个区间?我的想法是,先用普通方法训练一次,把训练过程中的Q均值画成曲线,然后估计一下,再用分布式训练。
彩虹(RainBow is All You Need)
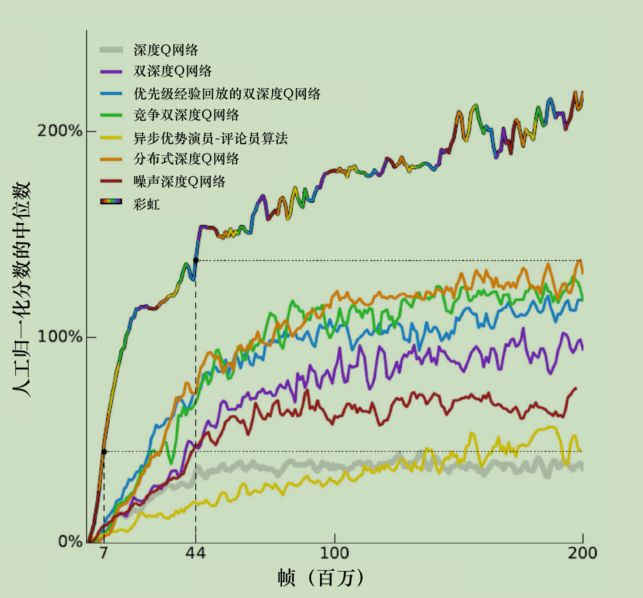
我们前面说的各种技巧,包括后面会出现的异步优势演员-评论员算法(asynchronous advantage actor-critic,A3C),实际上互不冲突,可以分布在不同的阶段。
那么全部用上,就是RainBow了,效果特别好,比基础DQN能翻好几倍性能。
上图只是RainBow和其他方法的对比,那RainBow中,各个方法的重要性有没有个主次?
去掉一种方法,去比较性能,得到下图,有一些特殊的结论:
- 分布计算,多步计算,优先级经验回放,噪声都挺重要的,深度竞争也有点用。
- 去掉了DDQN反而不影响精度,这说明有一种其他机制替代了DDQN的作用。
DDQN核心作用是防止高估,而分布式计算通过限制区间,已经人为杜绝了高估和低估的可能性。