模块2 模式识别系统
模块2 模式识别系统
2.1 模式识别的基本概念
特征与特征空间
样本到特征空间的转换
我们把一个个用于识别的具体事物称为样本。
如果我们抽取出样本能够用于识别的某个重要特性就称为样本的一个“特征”
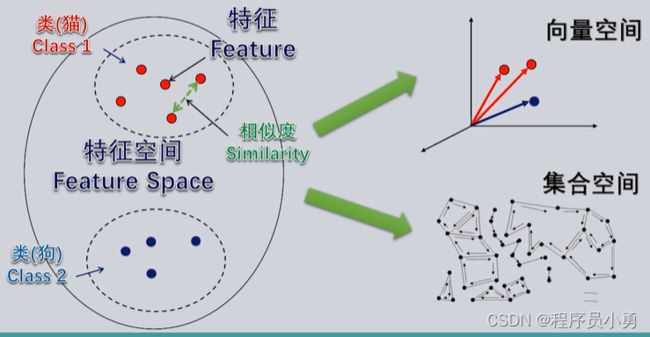
所有的样本转换为特征表达后,它们的整体就够了一个空间,我们称为”特征空间“
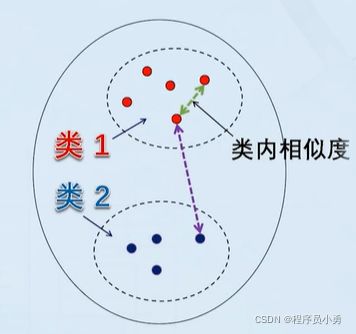
在特征空间中,每个样本都可以看作是一个由一组特征来表达的一个点,而样本之间的相似程度,可以用这些特征空间的点之间的相似程度来计算
特征空间中属于同一类事物样本的点,也会聚集在一起,就形成了特征空间中的“类”的概念
不同类型的特征空间
(1)向量空间
如果样本用于识别的每一个特征,可以作为一个向量空间的一个维度,那么一个样本抽象到特征空间中就成为一个向量,也就是向量空间中的一个点。此时,样本与样本之间的相似度,就可以用向量空间中定义的某种“距离”来度量,而每一类样本的聚集区域,则表现为向量空间中点的统计分布
(2)集合空间
如果从样本中抽取出的特征不能用向量空间来表达,则可以构成一个集合空间,此时样本的相似度计算,需要用其他方式来定义。如果我们抽取的特征是样本某些方面结构特征,显然,样本与样本之间的相似性,会表现为结构关系或拓扑关系上的相似性,这就不是距离可以表达的了
有监督学习与无监督学习
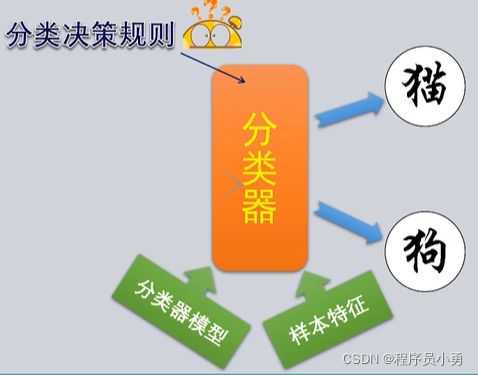
模式识别的核心是一个分类器
当我设计好一个分类器时,它可以将待识别的样本归类到某一个类别中,也就识别出了这个样本是什么
分类的依据:样本的特征(包括每一类样本的共同特征)、分类决策规则(如何根据样本的特征做归类的判决)
最好的方式是计算机能够自动去找到分类决策规则,从自然规律中去发现该如何对样本进行归类
分类的训练(学习)
要实现一个好的分类器,我们首先要确定分类决策规则的框架(分类的模型或模式识别的算法),以及究竟从样本中抽取哪些特征用于分类,然后我们才能让这个分类器运作起来,并通过它自身的学习去找到最好的分类器模型参数(或分类决策规则的参数),从而实现模式识别的功能
在已经确定分类器模型和样本特征的前提下,分类器通过某些算法找到自身最优参数的过程,就称为分类器的训练,也常常从人工智能第一人称的角度称为分类器的“学习”
从总体上,分类器学习到分类决策规则有两种不同的模式:有监督学习和无监督学习
-
有监督学习
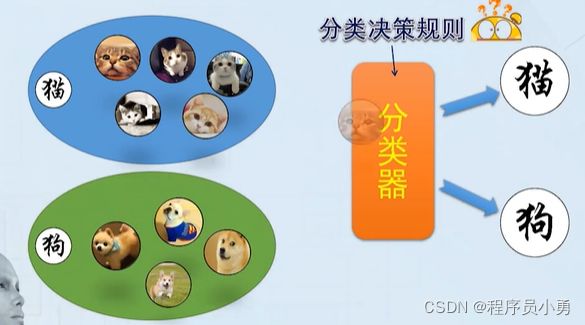
如果我们对于每一个类别,都给定一些样本,这样就形成了一个具有类别标签的训练样本集。
分类器可以通过分析每一个样本,去寻找属于同一类的样本具有哪些共同的特征,也就是从训练集中学习到具体的分类决策规则,这称为有监督学习
-
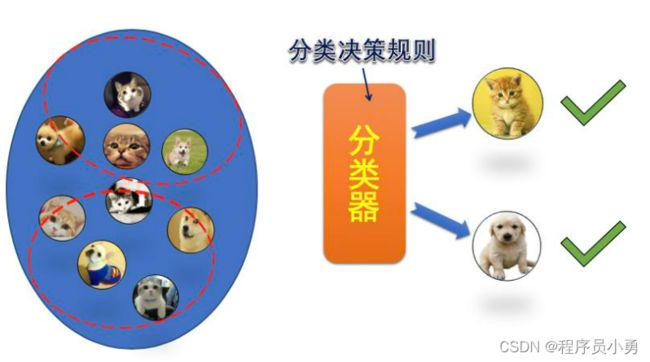
无监督学习
根据相似程度的大小,我们可以按照一些规则,把相似程度高的样本作为同一类,从而将训练样本集的样本划分为不同的类别,再从每一个类别的样本中去寻找共同的特征,形成分类决策规则,就完成了分类器学习的任务。这种没有使用类别标签的训练集进行分类器学习的模式,就称为“无监督学习”。
紧致性与维数灾难
紧致性准则
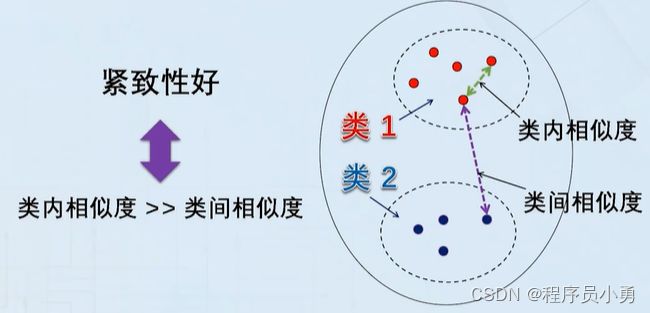
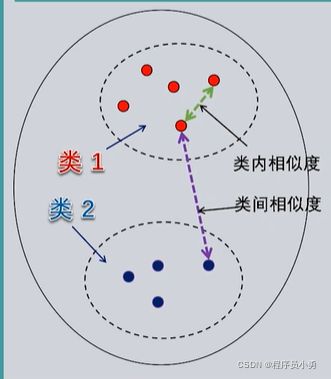
如果同类样本之间的相似度越大,不同类样本之间的相似度越小,分类决策规则的裕量也就越大,无论是在分类器学习还是在分类器用于对具体样本进行分类时,发生错误的可能性也就越小。这可以作为评判用于有监督学习的带标签训练样本集,以及作为无监督学习结果的样本集优劣的一个指标,称为“紧致性”准则。即:紧致性好的样本集,样本的类内相似度远大于类间相似度
如何计算相似度?
距离
a)正定性: d ( x i , x j ) > 0 , ( i ≠ j ) , d ( x i , x x ) = 0 d(x_{i},x_{j})>0,(i≠j),d(x_{i},x_{x})=0 d(xi,xj)>0,(i=j),d(xi,xx)=0
b)对称性: d ( x i , x j ) = d ( x j , x i ) d(x_{i},x_{j})=d(x_{j},x_{i}) d(xi,xj)=d(xj,xi)
c)传递性: d ( x i , x j ) ≤ d ( x i , x l ) + d ( x l , x j ) d(x_{i},x_{j})≤d(x_{i},x_{l})+d(x_{l},x_{j}) d(xi,xj)≤d(xi,xl)+d(xl,xj)
满足标准的距离定义非常多,在向量空间中,就可以定义欧氏距离、曼哈顿距离、切比雪夫距离。非向量空间中也可以定义距离,例如两个字符串之间的编辑距离,也是一种合法的距离定义
非距离的相似度
余弦相似度: c o s θ = x T y ∥ x ∥ ⋅ ∥ y ∥ cos\theta =\frac{x^{T}y}{\left \| x \right \|\cdot \left \| y \right \|} cosθ=∥x∥⋅∥y∥xTy
皮尔逊相关系数 p x , y = c o v ( x , y ) δ x δ y p_{x,y}=\frac{cov(x,y)}{\delta x\delta y} px,y=δxδycov(x,y)(cov为协方差)
维数灾难
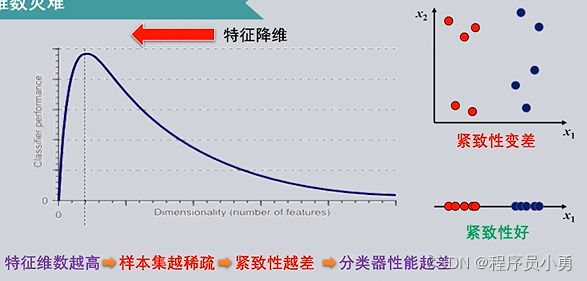
只要不断地增加模式识别问题中的特征维度,很快我们就会遇到一个巨大的问题,被称为维数灾难
维数灾难指当一个问题描述的维度不断增加时,会带来计算量剧增与解法性能下降等严重问题。
导致维数灾难的根本原因,在于训练集样本数量的不足。
要解决维数灾难的问题,就要尽可能提升每一个维度在分类中的效能,从而使模式识别问题能够在较低维度下得到更好的解决。
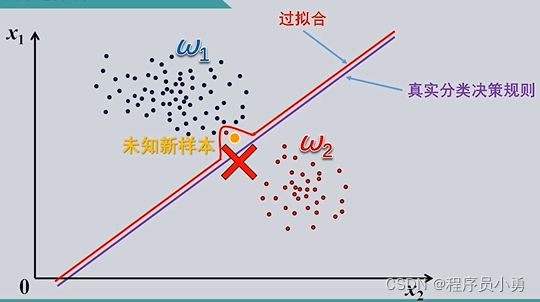
泛化能力与过拟合
分类器的泛化能力
我们期望的是分类器能够从训练样本集中发现所要分类的各个类别的特点,即找到一个最优的分类器,使得它经过训练后,不仅能将训练集中的样本正确分类,而且对于不在训练姐中的新样本,也能够正确地分类。这种训练好的分类器对未知样本正确分类的能力,就称为“泛化能力”
分类器的过拟合
由于过分追求训练样本集中样本的分类正确性,导致的分类器泛化能力降低,称为分类器训练过程中的“过拟合”
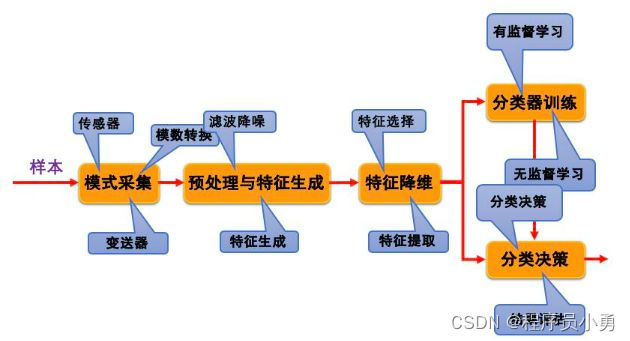
模式识别系统
模式识别系统的组成
在这个系统中,待识别的样本经过模式采集,取得相应的信息数据,这些数据经过预处理环节,生成可以表征模式的特征,特征降维环节从这些特征中选取对分类最有效的特征,在分类器训练环节得到最优的分类器参数,建立相应的分类决策规则,也可以说是设计出一个有效的分类器,最后在分类器已设计好的情况下对待识别的单个样本进行分类决策,输出分类结果。
(1)模式采集
模式识别研究的是计算机识别,因此事物所包含的各种信息必须通过采集转换成计算机能接受和处理的数据。对于各种物理量,可以通过传感器将其转变为电信号,再由信号变换部件对信号的形式、量程等进行变换,最后经A/D采样转换成对应的数据值
(2)预处理
经过模式采集获得的数据量,是待识别样本的原始信息,其中可能包含大量的干扰和无用的数据。预处理环节通过各种滤波降噪措施,降低干扰的影响,增强有用的信息,在此基础上,生成在分类上具有意义的各种特征
预处理生成的特征可以仍然用数值来表示,也可以用拓扑关系、逻辑结构等其他形式来表示
(3)特征降维
从大量的特征中选取出对分类最有效的有限的特征,降低模式识别过程的计算复杂度,提高分类准确性,是特征降维的主要任务
特征降维的主要方法包括特征选择和特征提取。
特征选择是从已有的特征中,选择一些特征,抛弃其他特征
特征提取是对原始的高维特征进行映射变换,生成一组维数更少的特征
(4)分类器设计
分类器设计过程就是分类器学习的过程,或者说是对分类器进行训练的过程。分类器设计是由计算机根据样本的情况自动进行的,可分为有监督学习和无监督学习
(5)分类决策
分类决策是对待分类的样本按照已建立起来的分类决策规则进行分类,分类的结果要进行评估
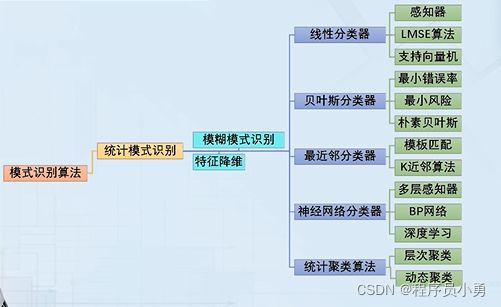
2.2 模式识别的算法体系
统计模式识别是主流的模式识别方法,它是将样本转换成多维特征空间中的点再根据样本的特征取值情况和样本集的特征值分布情况确定分类决策规则。
线性分类器是最基本的统计分类器,它通过寻找线性分类决策边界来实现特征空间中的类别划分。
贝叶斯分类器也是统计分类器,它的分类决策规则是基于不同类样本在特征空间中的概率分布,以逆概率推理的贝叶斯公式来得到类别划分的决策结果。
最近邻分类器把学习过程隐藏到了分类决策过程中,通过寻找训练集中与待分类样本最相似的子集来实现分类决策
神经网络分类器来源于对生物神经网络系统的模拟,它的本质是高度非线性的统计分类器,并且随着计算机技术的发展从浅层网络向深度学习不断演化,目前已成为新一轮人工智能热潮的基础
聚类分析是无监督学习的典型代表,目前采用统计学习方法
模糊识别不是一套独立的方法,而是将模糊数学引入模式识别后,对现有算法的模糊化改造,它在更精确描述问题和更有效地得出模式识别结果方面都有许多有价值的思路
特征降维也不是独立的模式识别算法,但是是完成模式识别的流程中不可缺少的一个步骤
结构模式识别与统计模式识别有根本性的不同,它抽取的不是一系列数值型的特征,而是将样本结构上的某些特点作为类别和共同的特征,通过结构上的相似性来完成任务
句法模式识别利用了形式语言理论中的语法规则,将样本的结构特征转化为句法类型的判定,从而实现模式识别的功能。聚类分析中,也可以采用结构特征上的相似性来完成样本类别的划分
2.3 第一个模式识别算法实例
问题:手写数字识别
作为分类问题的手写数字识别
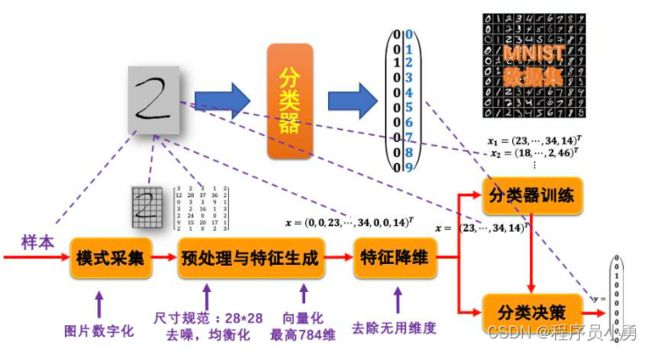
分类器的输入是一张包含单个数字的图片,输出为1个10维向量,有且只有1维为1,其他维为0,表示输入样本将会被唯一地分类到一个类别中,也就是被唯一地识别为某一个数字。
输入的样本是一个含有手写数字的图片,模式采集是将它数字化,成为一个二维的像素矩阵,每个像素都有其颜色或灰度值。
预处理首先会对样本对应的数字化二维图片进行缩放,统一到一个规定的尺寸,使得像素矩阵的维数固定,在这一实例中我们使用28*28的尺寸。然后会对图片进行去噪、均衡化等预处理,使得图片中有关手写数字的信息更加突出。在特征生成环节,可以从图片中提取轮廓、颜色分布、关键点等特征,也可以直接将二维矩阵展开为1维向量作为特征,所以特征的维度最高位784维。
特征降维主要是去除无用特征维度,选取有用维度。对手写数字识别这一问题,因为维度整体不高(最高784维),所以在某些算法里可以不经过特征降维,直接进行后续的训练和分类,有的算法会进行简单的降维,去除对类别区分没有价值的维度。
分类器训练需要一个训练集。我们会采用多种数据集,既包括著名的公开公开手写数字数据集MNIST,也包括我们自建的一个手写数字数据集。
算法:从模板匹配开始
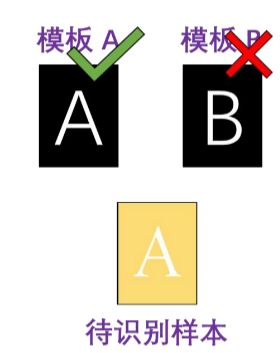
模板匹配的基本原理:为每个类别建立一个或多个标准模板,分类决策时将待识别的样本与每个类别的模板进行比对,根据与模板的匹配程度将样本划分到最相似的类别中。
模板匹配算法直接、简单,在类别特征稳定、明显,类间差距大的时候可以使用。但是它在建立模板的时候需要依赖人的经验和观察,适应能力会比较差。
用模板匹配实现数字识别
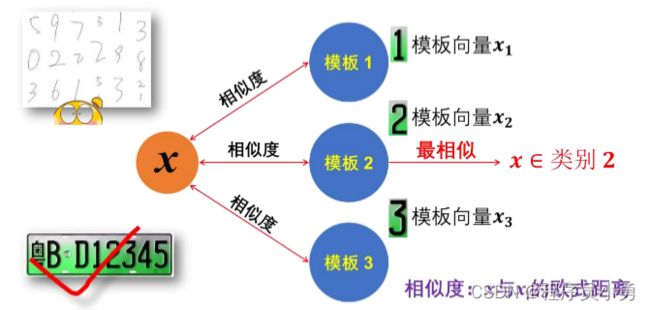
如果我们要采用模板匹配实现数字识别,我们首先要给每个类别确定一个模板,然后根据待识别样本与模板之间的相似度大小,将其划分到最相似的模板对应的类别中。
模板也应当以以上的784维向量来设定。而样本的特征向量与模板的特征向量之间的相似度,可以用欧氏距离来计算。
2.4 算法实例演示-模板匹配
% mat2vector.m
% 输入:图片数据(矩阵),样本个数
% 函数作用:将图片组转化为行向量,每个行向量作为一张图片的特征
% 输出:样本数*图片像素大小的矩阵
function[data_] = mat2vector(data, num)
[row, col, ~] = size(data);
data_ = zeros(num, row * col);
for page = 1: num
for rows = 1: row
for cols = 1: col
data_(page, ((rows-1) * col + cols)) = im2double(data(rows, cols, page));
end
end
end
end
% Template_hand.m
% 手写数字模板
clear all
clc
%读取模板
image = cell(1, 10);%生成十个cell保存模板
for i = 0: 9
filename = sprintf('../手写/%d/2.bmp', i)
image{1, i + 1} = mat2vector(imresize(imread(filename), [28, 28]), 1);%与车牌数据处理相同
end
%待匹配样本
correct_num = 0;
for index = 0: 9%每个数字测试一次
distance = zero(1, 10);%保存计算得到的距离值
fname = sprintf('../手写/%d/4.bmp', index);
sample = mat2vector(imresize(imread(fname), [28, 28]), 1);%图片转换为行向量
for j = 1: 10 %共十个模板,计算与每个模板的距离
distance(j) = pdist2(sample, image{1, j}, 'eucliean');
%计算欧氏距离,这里可以改为‘eucliean’为其他距离
end
[m, p] = min(distance);%计算距离最小值,并给出索引
if p - 1 == index
correct_num = correct_num + 1;
end
fprintf('数字%d到模板的最小距离为:%d,匹配到的类别为:%d\n',[index, m, p - 1]);%打印匹配结果
end
fprint('共测试10个样本,正确匹配个数为%d个\n', [correct_num]);
% Template_car.m
% 车牌数字模板匹配
% 读取10张模板0-9,由于本身是bmp,读到之后矩阵元素为unit8
% 需要转换为double方便计算
% 原图像大小不一致,并且维度较高,这里将所有的模板均重置为25*25
clear all
clc
image = cell(1, 10);%生成十个cell保存模板
for i = 0: 9
filename = sprintf('../车牌/%d.bmp', i)%读取模板文件
image{1, i + 1} = mat2vector(imresize(imread(filename), [28, 28]), 1);
%统一大小,之后调用函数将其转换为行向量
end
% 车牌数据
% 待匹配的样本,一样处理为25*25double类型
correct_num = 0;
for index = 0: 9%每个数字测试一次
distance = zero(1, 10);%保存计算得到的距离值
fname = sprintf('../车牌/%d.1.bmp', index);
sample = mat2vector(imresize(imread(fname), [28, 28]), 1);%图片转换为向量
for j = 1: 10 %共十个模板,计算与每个模板的距离
distance(j) = pdist2(sample, image{1, j}, 'eucliean');
%计算欧氏距离,这里可以改为‘eucliean’为其他距离
end
[m, p] = min(distance);%计算距离最小值,并给出索引
if p - 1 == index
correct_num = correct_num + 1;
end
fprintf('数字%d到模板的最小距离为:%d,匹配到的类别为:%d\n',[index, m, p - 1]);
% 索引从1开始,模板从0开始
end
fprint('共测试10个样本,正确匹配个数为%d个\n', [correct_num]);