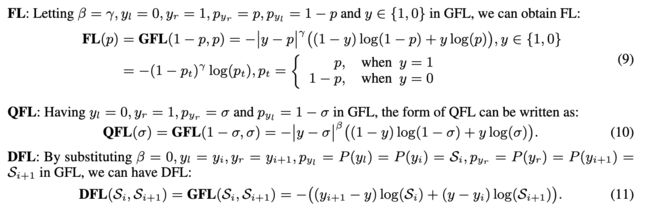Generalized Focal Loss：Focal loss魔改以及预测框概率分布，保涨点 | NeurIPS 2020

为了高效地学习准确的预测框及其分布，论文对Focal loss进行拓展，提出了能够优化连续值目标的Generalized Focal loss，包含Quality Focal loss和Distribution Focal loss两种具体形式。QFL用于学习更好的分类分数和定位质量的联合表示，DFL通过对预测框位置进行general分布建模来提供更多的信息以及准确的预测。从实验结果来看，GFL能够所有one-stage检测算法的性能
 
来源：晓飞的算法工程笔记 公众号

论文: Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection

• 论文地址：https://arxiv.org/abs/2006.04388
• 论文代码：https://github.com/implus/GFocal

Introduction

---

  目前，dense detector(one-stage)是目标检测中的主流方向，论文主要讨论其中的两个做法：

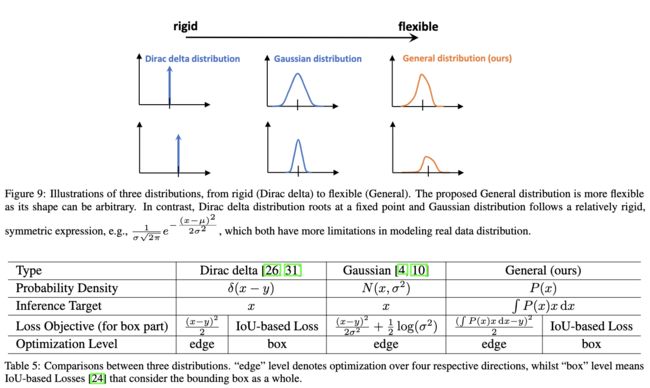
• 预测框的表示方法(representation)：可认为是网络对预测框位置的输出，常规方法将其建模为简单的Dirac delta分布，即直接输出位置结果。而有的方法将其建模为高斯分布，输出均值和方差，分别表示位置结果和位置结果的不确定性，提供额外的信息。

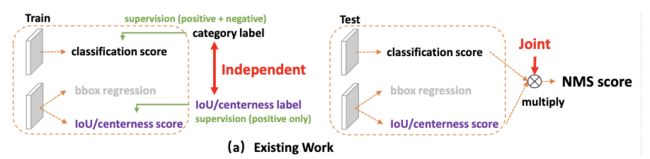
• 定位质量估计：最近一些研究增加了额外的定位质量预测，比如IoU-Net加入了IoU分数的预测和FCOS加入了centerness分数的预测，最后将定位质量以及分类分数合并为最终分数。

  经过分析，论文发现上述的两个做法存在以下问题：

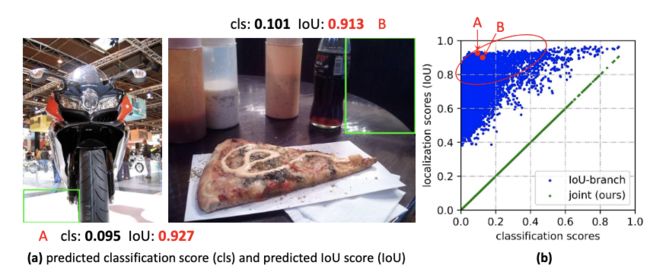
• 定位质量估计和分类分数实际不兼容：首先，定位质量估计和分类分数通常是独立训练的，但在推理时却合并使用。其次，定位质量估计只使用正样本点进行训练，导致负样本点可能估计了高定位质量，这种训练和测试的差异会降低检测的性能。
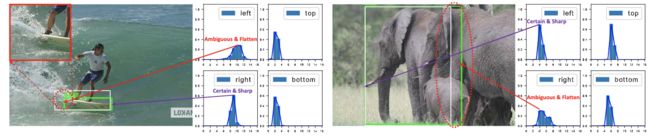
• 预测框表示方法不够灵活：大多算法将其建模为Dirac delta分布，这种做法没有考虑数据集中的歧义和不确定部分，只知道结果，不知道这个结果靠不靠谱。虽然有的方法将其建模为高斯分布，但高斯分布太简单粗暴了，不能反映预测框的真实分布。

  为了解决上面的两个问题，论文分别提出了解决的策略：

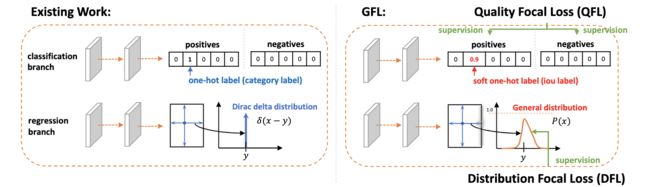
• 对于定位质量估计，论文将其直接与分类分数进行合并，保留类别向量，每个类别的分数的含义变为与GT的IoU。另外，使用这种方式能够同时对正负样本进行训练，不会再有训练和测试的差异。

• 对于预测框的表示方法，使用general的分布进行建模，不再强加任何的约束，不仅能够获得可靠和准确的预测结果，还能感知其潜在的真实分布情况。如上图所示，对于存在歧义或不确定的边界，其分布会表现为较平滑的曲线，否则，其分布会表示为尖锐的曲线。

  实际上，使用上述提到的两种策略会面临优化的问题。在常规的one-stage检测算法中，分类分支都使用Focal loss进行优化，而Focal loss主要针对离散的分类标签。在论文将定位质量与分类分数结合后，其输出变为类别相关的连续的IoU分数，不能直接使用Focal loss。所以论文对Focal loss进行拓展，提出了GFL(Generalized Focal Los)，能够处理连续值目标的全局优化问题。GFL包含QFL(Quality Focal Los)和DFL( Distribution Focal Los)两种具体形式，QFL用于优化难样本同时预测对应类别的连续值分数，而DFL则通过对预测框位置进行general分布的建模来提供更多的信息以及准确的位置预测。
  总体而言，GFL有以下优点：

• 消除额外的质量估计分支在训练和测试时的差异，提出简单且高效的联合预测策略。
• 很好地对预测框的真实分布进行灵活建模，提供更多的信息以及准确的位置预测。
• 在引入额外开销的情况下，能够提升所有one-stage检测算法的性能。

Method

---

Focal Loss (FL)

  FL主要用于解决one-stage目标检测算法中的正负样本不平衡问题：

  包含标准的交叉熵部分$-log(p_t)$以及缩放因子部分$(1-p_t{)}^{\gamma }$，缩放因子会自动将容易样本降权，让训练集中于难样本。

Quality Focal Loss (QFL)

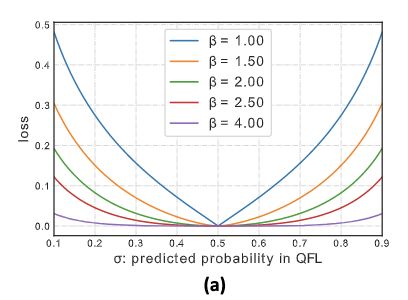
  由于FL仅支持离散标签，为了将其思想应用到分类与定位质量结合的连续标签，对其进行了扩展。首先将交叉熵部分$-log(p_t)$扩展为完整形式$-((1-y)log(1-\sigma )+ylog(\sigma ))$，其次将缩放因子$(1-p_t{)}^{\gamma }$泛化为预测值$\sigma$与连续标签$y$的绝对差值$|y-\sigma {|}^{\beta }$，将其组合得到QFL：

  $\sigma =y$为QFL的全局最小解。

  缩放因子的超参数$\beta$用于控制降权的速率，表现如上图所示，假定目标连续标签$y=0.5$，距离标签越远产生的权重越大，反之则趋向于0，跟FL类似。

Distribution Focal Loss (DFL)

  论文跟其它one-stage检测算法一样，将当前位置到目标边界的距离作为回归目标。常规的方法将回归目标$y$建模为Dirac delta分布，Dirac delta分布满足${\int }_{-\infty }^{+\infty }\delta (x-y)dx=1$，可通过积分的形式求得标签$y$：

  如前面说到的，这种方法没有体现预测框的真实分布，不能提供更多的信息，所以论文打算将其表示为general的分布$P(x)$。给定标签$y$的取值范围$[y_0,y_n]$，可像Dirac delta分布那样从建模的genreal分布得到预测值$\hat{y}$：

  为了与神经网络兼容，将连续区域$[y_0,y_n]$的积分变为离散区域$\{y_0,y_1,\cdots ,y_i,y_{i+1},\cdots ,y_{n-1},y_n\}$的积分，离散区域的间隔$\Delta =1$，预测值$\hat{y}$可表示为：

  $P(x)$可通过softmax操作$\mathcal{S}(\cdot )$获得，标记为${\mathcal{S}}_i$，预测值$\hat{y}$可使用常规的方法进行后续的end-to-end学习，比如Smooth L1、IoU loss和GIoU Loss。

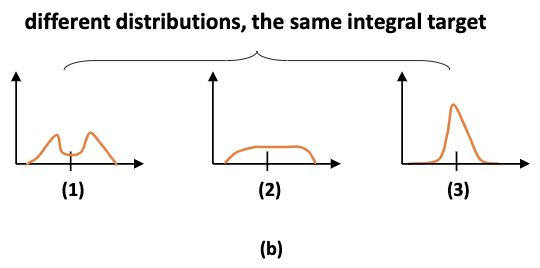
  但实际上，同一个积分结果$y$可由多种不同分布所得，会降低网络学习的效率。考虑到更多的分布应该集中于回归目标$y$的附近，论文提出DFL来强制网络提高最接近$y$的$y_i$和$y_{i+1}$的概率，由于回归预测不涉及正负样本不平衡的问题，所以DFL仅需要交叉熵部分：

  DFL的全局最优解为${\mathcal{S}}_i=\frac{y_{i+1}-y}{y_{i+1}-y_i}$，${\mathcal{S}}_{i+1}=\frac{y-y_i}{y_{i+1}-y_i}$，使得$\hat{y}$无限接近于标签$y$。

Generalized Focal Loss (GFL)

  QFL和DFL可统一地表示为GFL，假定值$y_l$和$y_r$的预测概率分别为$p_{y_l}$和$p_{y_r}$，最终的预测结果为$\hat{y}=y_l{p}_{y_l}+y_r{p}_{y_r}$，GT标签为$y$，满足$y_l\le y\le y_r$，将$|y-\hat{y}{|}^{\beta }$作为缩放因子，GFL的公式为：

  GFL的全局最优在$p_{y_l}^{\ast }=\frac{y_r-y}{y_r-y_l}$，$p_{y_r}^{\ast }=\frac{y-y_l}{y_r-y_l}$。

  FL、QFL和DFL均可认为是GFL的特殊情况。使用GFL后，与原来的方法相比有以下不同：

• 分类分支的输出直接用于NMS，不用再进行两分支输出合并的操作
• 回归分支对预测框的每个位置的预测，从原来的输出单个值变为输出$n+1$个值

  在使用GFL后，网络损失$\mathcal{L}$变为：

  ${\mathcal{L}}_{\mathcal{B}}$为GIoU损失

Experiment

---

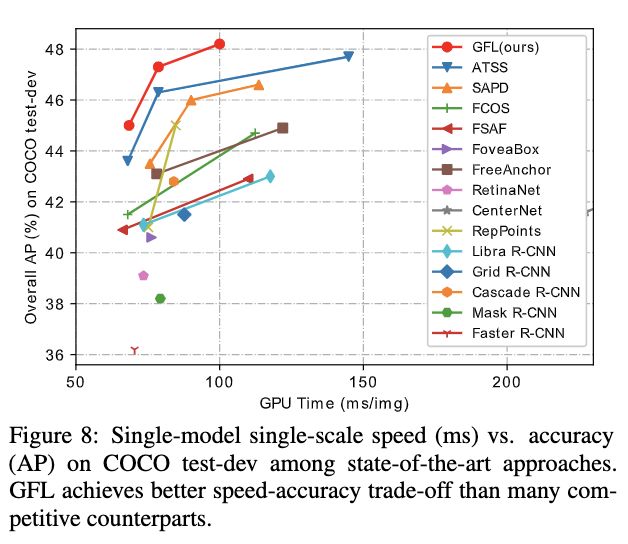
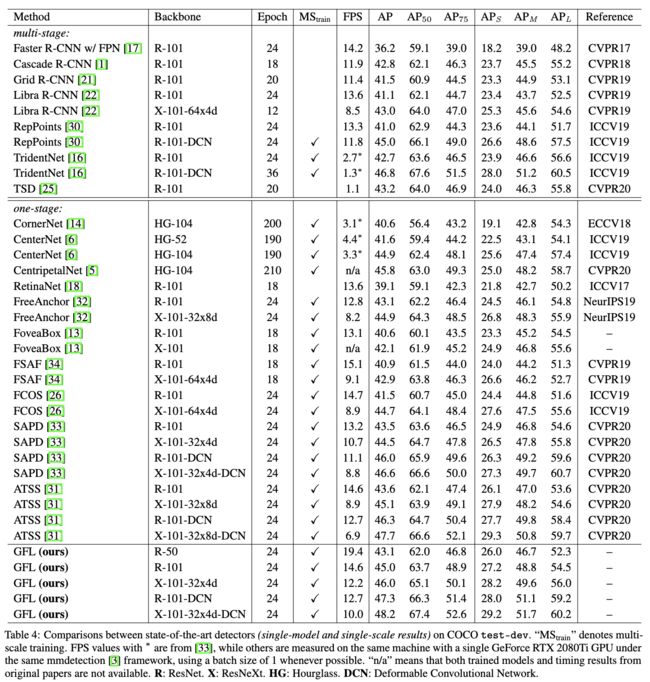
  性能对比。

  对比实验。

  基于ATSS与SOTA算法进行对比。

Conclusion

---

  为了高效地学习准确的预测框及其分布，论文对Focal loss进行拓展，提出了能够优化连续值目标的Generalized Focal loss，包含Quality Focal loss和Distribution Focal loss两种具体形式。QFL用于学习更好的分类分数和定位质量的联合表示，DFL通过对预测框位置进行general分布建模来提供更多的信息以及准确的预测。从实验结果来看，GFL能够所有one-stage检测算法的性能。

 
 
 

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】