机器学习 day1

书籍链接：http://tangshusen.me/Dive-into-DL-PyTorch/#/
一、线性回归
对于「线性模型」的内容，那我们就来看看「西瓜书」「统计学习方法」「ESL」「PRML」这几本书大概是怎么来讲解这部分内容的。
（1）「西瓜书」
「西瓜书」在第三章中展开了对「线性模型」的讨论，首先是介绍了线性模型「基本形式」，无论是线性回归还是线性分类，都是基于这个基本的线性模型的形式而来。
然后，「西瓜书」介绍了在「基本形式」的基础上，如何来构建「一元线性回归」问题的目标函数，其中的关键点在于如何衡量模型输出的预测值y_hat与数据真实的真实label值y的差距。这里「西瓜书」默认使用了均方误差的距离估计指标，但是我们要知道这并不是唯一的选择。在构建好「一元线性回归」的目标函数后，我们就可以来尝试进行求解了。我们的目标是找到对应的w和b使得我们minE()的目标实现，而这里介绍了一种解析解的求法，也就是最小二乘法。
在介绍完一元的情况后，「西瓜书」开始介绍多元的情景，这里值得注意的是（3.10）与（3.11）之间的那个XTX的满秩假设或者正定假设通常是不成立的，因此实际上我们需要在这个地方加入正则化方法，这种方法在我们面对最优化问题的时候也非常常用。
接着，「西瓜书」开始讲解「线性分类」模型。也就是所谓的对数几率回归（log odds），通常我们也称其为logistic regression，但是要知道这与逻辑毫无关系。逻辑回归的形式其实在3.2节最后的广义线性模型那里就有了铺垫，实际上线性回归和逻辑回归在模型形式上的区别是，

可以看到就是y的形式的区别，而为什么是这样的形式，主要是和最大熵和拉格朗日乘数有关，这里就不具体介绍了。
关键在于我们在确定模型之后如何来构建对应的目标函数，这里采用了「最大似然」的思想。在目标函数确定之后，「西瓜书」又介绍了一种不同于「解析解」的「数值解」的方法。
最后「西瓜书」还介绍了线性模型的LDA的形式，他的模型和目标函数都有所不同。以及如何将而分类问题扩展到多分类的情况。最后还介绍了如何处理类别不平衡的问题。这是「西瓜书」的内容。

（2）「统计学习方法」
李航老师的「统计学学习方法」则是分别在第一张、第二章和第六章涉及到了线性模型的内容。
在第二章中，主要是对「感知机」这种线性分类模型的研究。首先依旧是先确定模型的形式，对应于「西瓜书」3.2的广义线性模型，然后在2.2.2部分讲解模型的求解策略，即如何构建目标函数。这里其实是是用了函数间隔的方法来构建目标函数。
然后就是讲解具体的学习参数的算法。首先介绍了原始形式下的随机梯度下降法（算法2.1），并且给出了算法收敛性的证明，这里可以根据例2.2来帮助理解这一算法。接着又介绍了对偶形式下的学习算法（算法2.2），可以通过例2.2来辅助理解。
第六章则涉及到了逻辑回归的问题。首先是是介绍了logistic distribution 的基本概念，以及如何使用它来构建分类模型。然后在6.1.3讲解如何是用「极大似然」的方法来构建目标函数，以及如何求参数。
6.2节则是介绍了logistic regression形式的一些由来，即关于最大熵问题的讨论，之后有机会的话给大家介绍一下如何从最大熵中推导出逻辑回归模型。6.3节则主要是介绍数值解的方法。这部分是「统计学系方法」的内容。

（3）「PRML」
「PRML」也就是我们经常说的模式识别与机器学习（Pattern Recognition and Machine Learning）这本书了，非常经典的一本贝叶斯视角的教材，李航老师的「统计学系方法」也参考了这本书的很多讲法。此外，于此对比的是「MLAPP」这本书，也是非常经典的机器学习教材，不过采用的是频率派的视角，可以与「PRML」对照着看。
「PRML」在1.5节、第三章和第四章中都有涉及到对线性模型的讨论。
其中1.5节主要是介绍了一些构建目标函数的思想，以及解决分类问题的三种方式。尽管我们一般用的比较多的还是判别式模型的方法，但是了解判别式方法和生成式模型的方法，以及它们分别的优劣势，对于我们掌握分类问题还是有很大帮助的。
第三章则是主要讲线性回归模型，与上述的两本教材不同，「PRML」在一开始就引入了「基函数」的概念（其他的教材大多是在SVM那一章节再引入），然后在基函数的概念下来构建模型。在讨论目标函数时，「PRML」对于最大似然方法和最小二乘方法之间的相互转换（看是否是高斯分布），并且给出了这两种不同方法分别如何进行求解。
而对于我们之前提到的XTX接近非满秩的情况或接近奇异矩阵的情况，「PRML」在不使用正则化的前提下提出可以使用SVD的方法来求解。当然「PRML」也没有错过对于正则化方法的介绍，这部分内容集中在3.1.4，介绍了不同的正则化项。3.1.5则主要是在处理多目标输出的情形。
3.3, 3.4 和3.5主要讲解贝叶斯下的线性回归。这一章的内容主要是为了解决如何确定合适的模型复杂度的问题。实际上最大化似然函数并不能够很好的解决这一问题，因为总会产生过于复杂的模型和过拟合现象。一种解决方式是是用独立的额外数据能够用来确定模型的复杂度（1.3节），搞定模型的超参，但是这需要较大的计算量。因此在这个地方「PRML」转而考虑线性回归的贝叶斯方法，这会避免最大似然的过拟合问题，也会引出使用训练数据本身确定模型复杂度的自动化方法。
在第四章节则是线性分类模型。依旧是二分类问题与多分类问题下的模型设置，以及最小平方方法为什么不适用于二分类问题（实际上这点在我们讲解最大似然和最小二乘的相互转化中就有提到，因为二分类问题显然不是高斯分布）。然后介绍不同的判别函数，比如Fisher判别函数和感知器的例子。
4.2主要介绍概率生成模型在分类问题上的应用，以及如何使用最大似然的方法来确定模型参数。4.3则是介绍概率判别式模型，这种方法使用了一般线性模型的函数形式，然后使用最大似然来直接确定参数（而不是从线性函数的softmax变换中取得）。4.5则是讲解贝叶斯logistic回归的内容。
这是「PRML」的部分。

（4）「ESL」
最后是「ESL」也就是统计学习基础（The Elementsof Statistical Learning）这本书。吐槽一下，这本书哪里基础了。。。
「ESL」中讲解的东西就更多了，其中比较有代表性的是它突出了L1范数的正则化方法，也就是所谓的lasso回归（L2正则化的叫岭回归）。实际上大家还可以去看看弹性网络之类的方法，综合了L1和L2，也非常有意思。
然后推荐一些相关的参考资料吧，因为其实lasso回归的一些算法已经推广到广义回归模型了（最小角回归）。
其中一个经典的解法就是偏最小二乘由， Wold (1975)提出，收缩方法的比较可以在 Copas (1983)和 Frank and Friedman (1993)中找到。
最小角回归过程由 Efron et al. (2004)等人提出；与这有关的是早期 Osborne et al. (2000a)和 Osborne et al. (2000b)的homotopy过程。向前逐步准则在 Hastie et al. (2007)中进行了讨论。
Park and Hastie (2007)发展了类似用于广义回归模型的最小角回归的路径算法。
一些文献：
Efron, B., Hastie, T., Johnstone, I. and Tibshirani, R. (2004). Least angle regression (with discussion), Annals of Statistics 32(2): 407–499.
Osborne, M., Presnell, B. and Turlach, B. (2000a). A new approach to variable selection in least squares problems, IMA Journal of Numerical Analysis 20: 389–404.
Osborne, M., Presnell, B. and Turlach, B. (2000b). On the lasso and its dual, Journal of Computational and Graphical Statistics 9: 319–337.
Hastie, T., Taylor, J., Tibshirani, R. and Walther, G. (2007). Forward stagewise regression and the monotone lasso, Electronic Journal of Statistics 1: 1–29.
Park, M. Y. and Hastie, T. (2007). l 1 -regularization path algorithm for generalized linear models, Journal of the Royal Statistical Society Series B 69: 659–677.
Wold, H. (1975). Soft modelling by latent variables: the nonlinear iterative partial least squares (NIPALS) approach, Perspectives in Probability and Statistics, In Honor of M. S. Bartlett, pp. 117–144.
Copas, J. B. (1983). Regression, prediction and shrinkage (with discussion), Journal of the Royal Statistical Society, Series B, Methodological 45: 311–354.
Frank, I. and Friedman, J. (1993). A statistical view of some chemometrics regression tools (with discussion), Technometrics 35(2): 109–148.

此外，实践中需要需要注意的是
偏置参数一般是1*1,的，如果改变一下批量的大小，这个线性层就不好使了，所以不会这样定义偏置。

二、softmax函数
1.softmax公式的得出方法大概解释可以解释为：
首先假设样本与理论标准函数的误差（类似于线性回归那一章中生成数据时叠加上的高斯误差）服从正态分布（高斯分布），并且不同样本之间独立同分布，通过贝叶斯公式计算各个分类的概率，将高斯分布的公式带入公式之后化简得到。
在一些地方softmax函数又被称为归一化指数（normalized exponential）

2.softmax函数和sigmoid函数
softmax和其他模型最与众不同的特点就是softmax函数了，那么为什么选softmax函数呢？
softmax函数是来自于sigmoid函数在多分类情况下的推广，他们的相同之处：
①.都具有良好的数据压缩能力是实数域R→[ 0 , 1 ]的映射函数，可以将杂乱无序没有实际含义的数字直接转化为每个分类的可能性概率。
②.都具有非常漂亮的导数形式，便于反向传播计算。
③.它们都是 soft version of max ，都可以将数据的差异明显化。

相同的，他们具有着不同的特点，sigmoid函数可以看成softmax函数的特例，softmax函数也可以看作sigmoid函数的推广。
①.sigmoid函数前提假设是样本服从伯努利 (Bernoulli) 分布的假设，而softmax则是基于多项式分布。首先证明多项分布属于指数分布族，这样就可以使用广义线性模型来拟合这个多项分布，由广义线性模型推导出的目标函数即为Softmax回归的分类模型。
②.sigmoid函数用于分辨每一种情况的可能性，所以用sigmoid函数实现多分类问题的时候，概率并不是归一的，反映的是每个情况的发生概率，因此非互斥的问题使用sigmoid函数可以获得比较漂亮的结果；softmax函数最初的设计思路适用于首先数字识别这样的互斥的多分类问题，因此进行了归一化操作，使得最后预测的结果是唯一的。

3.softmax 函数性质：
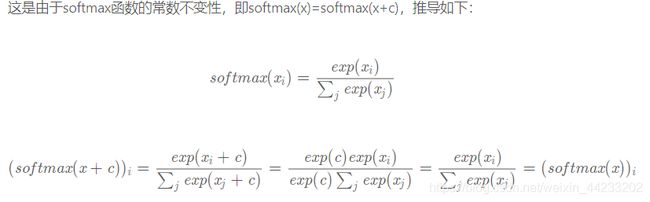上面的exp之所以可以消除，是因为exp(a+b)=exp(a)*exp(b)这个特性将exp提取出来了。
在计算softmax概率的时候，为了保证数值稳定性（numerical stability），我们可以选择给输入项减去一个常数，比如x的每个元素都要减去一个x中的最大元素。当输入项很大的时候，如果不减这样一个常数，取指数之后结果会变得非常大，发生溢出的现象，导致结果出现inf。

4.交叉熵
https://zhuanlan.zhihu.com/p/35709485

三、多层感知机
激活函数的选择
sigmoid的梯度消失是指输入值特别大或者特别小的时候求出来的梯度特别小，当网络较深，反向传播时梯度一乘就没有了，这是sigmoid函数的饱和特性导致的。ReLU在一定程度上优化了这个问题是因为用了max函数，对大于0的输入直接给1的梯度，对小于0的输入则不管。
但是ReLU存在将神经元杀死的可能性，这和他输入小于0那部分梯度为0有关，当学习率特别大，对于有的输入在参数更新时可能会让某些神经元直接失活，以后遇到什么样的输入输出都是0，Leaky ReLU输入小于0的部分用很小的斜率，有助于缓解这个问题。

四、文本预处理
文本预处理（常见，基础，不同任务特性不同预处理）
1、读入文本
2、分词
3、建立字典
4、将文本从词的序列转换为索引序列

#建立字典，设置阈值
#去重筛选词，特殊需求token
#1、count_corpus统计词频，得到counter
#2、增删，利用空列表
#pad:二维矩阵长度不一，短句子补token利用pad
#bos:开始token
#eos：结束token
#unk：未登录词当作unk

四、语言模型
n元语法

n元语法导致的问题：
参数空间过大：与n是指数变化关系
数据稀疏：
齐夫定律：语料库中单词的词频和单词出现的频率成反比
所以大部分的词，或词组在与语料库中根本不会出现，导致大部分词计算的概率为0，所以对概率的估计很不精确。

五、RNN
RNN介绍：https://www.bilibili.com/video/av13260183?p=2
循环神经网络使用相邻采样的时候为什么要detach参数。
我们知道相邻采样的前后两个批量的数据在在时间步上是连续的，所以模型会使用上一个批量的隐藏
状态初始化当前的隐藏状态，表现形式就是不需要在一个epoch的每次迭代时随机初始化隐藏状态，那么
根据上面所说的。假如没有detach的操作，每次迭代之后的输出是一个叶子节点，并且该叶子节点的
requires_grad = True，也就意味着两次或者说多次的迭代，计算图一直都是连着
的，因为没有遇到梯度计算的结束位置，这样将会一直持续到下一次隐藏状态的初始化。所以这将会导致
计算图非常的大，进而导致计算开销非常大。而每次将参数detach出来，其实就是相当于每次迭代之后虽然是
使用上一次迭代的隐藏状态，只不过我们希望重新开始，具体的操作就是把上一次的输出节点的参数requires_grad
设置为False的叶子节点。

我们知道循环神经网络的梯度反向传播是沿着时间进行反向传播的，而时间是不会停止的，所以我们会每隔一段时间、
进行一次反向传播，而我们这里的一段时间其实指的就是时间步，我们希望每间隔时间步之后进行一次反向传播，这样
来减小在梯度反向传播时带来的计算开销以及一定程度上缓解梯度消失或者爆炸的问题