Towards Open World Detection
Towards Open World Detection(OWOD)
2021 cvpr;
K J Joseph†‡, Salman Khan;
澳大利亚国立大学;
{cs17m18p100001,vineethnb}@iith.ac.in
Code: https://github.com/JosephKJ/OWOD
- 介绍
- 大背景
- 已有的工作
- 解决问题的方法
- 方法
- 对比聚类
- 用RPN给未知实例打上标签
- 避免遗忘
- 代码
- 实验
- 增量学习不同阶段的数据集
- 实验结果
- 指标
- 表格
- 图
介绍
大背景
现有的目标检测工作基于一个重要的前提假设:训练时网络应该见过所有的类别。本文放松这个假设条件为:
- 测试图像中可能包含未知的目标,应该被分类为“未知”;
- 网络能持续地学习新类。
OWOD (Open world object detection)将这个问题阐述为:先将未知任务识别为“未知”,然后再序列地接收额外信息来认识这些未知任务,即增量学习未知任务。
已有的工作
没有Open world object detection问题,但是有Open Set这个问题(分类/检测)。
Scheirer et al. [ 57] formalises this as OpenSet classification problem. Henceforth, various methodolo-gies (using 1-vs-rest SVMs and deep learning models) has been formulated to address this challenging setting. Ben-dale et al. [ 3] extends Open Set to an Open World classifi-cation setting by additionally updating the image classifierto recognise the identified new unknown classes
- 与open set分类问题不一样:目标检测的训练网络会把未知的目标当做背景;
- 与open set检测问题不一样:不能增量地学习目标检测。
解决问题的方法
- 开放世界对象检测,它对现实世界进行了更紧密的建模。
- 提出了一种基于对比聚类的未知感知网络和基于能量的未知识别方法,称为ORE (Open World Object Detector)。
方法
Open World Object Detection定义为:
- t t t 代表时刻
- K t = { 1 , 2 , . . , C } K^t = \{1,2,..,C\} Kt={1,2,..,C} 表示 C C C个已知类别的集合
- U = { C + 1 , . . . } U = \{C+1,...\} U={C+1,...} 表示未知类别的集合,可能会被inference
- D t = { X t , Y t } D^t = \{X^t, Y^t \} Dt={Xt,Yt} 表示数据与标签的配对
- X t = { I 1 , … , I M } X^{t}=\left\{I_{1}, \ldots, I_{M}\right\} Xt={I1,…,IM}, Y t = { Y 1 , … , Y M } Y^{t}=\left\{Y_{1}, \ldots, Y_{M}\right\} Yt={Y1,…,YM}, M M M张图像
- 每张图像中有 k k k 个实例 Y i = { y 1 , y 2 , . . , y k } Y_i = \{y_1,y_2,..,y_k\} Yi={y1,y2,..,yk},
- y k = [ l k , x k , y k , w k , h k ] \boldsymbol{y}_{k}=\left[l_{k}, x_{k}, y_{k}, w_{k}, h_{k}\right] yk=[lk,xk,yk,wk,hk], l k l_{k} lk是类别号,其余是框的坐标。
- K t + 1 = K t + { C + 1 , … , C + n } K_{t+1}=K_{t}+\{C+1, \ldots, C+n\} Kt+1=Kt+{C+1,…,C+n},下一个时刻的已知类别
一个成功的开放世界对象检测方法应该能够识别未知的实例,而且不会忘记以前认识的实例。
神经网络有很强的拟合能力,不同类的其latent space表示如果能区别大一点有两点好处:
- 更容易使已知和未知类区别出来,所以对比聚类对未知任务识别有促进作用;
- 使新学习的类和已学习的类的空间不容易重合。
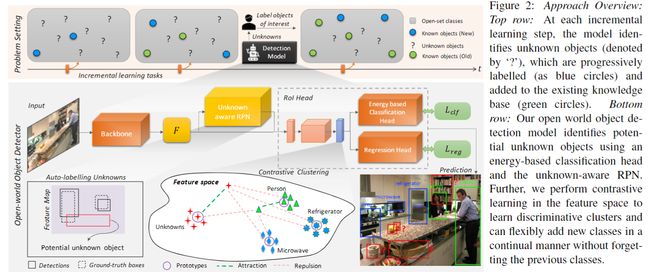
由于不能手动标注哪些实例是未知的,所以设计了一个自动识别未知类的方法来提供后续需要的label。因此需要使用基于Region Proposal Network的方法,获得候选框之后根据未知实例的亥姆霍兹自由能更高的特性来区分未知实例。
Faster-RCNN是一个二级目标探测器。在第一阶段,一种与类别无关的区域提议网络(RPN)从来自共享骨干网的特征映射中提出可能具有对象的潜在区域;第二阶段,对每个提议区域的边界框坐标进行分类和调整。对比聚类由感兴趣(ROI)头部区域的残差块生成的特征计算。RPN和分类头分别适用于自动标记和识别未知类别。
对比聚类
在潜空间中,类分离将是开放世界方法论识别未知类的理想特征。
建模为对比聚类问题,其中同一类的实例将被强制保持在较近的位置,而不同类的实例保持较远位置
对每一个类别 i i i,保持一个原型向量 p i p_i pi,目标检测器对每一个类别产生一个向量 f c f_c fc,定义对比损失函数为:
L cont ( f c ) = ∑ i = 0 C ℓ ( f c , p i ) \mathcal{L}_{\text {cont }}\left(\boldsymbol{f}_{c}\right)=\sum_{i=0}^{\mathrm{C}} \ell\left(\boldsymbol{f}_{c}, \boldsymbol{p}_{i}\right) Lcont (fc)=i=0∑Cℓ(fc,pi)
其中,
ℓ ( f c , p i ) = { D ( f c , p i ) i = c max { 0 , Δ − D ( f c , p i ) } otherwise \ell\left(\boldsymbol{f}_{c}, \boldsymbol{p}_{i}\right)= \begin{cases}\mathcal{D}\left(\boldsymbol{f}_{c}, \boldsymbol{p}_{i}\right) & i=c \\ \max \left\{0, \Delta-\mathcal{D}\left(\boldsymbol{f}_{c}, \boldsymbol{p}_{i}\right)\right\} & \text { otherwise }\end{cases} ℓ(fc,pi)={D(fc,pi)max{0,Δ−D(fc,pi)}i=c otherwise
D \mathcal{D} D表示任意一个距离函数,类内距离越小越好,类间距离越大越好。
每一类对应的特征向量的平均值被用来建立类原型特征集: P = { p 0 ⋯ p C } \mathcal{P}=\{p_{0} \cdots p_\mathrm{C}\} P={p0⋯pC},保持每个原型向量是ORE的重要组成部分。由于整个网络是端到端训练的,类原型也应该是逐渐演化的,因为组成特征是逐渐变化的(随机梯度下降在每次迭代中更新权值一小步)。
为每个类维护一个队列 q i q_i qi,全部类储存为: F store = { q 0 ⋯ q C } \mathcal{F}_{\text {store }}=\left\{q_{0} \cdots q_{\mathrm{C}}\right\} Fstore ={q0⋯qC}
用RPN给未知实例打上标签
计算对比损失的时候,目标检测器产生的向量 f c f_c fc, c ∈ { 0 , 1 , . . , C } c \in \{0,1,..,C \} c∈{0,1,..,C},其中0表示未知类。这就需要未知类的标签。
输入一张图像,RPN可能会将前景和背景的实例框选出来,并给出可能性得分。作者选择不和已知的ground truth的目标重合top-k得分的背景区域候选框作为未知目标的候选框,给与标签为0。
给定潜在空间 F F F中的特征 ( f ∈ F f \in F f∈F) 及其对应的标号 l ∈ L l \in L l∈L,学习能量函数 E ( F , L ) E(F,L) E(F,L)。基于能量模型[27],作者设计式子估计观察变量 F F F和可能的输出变量集 L L L之间的兼容性。
具体地说,作者使用亥姆霍兹自由能公式,其中将 L L L中所有值的能量组合在一起,
E ( f ) = − T log ∫ l ′ exp ( − E ( f , l ′ ) T ) E(f)=-T \log \int_{l^{\prime}} \exp \left(-\frac{E\left(f, l^{\prime}\right)}{T}\right) E(f)=−Tlog∫l′exp(−TE(f,l′))
其中T是温度参数。在Softmax层之后的网络输出和类别特定能量值的吉布斯分布之间存在简单的关系[34]。这可以用公式表示,
p ( l ∣ f ) = exp ( g l ( f ) T ) ∑ i = 1 C exp ( g i ( f ) T ) = exp ( − E ( f , l ) T ) exp ( − E ( f ) T ) p(l \mid \boldsymbol{f})=\frac{\exp \left(\frac{g_{l}(\boldsymbol{f})}{T}\right)}{\sum_{i=1}^{\mathrm{C}} \exp \left(\frac{g_{i}(\boldsymbol{f})}{T}\right)}=\frac{\exp \left(-\frac{E(\boldsymbol{f}, l)}{T}\right)}{\exp \left(-\frac{E(\boldsymbol{f})}{T}\right)} p(l∣f)=∑i=1Cexp(Tgi(f))exp(Tgl(f))=exp(−TE(f))exp(−TE(f,l))
其中 p ( l ∣ f ) p(l \mid \boldsymbol{f}) p(l∣f)是标签 l l l的概率密度, g l ( f ) g_{l}(\boldsymbol{f}) gl(f)是分类头 g ( . ) g(.) g(.)的第 l l l个分类数值。利用这种对应关系,作者根据分类模型的逻辑定义自由能如下:
E ( f ; g ) = − T log ∑ i = 1 C exp ( g i ( f ) T ) E(f ; g)=-T \log \sum_{i=1}^{\mathrm{C}} \exp \left(\frac{g_{i}(f)}{T}\right) E(f;g)=−Tlogi=1∑Cexp(Tgi(f))
上述方程为作者提供了一种将标准的faster R-CNN的分类头转换为能量函数的自然方法。
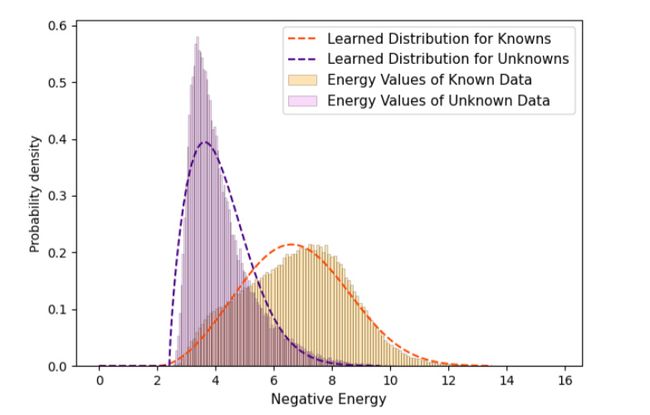
由于作者在潜在空间中强制与对比聚类有明显的分离,所以作者看到已知类数据点和未知数据点在能级上有明显的分离,如下图所示:
根据这一趋势,作者用一组移位的威布尔分布来模拟已知和未知能量值 ξ k n ( f ) \xi_{k n}(f) ξkn(f) 和 ξ u n k ( f ) \xi_{u n k}(f) ξunk(f) 的能量分布。与伽玛分布、指数分布和正态分布相比,这些分布能很好地拟合一个保持的验证集的能量数据。如果 ξ k n ( f ) < ξ u n k ( f ) \xi_{k n}(f)<\xi_{u n k}(f) ξkn(f)<ξunk(f),则学习的分布可用于将预测标记为未知。
避免遗忘
在增量学习中,贪婪的样本选择策略一致地比最先进的方法有更大的优势。
在Wang[62]等人的目标检测设置中,存储少量样本和重放的有效性已经被发现是有效的。
作者存储一组平衡的样本,并在这些样本上的每个增量步骤之后对模型进行微调。在每个点上,作者确保样本集中至少有每个类的 N e x N_{ex} Nex个实例。
代码
GeneralizedRCNN(
(backbone): ResNet(
(stem): BasicStem(
(conv1): Conv2d(
3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
)
(res2): Sequential(
(0): BottleneckBlock(
(shortcut): Conv2d(
64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv1): Conv2d(
64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
(conv2): Conv2d(
64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
(conv3): Conv2d(
64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
)
(1): BottleneckBlock(
(conv1): Conv2d(
256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
(conv2): Conv2d(
64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
(conv3): Conv2d(
64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
)
(2): BottleneckBlock(
(conv1): Conv2d(
256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
(conv2): Conv2d(
64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=64, eps=1e-05)
)
(conv3): Conv2d(
64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
)
)
(res3): Sequential(
(0): BottleneckBlock(
(shortcut): Conv2d(
256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv1): Conv2d(
256, 128, kernel_size=(1, 1), stride=(2, 2), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv2): Conv2d(
128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv3): Conv2d(
128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
)
(1): BottleneckBlock(
(conv1): Conv2d(
512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv2): Conv2d(
128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv3): Conv2d(
128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
)
(2): BottleneckBlock(
(conv1): Conv2d(
512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv2): Conv2d(
128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv3): Conv2d(
128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
)
(3): BottleneckBlock(
(conv1): Conv2d(
512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv2): Conv2d(
128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=128, eps=1e-05)
)
(conv3): Conv2d(
128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
)
)
(res4): Sequential(
(0): BottleneckBlock(
(shortcut): Conv2d(
512, 1024, kernel_size=(1, 1), stride=(2, 2), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
(conv1): Conv2d(
512, 256, kernel_size=(1, 1), stride=(2, 2), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv2): Conv2d(
256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv3): Conv2d(
256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
)
(1): BottleneckBlock(
(conv1): Conv2d(
1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv2): Conv2d(
256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv3): Conv2d(
256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
)
(2): BottleneckBlock(
(conv1): Conv2d(
1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv2): Conv2d(
256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv3): Conv2d(
256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
)
(3): BottleneckBlock(
(conv1): Conv2d(
1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv2): Conv2d(
256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv3): Conv2d(
256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
)
(4): BottleneckBlock(
(conv1): Conv2d(
1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv2): Conv2d(
256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv3): Conv2d(
256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
)
(5): BottleneckBlock(
(conv1): Conv2d(
1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv2): Conv2d(
256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=256, eps=1e-05)
)
(conv3): Conv2d(
256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=1024, eps=1e-05)
)
)
)
)
(proposal_generator): RPN(
(rpn_head): StandardRPNHead(
(conv): Conv2d(1024, 1024, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(objectness_logits): Conv2d(1024, 15, kernel_size=(1, 1), stride=(1, 1))
(anchor_deltas): Conv2d(1024, 60, kernel_size=(1, 1), stride=(1, 1))
)
(anchor_generator): DefaultAnchorGenerator(
(cell_anchors): BufferList()
)
)
(roi_heads): Res5ROIHeads(
(pooler): ROIPooler(
(level_poolers): ModuleList(
(0): ROIAlign(output_size=(14, 14), spatial_scale=0.0625, sampling_ratio=0, aligned=True)
)
)
(res5): Sequential(
(0): BottleneckBlock(
(shortcut): Conv2d(
1024, 2048, kernel_size=(1, 1), stride=(2, 2), bias=False
(norm): FrozenBatchNorm2d(num_features=2048, eps=1e-05)
)
(conv1): Conv2d(
1024, 512, kernel_size=(1, 1), stride=(2, 2), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv2): Conv2d(
512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv3): Conv2d(
512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=2048, eps=1e-05)
)
)
(1): BottleneckBlock(
(conv1): Conv2d(
2048, 512, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv2): Conv2d(
512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv3): Conv2d(
512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=2048, eps=1e-05)
)
)
(2): BottleneckBlock(
(conv1): Conv2d(
2048, 512, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv2): Conv2d(
512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=512, eps=1e-05)
)
(conv3): Conv2d(
512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False
(norm): FrozenBatchNorm2d(num_features=2048, eps=1e-05)
)
)
)
和FasterRCNN一样的主体结构
(box_predictor): FastRCNNOutputLayers(
(cls_score): Linear(in_features=2048, out_features=82, bias=True)
(bbox_pred): Linear(in_features=2048, out_features=324, bias=True)
(hingeloss): HingeEmbeddingLoss()
)
)
)
实验
增量学习不同阶段的数据集
作者将Pascal VOC和MS-COCO数据集分成4份进行增量学习,4个阶段每个阶段加入20个类别。
[03/27 11:06:46 d2.data.build]: new instances in T1:
| category | #instances | category | #instances | category | #instances |
|---|---|---|---|---|---|
| aeroplane | 361 | bicycle | 700 | bird | 800 |
| boat | 607 | bottle | 2339 | bus | 429 |
| car | 3463 | cat | 522 | chair | 3996 |
| cow | 392 | diningtable | 1477 | dog | 697 |
| horse | 455 | motorbike | 587 | person | 18378 |
| pottedplant | 1043 | sheep | 387 | sofa | 686 |
| train | 385 | tvmonitor | 683 | ||
| [03/27 11:06:46 d2.data.build]: new instances in T2: | |||||
| category | #instances | category | #instances | category | #instances |
| :-------------: | :------------- | :-------------: | :------------- | :----------: | :------------- |
| truck | 474 | ||||
| traffic light | 729 | fire hydrant | 108 | stop sign | 77 |
| parking meter | 63 | bench | 631 | elephant | 259 |
| bear | 73 | zebra | 270 | giraffe | 234 |
| backpack | 560 | umbrella | 516 | handbag | 772 |
| tie | 367 | suitcase | 358 | microwave | 107 |
| oven | 295 | toaster | 17 | sink | 428 |
| refrigerator | 214 | frisbee | skis | ||
| [03/27 11:06:46 d2.data.build]: new instances in T3: | |||||
| category | #instances | category | #instances | category | #instances |
| :-------------: | :------------- | :-------------: | :------------- | :----------: | :------------- |
| frisbee | 138 | skis | 315 | ||
| snowboard | 83 | sports ball | 321 | kite | 474 |
| baseball bat | 195 | baseball gl… | 178 | skateboard | 233 |
| surfboard | 309 | tennis racket | 266 | banana | 586 |
| apple | 394 | sandwich | 335 | orange | 484 |
| broccoli | 541 | carrot | 717 | hot dog | 210 |
| pizza | 518 | donut | 520 | cake | 652 |
[03/27 11:06:46 d2.data.build]: new instances in T4:
| category | #instances | category | #instances | category | #instances |
|---|---|---|---|---|---|
| bed | 189 | toilet | 256 | laptop | 291 |
| mouse | 121 | remote | 330 | keyboard | 176 |
| cell phone | 382 | book | 1507 | clock | 356 |
| vase | 380 | scissors | 46 | teddy bear | 248 |
| hair drier | 17 | toothbrush | 88 | wine glass | 558 |
| cup | 1586 | fork | 407 | knife | 681 |
| spoon | 455 | bowl | 1225 |
实验结果
指标
- Wilderness Impact(WI) metric衡量未知对象很容易被混淆为已知对象的情况,如下式所示。其中 P K P_{\mathcal{K}} PK指的是检测已知类别时的精度,而 P K ∪ U P_{\mathcal{K} \cup \mathcal{U}} PK∪U是检测已知和未知类别时的精度。最理想的情况应该是0,即未知类别全部检测正确。
Wilderness Impact ( W I ) = P K P K ∪ U − 1 \text { Wilderness Impact }(W I)=\frac{P_{\mathcal{K}}}{P_{\mathcal{K} \cup \mathcal{U}}}-1 Wilderness Impact (WI)=PK∪UPK−1
- OPEN-SET ERROR(A-OSE)[43]报告被错误分类为任何已知类别的未知对象的数量计数。
- 为了量化模型在存在新的标记类的情况下的增量学习能力,作者测量了IOU阈值为0.5时的平均平均精度(mAP)
表格
还有一些和其他Open set或者增量学习的方法作比较的结果不总结了。