哈夫曼编码(构建哈夫曼树)
目录
1.哈夫曼树
(1)相关概念
(2)定义
(3)哈夫曼算法
2.哈夫曼编码
(1)相关概念
(2)定义
(3)代码实现
3.完整代码
4.测试输出
1.哈夫曼树
(1)相关概念
- 叶子结点的权值:对叶子结点赋予的一个有意义的数值量(往往体现了访问的频率)
- 二叉树的带权路径长度:设二叉树具有n个带权值的叶子结点,从根结点到各个叶子结点的路径长度与相应叶子结点权值的乘积之和(所有的叶子加起来)
(2)定义
哈夫曼树:给定一组具有确定权值的叶子结点,带权路径长度最小的二叉树
特点:
1,权值越大的叶子结点越靠近根结点,而权值越小的叶子结点越远离根结点
2,只有度为0(叶子结点)和度为2(分支结点)的结点,不存在度为1的结点
(3)哈夫曼算法
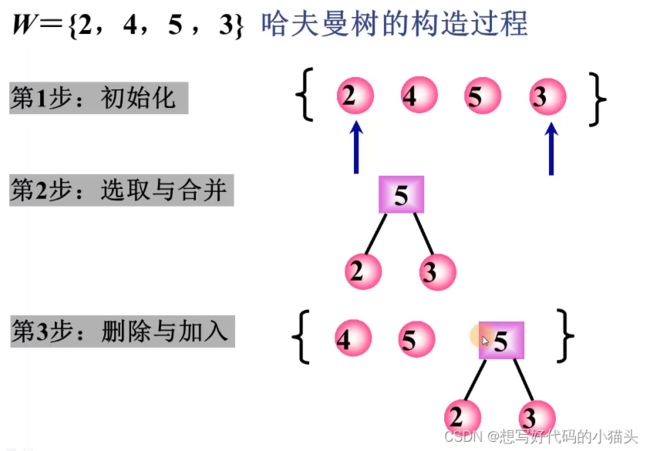
1.基本步骤:
(1)初始化:由给定的n个权值构造n棵只有一个结点的二叉树,构成集合F
(2)选取与合并:在上述结点二叉树集合F中,选取权值最小的两棵树,分别作为左,右子树构建一棵新的二叉树,其权值为左右子树权值之和
(3)删除与加入:在集合F中删除作为左右子树的两棵二叉树,并将新二叉树加入F
(4)重复:(2)(3),直至集合F中只剩下一棵二叉树时,即为哈夫曼树
基本步骤实现如下图: (图片来自懒猫老师《数据结构》相关课程笔记)
2.存储结构
设置一个数组huffTree[2n-1]保存哈夫曼树中各点的信息,数组元素的结点结构如下:
typedef struct element {
int weight;//权值域,保存结点的权值
int lchild, rchild, parent;
//指针域,分别保存结点的左孩子,右孩子和双亲在数组中的下标
} element;为什么存储数组的元素个数为2n-1呢?
这里要引入二叉树的性质,推导过程如下:
3.代码实现
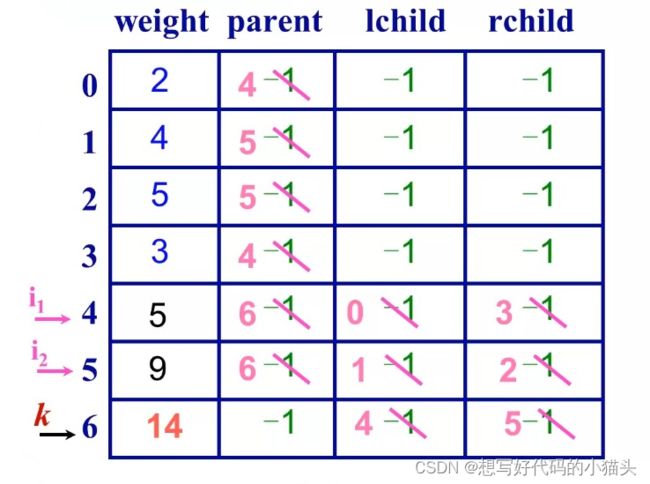
过程图解:
每一次进行合并后,将新二叉树加入数组,修改结点的双亲和左右孩子的下标,构建起结点之间的链接关系;并更新合并后结点的权值
i1 :最小权值结点的下标
i2 :次小权值结点的下标
k :合并后的新结点下标
代码实现:
- void HuffmanTree(element *huffTree, int *w, int n)
参数分别为,哈曼夫树的数组,存放权值的数组,最初的结点个数(也是权值个数)
- select(element *huffTree, int k, int *i1, int *i2)
参数分别为,哈曼夫树的数组,合并后的新结点下标,最小权值结点下标,次小权值结点下标
void HuffmanTree(element *huffTree, int *w, int n) {
int i1, i2;
for (int i = 0; i < 2 * n - 1; i++) { //初始化项目结点
huffTree[i].parent = -1;
huffTree[i].lchild = -1;
huffTree[i].rchild = -1;
}
//初始化前n个结点的权值
for (int i = 0; i < n; i++) {
huffTree[i].weight = w[i];
}
for (int k = n; k < 2 * n - 1; k++) { //构建哈夫曼树
select(huffTree, k, &i1, &i2);
printf("最小下标:%d,次小下标;%d\n", i1, i2);
huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight;//权值相加
huffTree[i1].parent = k;//将k下标赋给即将合并的结点的双亲
huffTree[i2].parent = k;
huffTree[k].lchild = i1;//将合并的两个结点下标赋为k的左右孩子
huffTree[k].rchild = i2;
}
}
void select(element *huffTree, int k, int *i1, int *i2) { //寻找parent为-1的权值最小和次小的两个结点
int index = 0, count = 0, temp;
int arr[k];
for (int i = 0; i < k; i++) {
if (huffTree[i].parent == -1)
arr[count++] = i; //将所有叶子结点的下标保存到arr中
}
for (int i = 0; i < count; i++) {//冒泡排序
for (int j = 0; j < count - i - 1; j++) {
if (huffTree[arr[j]].weight > huffTree[arr[j + 1]].weight) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
*i1 = arr[0];
*i2 = arr[1];
}(最下面有相关的测试完整代码)
2.哈夫曼编码
(1)相关概念
编码:给每一个对象标记一个二进制位串来表示一组对象
前缀编码:一组编码中任一编码都不是其它任何一个编码的前缀(前缀编码保证了在解码时不会有多种可能)
(2)定义
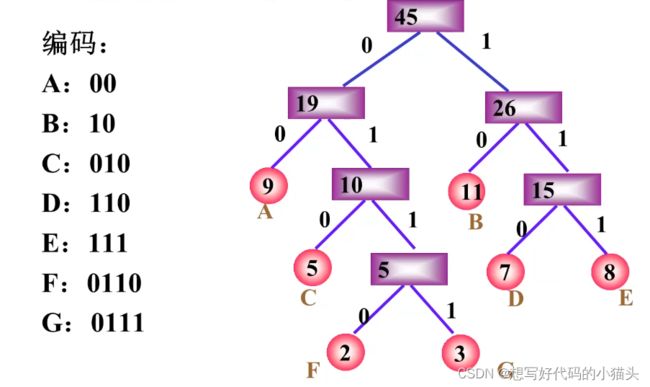
哈夫曼编码就是在哈夫曼树的基础上,从叶子结点开始向上遍历,左孩子记录码为0;右孩子记录码为1。
哈夫曼编码:
(3)代码实现
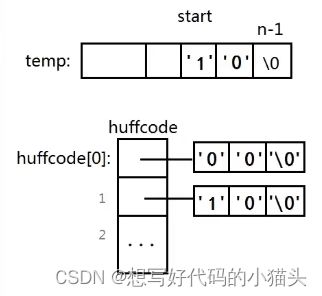
每次循环生成一个权值对应的哈夫曼编码,并从尾部开始存入temp数组中,再赋值给huffCode[n]数组
void huffmanCoding(element *huffTree, char **huffCode, int n) {
char temp[n];//储存临时产生的编码串,n是结点的个数
temp[n - 1] = '\0';
int start, pos, parent;
for (int i = 0; i < n; i++) { //遍历哈夫曼树数组,生成哈夫曼编码
start = n - 1;
pos = i; //pos记录正在处理的当前位置
parent = huffTree[i].parent; //找到父结点
while (parent != -1) { //还能向上寻找根结点
if (huffTree[parent].lchild == pos) //判断当前是左孩子还是右孩子
temp[--start] = '0';
else
temp[--start] = '1';
pos = parent; //当前位置移动到父结点位置
parent = huffTree[parent].parent; //更新父结点
}
huffCode[i] = (char *)malloc(sizeof(char) * (n - start)); //建立哈夫曼编码储存空间
strcpy(huffCode[i], &temp[start]); //将临时储存的哈夫曼编码赋值给对应的空间
}
}
3.完整代码
#include
#include
#include
//输入:
//4
//2 4 5 3
//或者
//7
//9 11 5 7 8 2 3
typedef struct element {
int weight;//权值域,保存结点的权值
int lchild, rchild, parent;
//指针域,分别保存结点的左孩子,右孩子和双亲在数组中的下标
} element;
main() {
int n;
printf("请输入结点个数:");
scanf("%d", &n);
int w[n];
printf("请输入%d个权值:", n);//由权值构建哈夫曼树,可以求出一组哈夫曼编码
for (int i = 0; i < n; i++)
scanf("%d", &w[i]);
element huffTree[2 * n - 1];
HuffmanTree(huffTree, w, n);
printf("该哈夫曼树的带权路径长度:%d\n", huffLength(huffTree, n));
printf("打印构建好的哈夫曼树数组的内容:\n");
printhuffTree(huffTree, n);
char *huffCode[n];
huffmanCoding(huffTree, huffCode, n);
printf("打印生成的哈夫曼编码:");
printf("\n");
printhuffCode(huffCode, n, 1);
printf("完整形式:");
printhuffCode(huffCode, n, 2);
freehuffCode(huffCode, n);
}
void HuffmanTree(element *huffTree, int *w, int n) {
int i1, i2;
for (int i = 0; i < 2 * n - 1; i++) { //初始化项目结点
huffTree[i].parent = -1;
huffTree[i].lchild = -1;
huffTree[i].rchild = -1;
}
//初始化前n个结点的权值
for (int i = 0; i < n; i++) {
huffTree[i].weight = w[i];
}
for (int k = n; k < 2 * n - 1; k++) { //构建哈夫曼树
select(huffTree, k, &i1, &i2);
printf("最小下标:%d,次小下标;%d\n", i1, i2);
huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight;
huffTree[i1].parent = k;
huffTree[i2].parent = k;
huffTree[k].lchild = i1;
huffTree[k].rchild = i2;
}
}
void select(element *huffTree, int k, int *i1, int *i2) { //寻找parent为-1的权值最小和次小的两个结点
int index = 0, count = 0, temp;
int arr[k];
for (int i = 0; i < k; i++) {
if (huffTree[i].parent == -1)
arr[count++] = i; //将所有叶子结点的下标保存到arr中
}
for (int i = 0; i < count; i++) {//冒泡排序
for (int j = 0; j < count - i - 1; j++) {
if (huffTree[arr[j]].weight > huffTree[arr[j + 1]].weight) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
*i1 = arr[0];
*i2 = arr[1];
}
void printhuffTree(element *huffTree, int n) {
printf("weight parent lchild rchild\n");
for (int i = 0; i < 2 * n - 1; i++) {
printf("%3d%8d%8d%8d\n", huffTree[i].weight, huffTree[i].parent, huffTree[i].lchild, huffTree[i].rchild);
}
}
void huffmanCoding(element *huffTree, char **huffCode, int n) {
char temp[n];//储存临时产生的编码串,n是结点的个数
temp[n - 1] = '\0';
int start, pos, parent;
for (int i = 0; i < n; i++) { //遍历哈夫曼树数组,生成哈夫曼编码
start = n - 1;
pos = i; //pos记录正在处理的当前位置
parent = huffTree[i].parent; //找到父结点
while (parent != -1) { //还能向上寻找根结点
if (huffTree[parent].lchild == pos) //判断当前是左孩子还是右孩子
temp[--start] = '0';
else
temp[--start] = '1';
pos = parent; //当前位置移动到父结点位置
parent = huffTree[parent].parent; //更新父结点
}
huffCode[i] = (char *)malloc(sizeof(char) * (n - start)); //建立哈夫曼编码储存空间
strcpy(huffCode[i], &temp[start]); //将临时储存的哈夫曼编码赋值给对应的空间
}
}
void printhuffCode(char **huffCode, int n, int type) {
if (type == 1) {
for (int i = 0; i < n; i++) {
printf("%s\n", huffCode[i]);
}
} else {
for (int i = 0; i < n; i++) {
printf("%s", huffCode[i]);
}
}
}
int huffLength(element *huffTree, int n) { //求带权路径长度
int temp, count = 0, sum = 0;
for (int i = 0; i < n; i++) {
temp = i;
count = 0;
while (huffTree[temp].parent != -1) { //求结点的深度
count++;
temp = huffTree[temp].parent;
}
sum += huffTree[i].weight * count;
}
return sum;
}
void freehuffCode(char **huffCode, int n) {
for (int i = 0; i < n; i++) {
free(huffCode[i]);
}
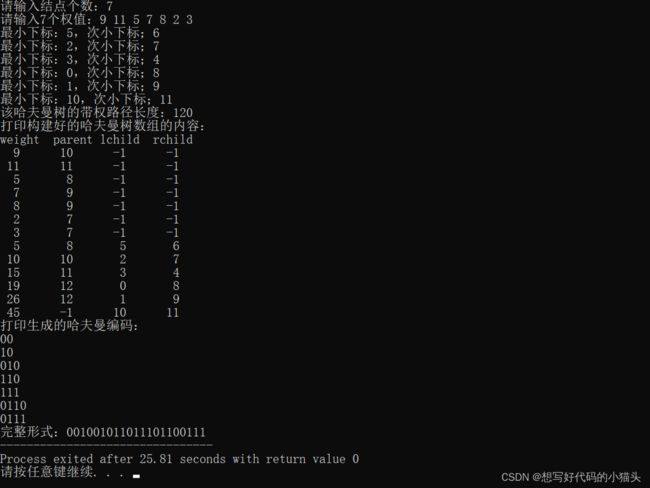
} 4.测试输出
初学小白,有错误欢迎指正喔!X