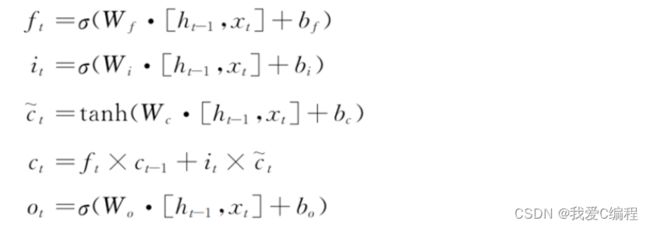m基于HMM和博弈模型的LSTM互联网情感词性分类识别matlab仿真

目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

        传统的情感分析研究大多立足于解决主观性文本的情感分类问题， 面向复杂交互式文本的情感演化分析却力所不逮． 本文以天涯论坛短文本中文在线评论为研究对象， 首先提出一种高效的情感计算框架捕捉在线评论所蕴含的情感倾向； 然后将情感计算和博弈论相结合提出情感演化预测算法， 以混合纳什均衡策略作为交互行为的预测结果； 最后在大规模评论数据集上， 验证了情感计算框架的有效性和情感演化预测算法的准确性.

       在社交网络中，情感传播与信息传播类似。第一，信息传播的研究主体是信息，信息中包含着各种各样的情境，情感传播的研究主体是情感，情感蕴含着丰富多样的类型。第二，情感的传播依赖于信息的传播，所以情感的生命周期同样经历着：潜伏期－爆发期－蔓延期－衰退期。第三，信息传播存在着相互竞争，情感传播存在着相互影响。近年来，网络情感传播研究吸引了信息管理、传播学、心理学、社会学、公共管理等不同领域的学者参与，是一个跨学科研究领域。情感的传播涉及到个体认知、情感、行为多重作用，只有深入理解社会学理论，准确把握情感动力学机制，才能对情感传播进行深入有效的研究。

（1）基于个性特质分类的情感波动度量方法研究。由于个性特质的差异，对于相同事物个体情绪表达的强弱、类型也有所差异。通过分析个体的性格特征，了解个体情感的基线水平，才能准确理解不同情感信息对个体的影响，进而准确分析个体情感对群体情感波动产生的影响。

（2）基于行为预测的情感动力学模型研究。情感产生于个体与其环境交互的过程之中，节点对环境中不同元素的认知与态度的产生变化时，其行为也相应地发生改变。蕴含情感的行为也不断影响了节点，以及节点对环境因素的认知。行为与情感相互作用，行为的演化刺激情感的演化，从而影响了情感传播的方向。行为预测是情感传播预测的基础，可以保证情感传播预测的逻辑性、合理性，再综合考虑个体情感基线的同时，即可提高情感传播预测的精度。

（3）基于博弈论的竞争性情感传播模型研究。在情感传播网络中，个体对于信息传播的决策依赖于利益的博弈，利益的最大化是节点信息与情感扩散的主要动力。与在社交网络信息量爆炸式增长，信息呈现并发式传播，信息间的相互作用同样影响着信息的传播。在相对积极的环境中，信息间的合作关系帮助信息传播，同时也促进情感的扩散。在相对消极的环境中，信息间的竞争关系，抑制了劣势信息的传播，同时也抑制的情感的蔓延。个体决策的博弈以及信息相互的竞争，成就了信息的爆发与情感的蔓延。基于博弈论的竞争的情感传播模型是现实的拓展，研究竞争与博弈共存的传播模型，可以健全情感传播机制，提高情感传播的预测精度。

       长短期记忆网络（LSTM，Long Short-Term Memory）是一种时间循环神经网络，是为了解决一般的RNN（循环神经网络）存在的长期依赖问题而专门设计出来的，所有的RNN都具有一种重复神经网络模块的链式形式。在标准RNN中，这个重复的结构模块只有一个非常简单的结构，例如一个tanh层。

        长短期记忆网络（Long-Short Term Memory,LSTM）论文首次发表于1997年。由于独特的设计结构，LSTM适合于处理和预测时间序列中间隔和延迟非常长的重要事件。LSTM的表现通常比时间递归神经网络及隐马尔科夫模型（HMM）更好，比如用在不分段连续手写识别上。2009年，用LSTM构建的人工神经网络模型赢得过ICDAR手写识别比赛冠军。LSTM还普遍用于自主语音识别，2013年运用TIMIT自然演讲数据库达成17.7%错误率的纪录。作为非线性模型，LSTM可作为复杂的非线性单元用于构造更大型深度神经网络。

       LSTM是一种含有LSTM区块（blocks）或其他的一种类神经网络，文献或其他资料中LSTM区块可能被描述成智能网络单元，因为它可以记忆不定时间长度的数值，区块中有一个gate能够决定input是否重要到能被记住及能不能被输出output。图1底下是四个S函数单元，最左边函数依情况可能成为区块的input，右边三个会经过gate决定input是否能传入区块，左边第二个为input gate，如果这里产出近似于零，将把这里的值挡住，不会进到下一层。左边第三个是forget gate，当这产生值近似于零，将把区块里记住的值忘掉。第四个也就是最右边的input为output gate，他可以决定在区块记忆中的input是否能输出 。LSTM有很多个版本，其中一个重要的版本是GRU（Gated Recurrent Unit），根据谷歌的测试表明，LSTM中最重要的是Forget gate，其次是Input gate，最次是Output gate。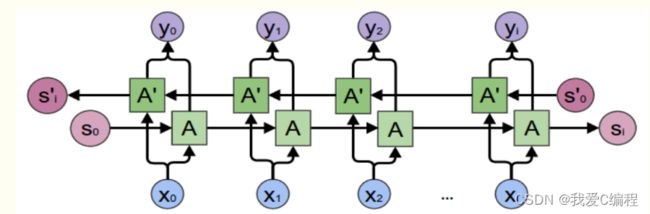

       电力系统负荷预测是指充分考虑历史的系统负荷、经济状况、气象条件和社会事件等因素的影响，对未来一段时间的系统负荷做出预测。负荷预测是电力系统规划与调度的一项重要内容。短期（两周以内）预测是电网内部机组启停、调度和运营计划制定的基础；中期（未来数月）预测可为保障企业生产和社会生活用电，合理安排电网的运营与检修决策提供支持；长期（未来数年）预测可为电网改造、扩建等计划的制定提供参考，以提高电力系统的经济效益和社会效益。复杂多变的气象条件和社会事件等不确定因素都会对电力系统负荷造成一定的影响，使得传统负荷预测模型的应用存在一定的局限性。同时，随着电力系统负荷结构的多元化，也使得模型应用的效果有所降低，因此电力系统负荷预测问题亟待进一步研究。
        电力负荷预测是一种典型的时间序列回归预测任务。电力负荷预测是保证电力供需平衡的基础,并为电网、电源的规划建设以及电网企业、电网使用者的经营决策提供信息和依据。负荷预测分为长期、中期、短期和超短期负荷预测,预测对象包括系统负荷和母线负荷,由电网企业负责组织编制。大用户应根据有关规定,按时报送其主要接装容量和年、月用电量预测及日用电负荷变化过程。

LSTM通过以下公式进行更新权值矩阵和偏置参数等网络信息：

 

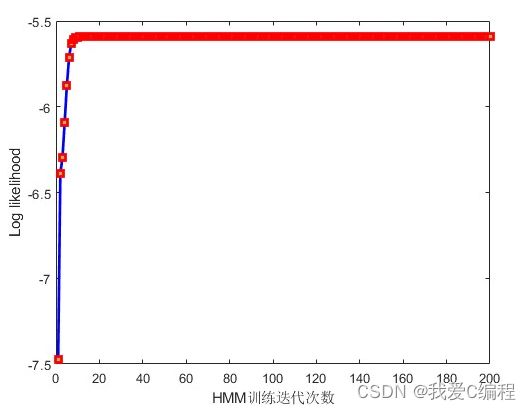
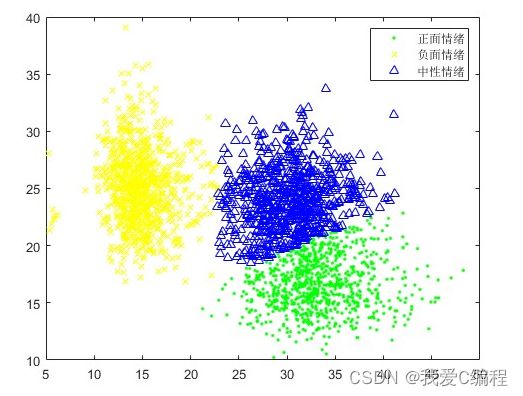
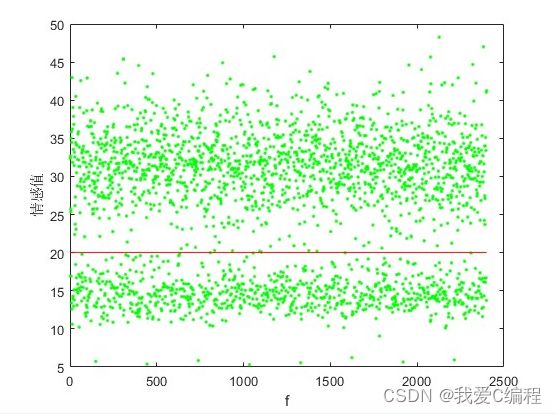
2.仿真效果预览

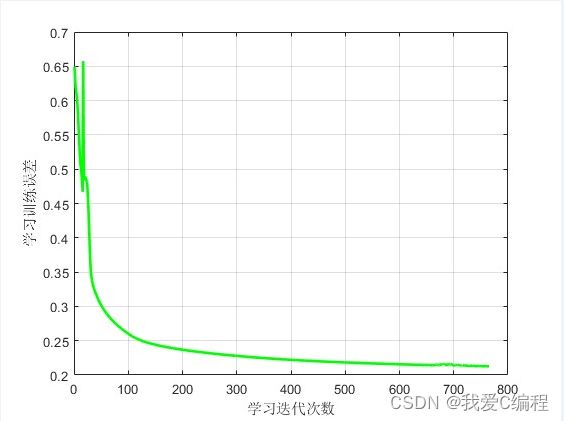
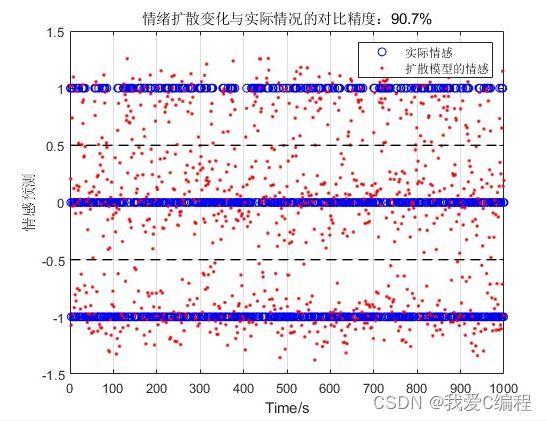
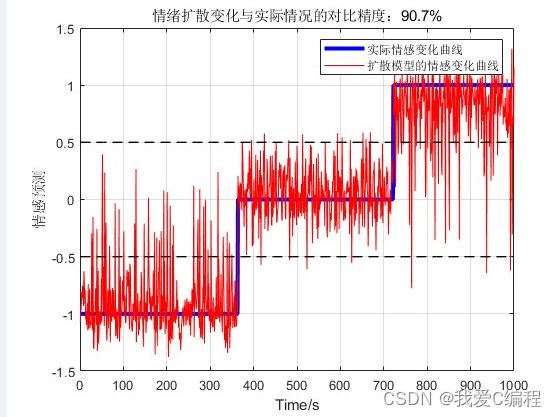
matlab2022a仿真结果如下：

 

 

 

 

 

3.MATLAB核心程序

function [Mu,LL]=func_hmm(X,T,K,Iteration,tol)

p   = length(X(1,:));
N   = length(X(:,1));
N   = N/T;
Cov = diag(diag(cov(X)));
Mu  = randn(K,p)*sqrtm(Cov)+ones(K,1)*mean(X);
Pi  = rand(1,K);
Pi  = Pi/sum(Pi);

P   = rand(K);
P   = rdiv(P,rst_sum(P));

LL  = [];
lik = 0;

alpha = zeros(T,K);
beta  = zeros(T,K);
gamma = zeros(T,K);


B=zeros(T,K);
k1=(2*pi)^(-p/2);

for ij=1:Iteration
    ij
    Gamma   = [];
    Gammasum= zeros(1,K);
    Scale   = zeros(T,1);
    Xi      = zeros(T-1,K*K);
    for n=1:N
        iCov = inv(Cov);
        k2   = k1/sqrt(det(Cov));
        for i=1:T
            for l=1:K
                d       = Mu(l,:)-X((n-1)*T+i,:);
                B(i,l)  = k2*exp(-0.5*d*iCov*d');
            end;
        end;
    
    scale     = zeros(T,1);
    alpha(1,:)= Pi.*B(1,:);
    scale(1)  = sum(alpha(1,:));
    alpha(1,:)= alpha(1,:)/scale(1);
    for i=2:T
        alpha(i,:) = (alpha(i-1,:)*P).*B(i,:);
        scale(i)   = sum(alpha(i,:));
        alpha(i,:) = alpha(i,:)/scale(i);
    end;
    
    beta(T,:) = ones(1,K)/scale(T);
    for i=T-1:-1:1
        beta(i,:) = (beta(i+1,:).*B(i+1,:))*(P')/scale(i); 
    end;
    
    gamma    = (alpha.*beta); 
    gamma    = rdiv(gamma,rst_sum(gamma));
    gammasum = sum(gamma);
    xi       = zeros(T-1,K*K);
    for i=1:T-1
        t       = P.*( alpha(i,:)' * (beta(i+1,:).*B(i+1,:)));
        xi(i,:) = t(:)'/sum(t(:));
    end;
    
    Scale    = Scale+log(scale);
    Gamma    = [Gamma; gamma];
    Gammasum = Gammasum+gammasum;
    Xi       = Xi+xi;
  end;
  Mu =zeros(K,p);
  Mu = Gamma'*X;
  Mu = rdiv(Mu,Gammasum');
  sxi= rst_sum(Xi')';
  sxi= reshape(sxi,K,K);
  P  = rdiv(sxi,rst_sum(sxi));
 
  Pi = zeros(1,K);
  for i=1:N
      Pi=Pi+Gamma((i-1)*T+1,:);
  end
  Pi=Pi/N;
  Cov=zeros(p,p);
  for l=1:K
      d=(X-ones(T*N,1)*Mu(l,:));
      Cov=Cov+rprod(d,Gamma(:,l))'*d;
  end;
  Cov=Cov/(sum(Gammasum));
  
  oldlik = lik;
  lik    = sum(Scale);
  LL     = [LL lik/T];
 
end
end


function Z=rst_sum(X)

Z=zeros(size(X(:,1)));

for i=1:length(X(1,:))
  Z=Z+X(:,i);
end

end


function Z=rdiv(X,Y)
 

Z=zeros(size(X));

for i=1:length(X(1,:))
    Z(:,i)=X(:,i)./Y;
end

end


function Z=rprod(X,Y)

[n m]=size(X);
 

Z=X.*(Y*ones(1,m));
end
05_101_m

4.完整MATLAB

V