项目笔记（一）：实验——用神经网络实现midi音乐旋律音轨的确定

零、写在前面

计划要用seq2seq模型做一个交响乐编曲程序，encoder network的输入是一个乐句旋律，decoder network的目标target是这个乐句完整的管弦配乐版本。本文记录的实验的目的是自动提取出midi乐句的旋律音轨。

一、原理

参考这篇文献中的方法：提取出这个乐句中各个音轨（乐器）的以下特征：

1. 平均力度
2. 所有音符累加总时值
3. 时值类型
4. 最高音与最低音之间的音程
5. 第二高音与第二低音之间的音程

每个音轨的五个特征叠在一起，作为一个乐句的神经网络输入。
对应于主旋律的音轨的one-hot向量作为神经网络的目标输出。

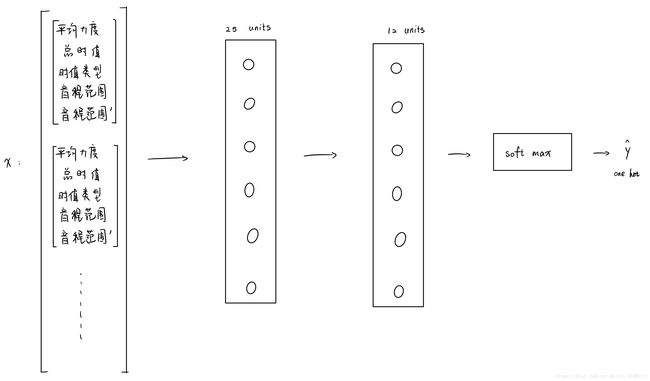
之前文献中，使用了其他的特征作为输入，但那些特征并不十分合理。

二、技术细节

1.midi_to_features.py

这个文件用于提取出一个乐句各个音轨的5个特征值，用了python的pretty_midi包作为处理midi文件的工具。

import pretty_midi

def get_avg_velocity(instrument):
    # 平均力度
    velocity = 0
    for note in instrument.notes:
        velocity += note.velocity
    velocity /= len(instrument.notes)
    return velocity

def get_sum_duration(instrument):
    # 所有音符累加总时值
    duration = 0
    for note in instrument.notes:
        duration += note.end - note.start
    return duration

def get_types_of_duration(instrument):
    # 时值类型
    duration = []
    for note in instrument.notes:
        duration.append(note.end - note.start)
    types = len(set(duration))
    return types

def get_pitch_range(instrument):
    # 最高音与最低音之间的音程
    pitch = []
    for note in instrument.notes:
        pitch.append( note.pitch )
    sorted_pitch = sorted( set(pitch) )

    range = sorted_pitch[-1] - sorted_pitch[0]
    return range

def get_second_pitch_range(instrument):
    # 第二高音与第二低音之间的音程
    pitch = []
    for note in instrument.notes:
        pitch.append( note.pitch )
    sorted_pitch = sorted( set(pitch) )

    range = sorted_pitch[-2] - sorted_pitch[1]
    return range

上面的代码中五个函数对应于提取一个乐句中某一音轨（乐器）的五个特征值。
我们接下来将每一个音轨（乐器）的这五个值，压缩到到一个向量中。

def get_train_example(midi_file):
    pm = pretty_midi.PrettyMIDI( midi_file=midi_file )

    train_example = []

    for instrument in pm.instruments:
        train_example.append(get_avg_velocity(instrument))
        train_example.append(get_sum_duration(instrument))
        train_example.append(get_types_of_duration(instrument))
        train_example.append(get_pitch_range(instrument))
        train_example.append(get_second_pitch_range(instrument))

    return train_example

接下来还要写函数来遍历数据集，提取出各个midi乐句的（一个乐句一个midi文件）特征值。将他们叠在一起，作为训练集的输入。

def get_X_train():
    X_train = [[]]
    for i in range(13): # 一共切取了14个midi片段，其中13个作为训练样本
        midi_file = 'data/x'+str(i+1)+'.mid'
        train_example = get_train_example(midi_file)
        if i==0:
            X_train[0]=train_example
        else:
            X_train.append(train_example)
    return X_train

类似地，再写测试集：

def get_X_test():
    X_test = [[]]

    midi_file = 'data/x14.mid'
    train_example = get_train_example(midi_file)
    X_test[0]=train_example
    return X_test

2. features_to_melody.py

这个文件里用tensorflow构建一个二层神经网络，用matplotlib绘图。我们使用钢琴曲作为数据集，左右手各一个音轨，每个音轨5个特征值，所以一个乐句共有10个特征值。对应的y值显然也只有两种可能。

from midi_to_features import *
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

n_x, n_y = 10, 2

接下来我们制作训练集和测试集的输入和输出，我使用的数据中都是旋律再右手的，所以所有的输出都相同。

# get training data
X_train = get_X_train()
Y_example = [1, 0]
Y_train = [[]]
for i in range (13):
    if i == 0:
        Y_train[0] = Y_example
    else:
        Y_train.append( Y_example )

    #行列互换，使其符合tensorflow的输入格式
X_train = list(map(list, zip(*X_train)))
Y_train = list(map(list, zip(*Y_train)))
print("X_train:", X_train)
print("Y_train:", Y_train)

# get testing data
X_test = get_X_test()
X_test = list(map(list, zip(*X_test)))
Y_test = [[1],[0]]
print("X_test:", X_test)
print("Y_test:", Y_test)

接下来是构建神经网络的准备工作：创建placeholder和初始化参数（用xavier来初始化所有w，用全零初始化b）。

# Create placeholders
def create_placeholders(n_x, n_y):
    X = tf.placeholder(tf.float32, shape=[n_x, None])
    Y = tf.placeholder(tf.float32, shape=[n_y, None])
    return X, Y

# Initialize the parameters
def initialize_parameters():

    W1 = tf.get_variable("W1", [25, n_x], initializer=tf.contrib.layers.xavier_initializer())
    b1 = tf.get_variable("b1", [25, 1], initializer=tf.zeros_initializer())
    W2 = tf.get_variable("W2", [12, 25], initializer=tf.contrib.layers.xavier_initializer())
    b2 = tf.get_variable("b2", [12, 1], initializer=tf.zeros_initializer())
    W3 = tf.get_variable("W3", [n_y, 12], initializer=tf.contrib.layers.xavier_initializer())
    b3 = tf.get_variable("b3", [n_y, 1], initializer=tf.zeros_initializer())

    parameters = {"W1": W1,
                      "b1": b1,
                      "W2": W2,
                      "b2": b2,
                      "W3": W3,
                      "b3": b3}

    return parameters

神经网络的正向传播，激活函数使用relu。

# Forward propagation
def forward_propagation(X, parameters):
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    W3 = parameters['W3']
    b3 = parameters['b3']

    Z1 = tf.add(tf.matmul(W1, X), b1)
    A1 = tf.nn.relu(Z1)
    Z2 = tf.add(tf.matmul(W2, A1), b2)
    A2 = tf.nn.relu(Z2)
    Z3 = tf.add(tf.matmul(W3, A2), b3)

    return Z3

使用softmax作为输出层，定义交叉熵损失。

# Compute Cost
def compute_cost(Z3, Y):
    logits = tf.transpose(Z3)
    labels = tf.transpose(Y)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = labels))
    return cost

现在我们可以开始构建整个模型了。

# the model
def model(X_train, Y_train, X_test, Y_test,learning_rate = 0.0001, num_epochs = 1000,print_cost = True):

    n_x, n_y, = 10, 2, 13
    costs = []
    # 创建placeholder
    X, Y = create_placeholders(n_x, n_y)
    # 初始化参数
    parameters = initialize_parameters()
    # 神经网络前向传播
    Z3 = forward_propagation(X, parameters)
    # 计算损失函数
    cost = compute_cost(Z3, Y)
    #用adam算法最小化损失函数
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
    init = tf.global_variables_initializer()

    # 创建tensorflow的session
    with tf.Session() as sess:
        sess.run(init)
        for epoch in range(num_epochs):
            _, Cost = sess.run([optimizer, cost], feed_dict={X: X_train, Y: Y_train})
            # 打印出cost的变化
            if print_cost == True and epoch % 100 == 0:
                print ("Cost after epoch %i: %f" % (epoch, Cost))
            costs.append(Cost)

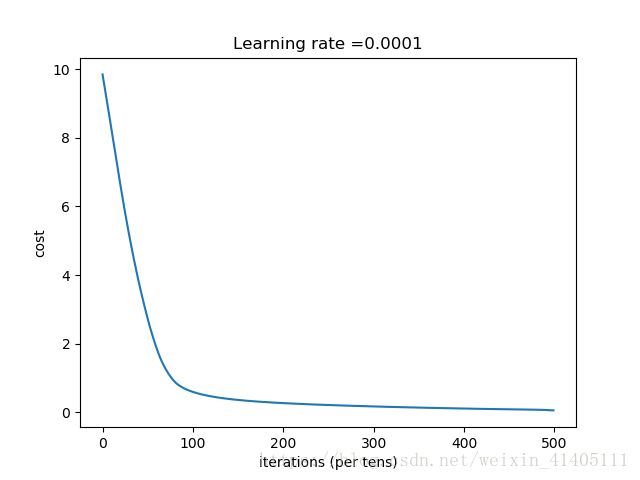
        # 用matplotlib绘制 时间-损失图像
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        parameters = sess.run(parameters)
        print ("Parameters have been trained!")
        correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))

        # 计算准确率
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
        print("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
        print("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))

        return parameters


parameters = model(X_train, Y_train, X_test, Y_test)

3.数据集

这个实验只是为了验证可行性，用了很小很小的数据集（对应无比强烈的过拟合）。我手工提取了莫扎特土耳其进行曲（这是我写过的这首曲子的乐理分析）的一共14旋律材料（14个乐句）。13个作为训练集，最后一个作为测试集。他们可以在这里下载。

我使用的是降b小调的版本，但乐句整体的移调不会影响输出，所以，never mind。

三、结论

Cost after epoch 0: 9.850606
Cost after epoch 100: 0.593675
Cost after epoch 200: 0.267264
Cost after epoch 300: 0.170038
Cost after epoch 400: 0.108876
Parameters have been trained!
Train Accuracy: 1.0
Test Accuracy: 1.0

我们看到，神经网络对于训练集拟合地很好，正确率100%（其实是过拟合），测试样本Test Accuracy: 1.0，即算法正确地分类了测试样本。

这说明，用神经网络实现midi音乐旋律音轨的确定，这一方法是可行的。