【机器学习之支持向量机SVM】
文章目录
- 前言
- 一、思路切入点(带着这几个问题去了解SVM)
- 二、初步认识SVM
-
- 1.svm是什么?能做什么?
-
- ①.什么情况下我们会使用SVM
- ②应用场景总结
- 2.线性可分和不可分问题
-
- ①低维空间与高维空间
- ②什么是最优分类面(超平面)
- ③线性可分和线性不可分
- ④用数学方式解释SVM
- ⑤软间隔与硬间隔
- ⑥问题总结
- 3.LR(逻辑回归)和SVM
-
- ①LR和SVM的联系与区别
- ②什么时候用SVM,什么时候用LR(逻辑回归)?
- 4.线性分类器与非线性分类器的区别以及优劣
- 三、总结
前言
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容支持向量机SVM。
一、思路切入点(带着这几个问题去了解SVM)
① 线性可分、线性不可分如何优化?
② 什么是对偶问题?
③ 核函数的概念、种类和作用是什么?
④ SVM的概念、核心原理以及应用场景有哪些?
⑤ 如何找最优超平面,最大间隔距离,什么叫间隔最大化?
二、初步认识SVM
SVM代码部分可参考:
https://blog.csdn.net/qq_23534759/article/details/79057808?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522165116482916781435477065%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=165116482916781435477065&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allfirst_rank_ecpm_v1~rank_v31_ecpm-4-79057808.142v9pc_search_result_cache,157v4control&utm_term=svm%E4%BB%A3%E7%A0%81python&spm=1018.2226.3001.4187
1.svm是什么?能做什么?
在以前的逻辑回归中,我们是通过sigmoid来分类,但是有很多点在0.5附近,容易出错(离分类线近),所以就引出了一个SVM的思想。
比如举个例子,现在有两色球,我们如何将两色球区分出来,它的一个应用场景,能解决啥内容,通俗点讲SVM其实就是一个分类算法(能做二分类,也能做多分类),它在深度学习没有出来之前,在传统的机器学习的算法里,是非常强大的,独步江湖,它里边有很多的数学原理在里边,很牛的!

①.什么情况下我们会使用SVM
(比如在深度学习中,可以通过textCNN、textRNN做标注去做分类任务,也可以用Bert去做文本分类)相比深度学习,我们什么情况下用SVM做文本分类?什么时候用深度学习呢?
首先不管是SVM还是深度学习的算法,它都是有监督的,都需要我们去做数据标注,我们如何去选择呢?我们为什么去选择SVM呢?它的优势是因为数据量相对比较少的情况下,用SVM效果是不错的,反观深度学习,如果数据量少的话它其实还没有发挥到作用,数据太少,有些特征就没有学习到。
深度学习的强项是,它不需要做特征工程,但是需要做数据标注,而且数据量越大越好,就跟小孩子一样,你教他东西越多,他学到的东西就越多,他就越强,这就是深度学习的强项,数据越多,学习程度就越深,学习到的特征就越多,然后应用表现出来的效果的就越好。
②应用场景总结
总结一下,什么时候用SVM?首先它可以做二分类,也可以做多分类,数据量相对比较少的情况下,可以用SVM。
2.线性可分和不可分问题
①低维空间与高维空间
还是那个例子,两色球在我们二维平面的低维度空间下,可以通过一条线将两色球区分开,
如果他上升为高维空间呢?它就只能通过一个面来把两色球区分开来。在低维空间中的双色球,始终有一条线把它们区分开来,可能会有点难看,但是上升到高维空间,比如说3维空间中,我们又引出另一个概念就是超平面,同样将两色球分开,怎样找出这个超平面,就是SVM最核心的要解决的。也就是说SVM的核心原理就是将一个输入空间映射到一个新的空间,把我们的分类问题转化成找到一个求解最优的分类面(超平面)的问题。
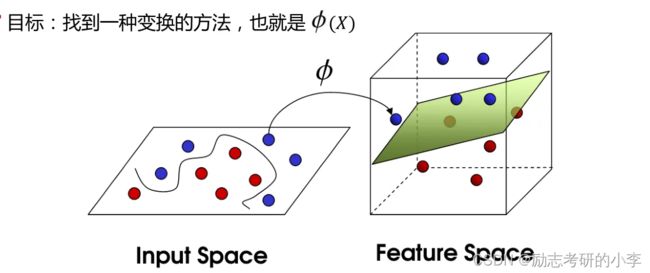
②什么是最优分类面(超平面)
什么是最优分类面(超平面)呢?这里又引出一个概念,就是要找到最大间隔距离,意思就是距离分类面最近的点(球)距离越远越好,基本模型定义为特征空间上的间隔最大的线性分类器,它的一个学习策略就是间隔最大化。
那么如何从低维的空间找到那条线转化成高维的空间里找那个面?传统要用数学去解决的话怎么解决?一条线好处理,一条面怎么办?这就需要引入核函数,核函数就是用来简化计算的复杂度,这就是引入它的一个目的。
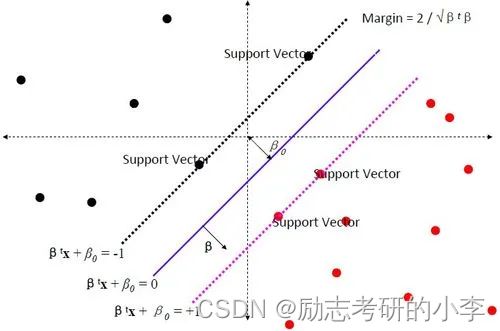
③线性可分和线性不可分
这里有两个概念,就是线性可分和非线性可分。在线性可分情况下,如何去优化SVM呢?我们选择将我们的问题转化成用对偶问题去处理。什么叫对偶问题呢?就是说要解决A问题的这种情况,很难处理,我们选择找一个同A问题同等或几乎类似的B问题,而B问题解决的思路非常简单,反过来解决了B问题,我们就解决了A问题,这就是对偶问题,但这种情况只能是线性可分情况下,才可以对SVM进行优化处理。
但是对于非线性可分的情况下呢,SVM的处理方式就选择一个核函数,它在SVM中的作用就是将数据映射到高维空间,来解决在原始空间中线性不可分的问题。核函数都有哪些呢?比如说有多项式核、高斯核、线性核。

④用数学方式解释SVM
用数学的方式解释SVM的话就是去通过拉格朗日乘数法将多个变量和多个约束问题转化为多个变量的无约束优化问题,使用KKT条件构造数据不等式后,对不等式求对偶,得到它的对偶不等式,然后方便核函数的引入,同时我们就将无约束问题转化成有约束条件的求解问题,最后通过对该不等式求极值,然后我们就可以得到分类类别拉姆达及距离分类线最近的支持向量。
(求偏导–>求出×1,x2–>带入拉格朗日函数–>剩一个入(拉姆达)变量,求偏导–>找到最优x1,×2,可以求出最小的。求解带有优化条件需要拉格朗日乘子法。不是凸优化问题不可以求解,凸优化问题的可以求解)
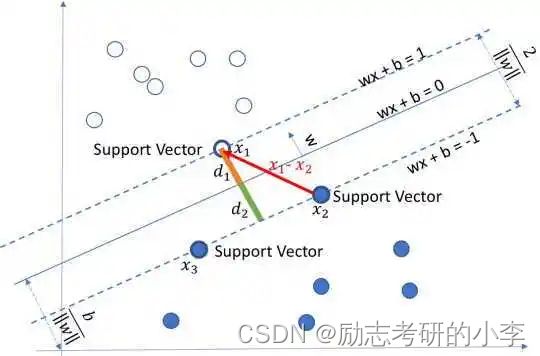
⑤软间隔与硬间隔
软间隔: 允许个别样本分类错误,硬间隔与之相反。
硬间隔: 不允许任何错误的发生,样本点中间不能有其他样本点。
SVM采用的是基于距离的软间隔分类方法。基于个数的软间隔分类方法由于反向传播期间不可导而未被使用。
⑥问题总结
1)是否存在—组参数使SVM训练误差为0? ★★★☆☆
答: 存在
2)训练误差为0的SVM分类器—定存在吗? ★★☆☆☆
答: 一定存在,肯定能找到一组,这也是为什么在传统机器学习独步江湖,那么牛的存在!
3)加入松弛变量的SVM的训练误差可以为0吗? ★★☆☆☆
答∶ 使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由于我们的优化目标改变了,并不再是使训练误差最小。就是说不一定!
4)带核的SVM为什么能分类非线性问题?(核函数的作用是什么? ) ★★★★☆
答:核函数的本质是两个函数的内积,通过核函数将其隐射到高维空间,在高维空间非线性问题转化为线性问题,SVM得到超平面是高维空间的线性分类平面。其分类结果也视为低维空间的非线性分类结果,因而带核的SVM就能分类非线性问题。
5)如何选择核函数? ★★★★☆
① 如果特征的数量大到和样本数量差不多,就选用LR或者线性核的SVM;
② 如果特征的数量小,样本的数量正常,就选用SVM+高斯核函数;(重点)
③ 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。(我们一般用深度学习)
3.LR(逻辑回归)和SVM
代码可参考:
(https://www.csdn.net/tags/OtDaQg5sMjY0NTktYmxvZwO0O0OO0O0O.html)
①LR和SVM的联系与区别
1)相同点
① 都是一个分类器。都可以做二分类;
② 都是有监督学习算法;
③ 都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有: KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型;
④ 都可以处理非线性问题。
2)不同点
① LR是参数模型,SVM是非参数模型,linear(线性)和rbf(径向基函数)则是针对数据线性可分和不可分的区别。SVM非参数模型存在线性不可分的情况,要是线性可分的情况运用线性核函数,就更像逻辑回归了;
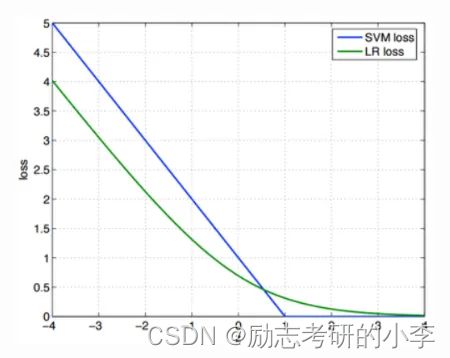
② 它们的损失函数不同,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss(最大间隔损失函数),这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重;
③ LR一般不用核函数,SVM用到核函数;
④ SVM计算复杂,但效果比LR好,适合小数据集;LR计算简单,适合大数据集,可以在线训练;
⑤ logic能做的SVM能做,但可能在准确率上有问题,但是SVM能做的logic有的做不了。
②什么时候用SVM,什么时候用LR(逻辑回归)?
比如说m是样本数,n是特征的数目。
- 如果n相对于m来说很大,就使用logistic回归或者不带核函数的SVM(线性分类);
- 如果n很小,m的数量适中(n=1-1000,m=10-10000),使用带核函数的SVM算法;
- 如果n很小,m很大(n=1-1000,m=50000+),增加更多的特征,然后使用logistic回归或者不带核函数的SVM。
特征比较小,而且数据量不大(适中)就可以用SVM,特征相对于样本来说很大,也就是特征很多数据量比较少那么就用逻辑回归。
4.线性分类器与非线性分类器的区别以及优劣
线性和非线性是针对模型参数和输入特征来讲的;比如输入x,模型y=ax+ax2那么就是非线性模型,如果输入是x和X2则模型是线性的。
- 线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
- 非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
SVM两种都有(看线性核还是高斯核)
三、总结
提示:这里对文章进行总结:
1. svm是一个分类器,作用于数据量相对比较少的情况下。
2. 是一个有监督的判别式模型。
3. 可以处理线性可分及不可分问题。
以上就是今天要讲的内容,本文仅仅简单介绍了svm的使用,而svm提供了大量能使我们快速便捷地处理数据的函数和方法。