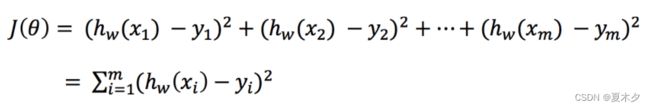机器学习算法（2）—— 线性回归算法

1 线性回归简介

线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

• h代表学习算法的解决方案或函数，也称为假设（hypothesis），h(x)代表预测的值

注意：

• 只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归
• 特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。
• 线性回归当中主要有两种模型，一种是线性关系，另一种是非线性关系

2 线性回归的初步使用

线性回归API

sklearn.linear_model.LinearRegression()

• LinearRegression.coef_：回归系数

'''导入模块'''
from sklearn.linear_model import LinearRegression

'''构造数据集'''
x = [[80, 86],
	 [82, 80],
	 [85, 78],
	 [90, 90],
	 [86, 82],
	 [82, 90],
	 [78, 80],
	 [92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]

'''模型训练'''
# 实例化一个估计器
estimator = LinearRegression()
# 使用fit方法进行训练
estimator.fit(x,y)
# 查看回归系数值
coef = estimator.coef_
print("系数是：\n",coef) # [0.3 0.7]
# 预测值
prediction = estimator.predict([[100, 80]])
print("预测值是：\n",prediction) # [86.]

3 损失函数

为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数

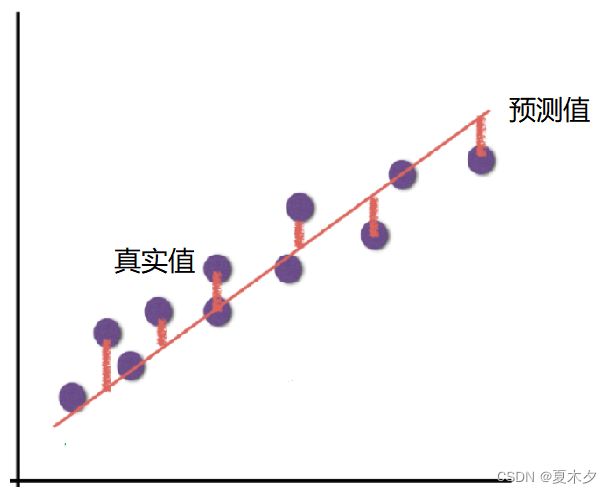
如上图所示，真实结果与我们预测的结果之间存在一定的误差，而这个误差（损失）可以计算出来：

注意：

• yi为第i个训练样本的真实值

• h(xi)为第i个训练样本特征值组合预测函数

• 又称最小二乘法

• 损失函数（Loss Function）度量单样本预测的错误程度，损失函数值越小，模型就越好。

• 代价函数（Cost Function）度量全部样本集的平均误差。

• 目标函数（Object Function）代价函数和正则化函数，最终要优化的函数。

4 优化算法

如何去求模型当中的W，使得损失最小？（目的是找到最小损失对应的W值）

线性回归经常使用的两种优化算法

• 正规方程
• 梯度下降法

4.1 正规方程

1. 什么是正规方程
   

2. 正规矩阵求解

把损失函数转换成矩阵写法：

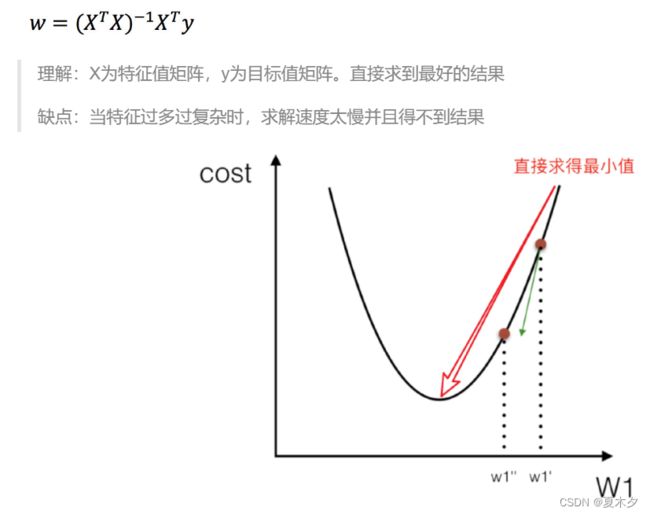
其中y是真实值矩阵，X是特征值矩阵，w是权重矩阵

对其求解关于w（w为自变量）的最小值，导数为零的位置，即为损失的最小值

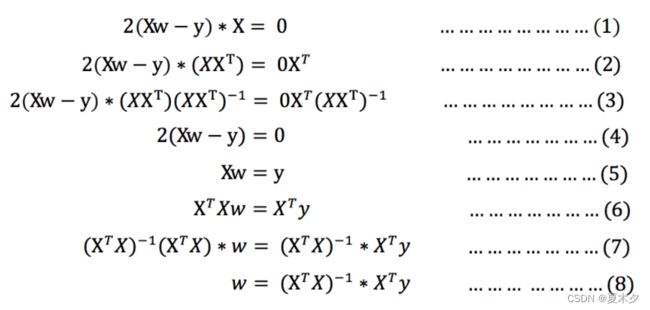
注意：

• 式(1)到式(2)推导过程中,X是一个m行n列的矩阵，并不能保证其有逆矩阵，但是右乘X的转置XT把其变成一个方阵，保证其有逆矩阵。式（5）到式（6）推导过程中，和上类似。（面试官可能让你手推公式）

即正规方程为：

• X为特征值矩阵，y为目标值矩阵。直接求到最好的结果
• 当特征过多过复杂时，求解速度太慢并且得不到结果

4.2 梯度下降

1. 梯度下降

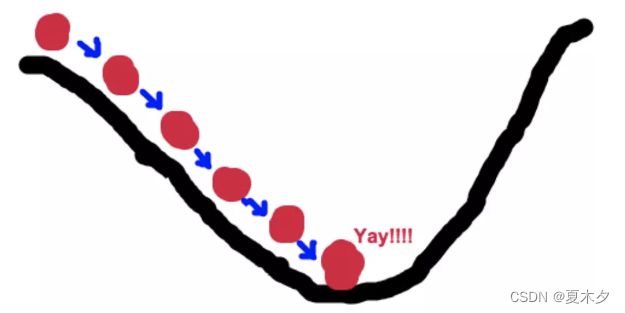
梯度下降法的基本思想可以类比为一个下山的过程。

假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，（同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走）。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

梯度是微积分中一个很重要的概念

• ​ 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率。
• ​ 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向（α为负的原因）一直走，就能走到局部的最低点！

2. 梯度下降公式

梯度下降公式（Gradient Descent）

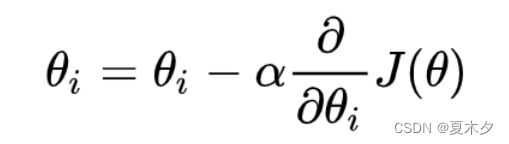
注意：
α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点。

所以有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力

3. 梯度下降举例

（1） 单变量函数的梯度下降

我们假设有一个单变量的函数 :J(θ) = θ²
函数的微分:J’(θ) = 2θ
初始化，起点为： θº = 1
学习率：α = 0.4
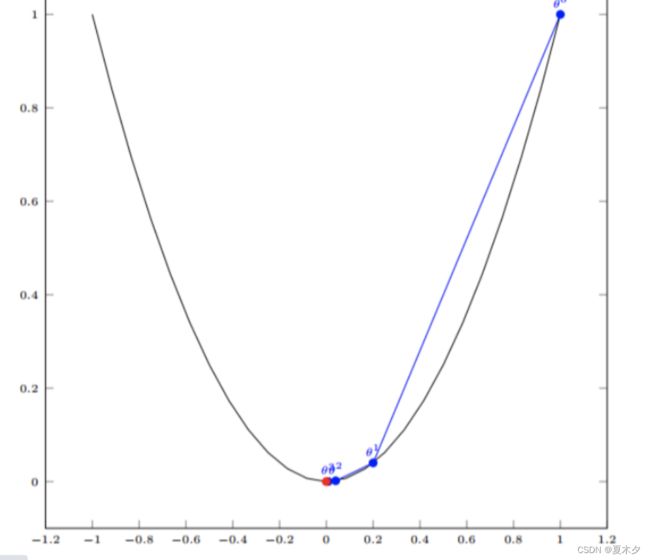
我们开始进行梯度下降的迭代计算过程:

如下图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底

（2）多变量函数的梯度下降

我们假设有一个目标函数 ：:J(θ) = θ₁² + θ₂²
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0，0)点。但是接下 来，我们会从梯度下降算法开始一步步计算到这个最小值! 我们假设初始的起点为: θº = (1, 3)
初始的学习率为:α = 0.1
函数的梯度为:▽:J(θ) =< 2θ₁ ,2θ₂>

进行多次迭代:

我们发现，已经基本靠近函数的最小值点

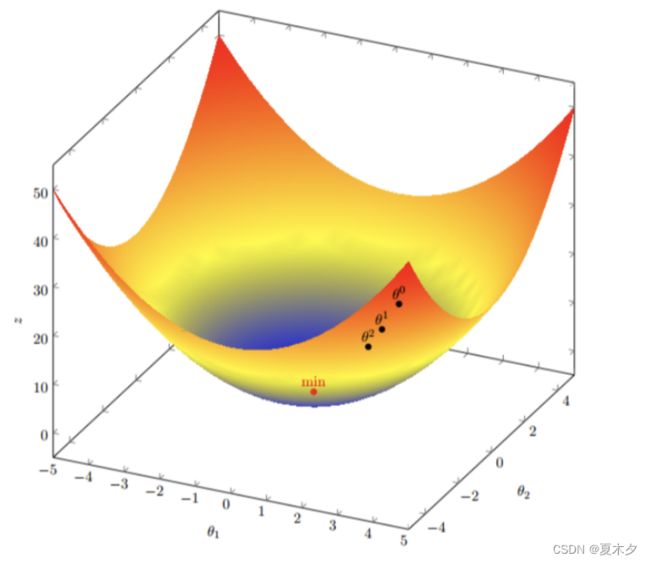
4. 梯度下降算法

常见的梯度下降算法有：

• 全梯度下降算法(Full gradient descent），
• 随机梯度下降算法（Stochastic gradient descent），
• 随机平均梯度下降算法（Stochastic average gradient descent）
• 小批量梯度下降算法（Mini-batch gradient descent）,

它们都是为了正确地调节权重向量，通过为每个权重计算一个梯度，从而更新权值，使目标函数尽可能最小化。其差别在于样本的使用方式不同。

（1）全梯度下降算法（FG）

（2）随机梯度下降算法（SG）

（3）小批量梯度下降算法（mini-bantch）

（4）随机平均梯度下降算法（SAG）

（5）算法比较

以下6幅图反映了模型优化过程中四种梯度算法的性能差异。

结论：

• FG方法由于它每轮更新都要使用全体数据集，故花费的时间成本最多，内存存储最大。
• SAG在训练初期表现不佳，优化速度较慢。这是因为我们常将初始梯度设为0，而SAG每轮梯度更新都结合了上一轮梯度值。
• 综合考虑迭代次数和运行时间，SG表现性能都很好，能在训练初期快速摆脱初始梯度值，快速将平均损失函数降到很低。但要注意，在使用SG方法时要慎重选择步长，否则容易错过最优解。
• mini-batch结合了SG的“胆大”和FG的“心细”，从6幅图像来看，它的表现也正好居于SG和FG二者之间。在目前的机器学习领域，mini-batch是使用最多的梯度下降算法，正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点。

4.3 优化方法比较

1. 梯度下降要设置α并不保证一次能获得最优的α，正规方程不用考虑α。
2. 梯度下降要迭代多次，正规方程不用。（所以，遇到比较简单的情况，可用正规方程）
3. 梯度下降最后总能得到一个最优结果，正规方程不一定。因为正规方程要求X的转置乘X的结果可逆。
4. 当特征数量很多的时候，正规方程计算不方便，不如梯度下降。

算法选择依据：

• 小规模数据：
  • 正规方程：LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：
  • 梯度下降法： SGDRegressor

4.4 线性回归api再介绍

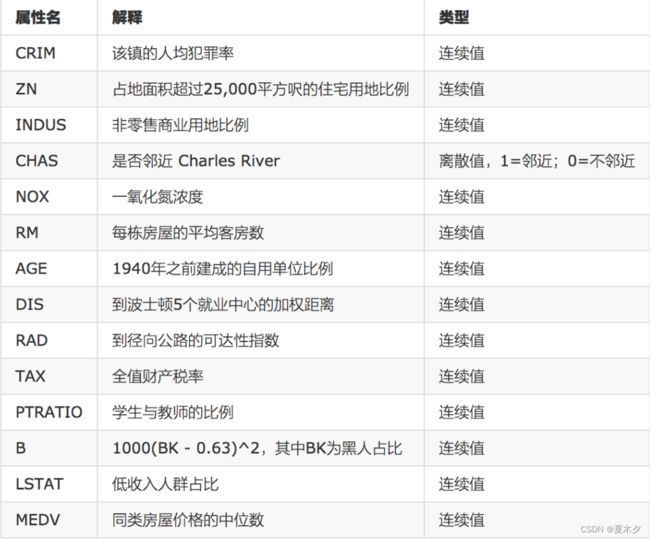
数据集介绍

（1）线性回归:正规方程

sklearn.linear_model.LinearRegression(fit_intercept=True)

• fit_intercept：是否计算偏置
• LinearRegression.coef_：回归系数（y=kx+b中的 k）
• LinearRegression.intercept_：偏置（y=kx+b中的 b）

回归模型评估

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

'''获取数据集'''
data = load_boston()

'''划分数据集'''
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)

'''特征工程：数据标准化'''
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

'''机器学习：线性回归（正规方程）'''
estimator = LinearRegression()
estimator.fit(x_train, y_train)

'''模型评估'''
y_predict = estimator.predict(x_test)
print("预测值为：", y_predict)
print("系数值为：", estimator.coef_)
print("偏置值为：", estimator.intercept_)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：", error)

（2）线性回归:梯度下降法

SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。

sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)

参数：

• loss:损失类型
  • loss=”squared_loss”: 普通最小二乘法
• fit_intercept：是否计算偏置
• learning_rate : 学习率填充， string类型，optional
  • 'constant': eta = eta0 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
  • 'optimal': eta = 1.0 / (alpha * (t + t0)) [default]
  • 'invscaling': eta = eta0 / pow(t, power_t)

属性：

• SGDRegressor.coef_：回归系数
• SGDRegressor.intercept_：偏置

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

'''获取数据集'''
data = load_boston()

'''划分数据集'''
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)

'''特征工程：数据标准化'''
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

'''机器学习-线性回归(特征方程)'''
estimator = SGDRegressor(max_iter=1000)
estimator.fit(x_train, y_train)

'''模型评估'''
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)

'''评价'''
error = mean_squared_error(y_test, y_predict)
print("均方误差为:\n", error)

5 欠拟合与过拟合

5.1 欠拟合

概念：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

原因：学习到数据的特征过少

解决办法：

• 添加其他特征项
• 添加多项式特征

5.2 过拟合

概念：一个假设在训练数据上能够获得更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)

原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点

解决办法：

• 重新清洗数据
• 增大数据的训练量
• 正则化
• 减少特征维度，防止维灾难

正则化


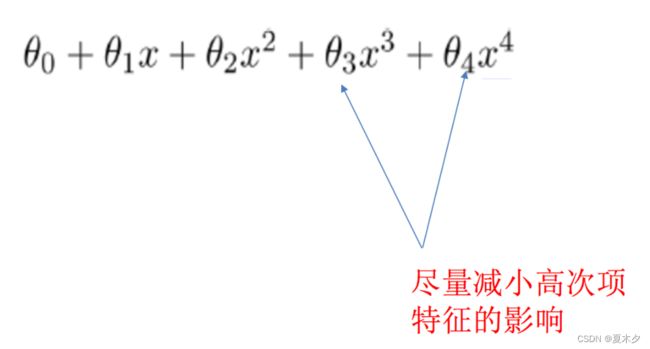
在学习的时候，数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多，所以算法在学习的时候尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化

L1正则化

• 作用：可以使得其中一些W的值直接为0，删除这个特征的影响
• LASSO回归

L2正则化

• 作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
• 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
• Ridge回归

维灾难

随着维度的增加，分类器性能逐步上升，到达某点之后，其性能便逐渐下降。

6 正则化线性模型

6.1 Ridge Regression 岭回归

岭回归是线性回归的正则化版本，即在原来的线性回归的 cost function 中添加正则项：
以达到在拟合数据的同时，使模型权重尽可能小的目的,岭回归代价函数:

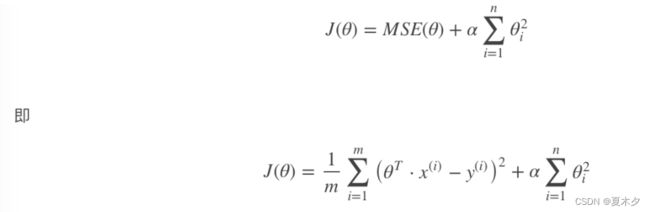
注意：

• α=0时，岭回归退化为线性回归
• 就是把系数添加平方项，然后限制系数值的大小，α值越小，系数值越大，α越大，系数值越小

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)

• 具有l2正则化的线性回归

参数：

• alpha:正则化力度，也叫 λ，λ取值：0~1 或者 1~10（正则化力度越大，权重系数越小，反之，越大）
• solver:会根据数据自动选择优化方法，sag:如果数据集、特征都比较大，选择该随机梯度下降优化
• normalize:数据是否进行标准化，normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据

属性：

• Ridge.coef_:回归权重
• Ridge.intercept_:回归偏置

Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)

• 具有l2正则化的线性回归，可以进行交叉验证
• coef_:回归系数

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge, RidgeCV
from sklearn.metrics import mean_squared_error
import joblib

'''获取数据集'''
data = load_boston()

'''划分数据集'''
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)

'''特征工程：数据标准化'''
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

'''机器学习：岭回归'''
# estimator = Ridge()
estimator = RidgeCV(alphas=(0.1, 1, 10))
estimator.fit(x_train, y_train)

'''模型评估'''
y_predict = estimator.predict(x_test)
print("预测值为：", y_predict)
print("系数值为：", estimator.coef_)
print("偏置值为：", estimator.intercept_)
error = mean_squared_error(y_test, y_predict)
print("均方误差为：", error)

6.2 Lasso 回归

Lasso回归的代价函数 ：
Lasso Regression 的代价函数在 θi=0处不可导，可以在θi=0处用一个次梯度向量(subgradient vector)代替梯度：

注意：

• Lasso Regression 的代价函数在 θi=0处是不可导的
• 倾向于完全消除不重要的权重
• 对系数值进行绝对值处理，由于绝对值在顶点处不可导，所以进行计算的过程中产生很多0，最后得到结果为：稀疏矩阵

6.3 Elastic Net 弹性网络

弹性网络的代价函数 ：

弹性网络在岭回归和Lasso回归中进行了折中，通过 混合比(mix ratio) r 进行控制：

• r=0：弹性网络变为岭回归
• r=1：弹性网络便为Lasso回归

注意：

• 常用：岭回归
• 假设只有少部分特征是有用的：
  • 弹性网络
  • Lasso
  • 一般来说，弹性网络的使用更为广泛。因为在特征维度高于训练样本数，或者特征是强相关的情况下，Lasso回归的表现不太稳定。

6.4 Early stopping

Early Stopping 也是正则化迭代学习的方法之一。
其做法为：在验证错误率达到最小值的时候停止训练。

7 模型的保存与加载

from sklearn.externals import joblib

• 保存：joblib.dump(estimator, 'test.pkl')
• 加载：estimator = joblib.load('test.pkl')

注意：

• 保存文件，后缀名是**.pkl
• 加载模型是需要通过一个变量进行承接