遗传算法(Python) #3 从零开始解决OneMax问题

遗传算法(Python) #3 从零开始解决OneMax问题

1. OneMax问题(OneMax Problem)

OneMax问题是遗传算法的入门问题，其内容是：如何使一段长度固定的二进制字符串所有位置上数字之和最大。

让我们用一个长度为5的二进制字符串为例：

• 10010 -> 和为2
• 00111 -> 和为3
• 11111 -> 和为5(最大值)

对一般人，显而易见，当所有位数都为1时，该字符串的和最大，但在我们用遗传算法解决该问题时，遗传算法本身并没有这样的知识。接下来我们将不依靠任何遗传算法的包，从头开始用遗传算法解决OneMax问题。

2.问题的解决思路

首先，我们得把这个问题转换成一个遗传算法问题，即：我们得定义个体、种群，选择、杂交、突变方法、适应度函数等。假设有一个长度为100的字符串，我们可以做出以下定义：

• 个体：个体即为问题的解，这个问题中个体可以直观的定义为一个长度为100列表（List），列表上每个元素为0或1.
• 种群：种群即所有个体的合集，我们可以把种群定义为所有个体组成的列表。
• 选择：使用锦标赛法(Tournament Selection)
• 杂交：使用单点杂交法(Singe-Point Crossover)
• 突变：使用位翻转突变法(Flip Bit Mutation)
• 适应度函数： 我们的目标是使字符串上所有数字之和最大，适应度函数可以直观的定义为列表中所有数字之和。

若对上述定义不太了解的，可以回看遗传算法系列的第二期。

3.用Python实现遗传算法

以下将分步骤解释每一部分的代码，完整代码在本文的最后可见。

0.准备工作

import random
import matplotlib.pyplot as plt
random.seed(39)

导入所有需要的包：

• random： 用于生成随机数
• matplotlib： 用于画图
• random.seed: 确定种子（即随机状态），这样每次运算我们都能得到同样的结果

1.定义个体和种群

# 1. define individual and population
def CreateIndividual():
    return([random.randint(0,1) for _ in range(100)])

def CreatePopulation(size):
    return([CreateIndividual() for _ in range(size)])

• CreateIndividual：个体即为一个长度为100的列表，每个元素（基因）为0或1。
• CreatePopulation： 种群即多个个体组成的列表。

2.定义选择、杂交、突变方法和适应度函数

1.选择

# 2.1. define select function
def tournament(population,size):
    participants = random.sample(population,size)
    # evaluate function is defined in 3.4
    winner = max(participants,key=lambda ind:evaluate(ind))
    return(winner.copy())

def select(population,size):
    return([tournament(population,size) for _ in range(len(population))])

• tournament：从种群中随机抽取size个个体，从中选取适应度最高的个体。
  • 注意使用.copy以防同一个列表被多次引用。
• select：为了保持种群的大小不变，锦标赛的次数应与种群中个体的数量相同

2.杂交

# 2.2. define mate function
def SinglePointCrossover(ind1,ind2):
    loc = random.randint(0,len(ind1)-1)
    genes1 = ind1[loc:]
    genes2 = ind2[loc:]
    ind1[loc:] = genes2
    ind2[loc:] = genes1
    return([ind1.copy(),ind2.copy()])

def mate(population,probability):
    new_population = []
    for i in range(0,len(population),2):
        ind1 = population[i].copy()
        ind2 = population[i+1].copy()
        if random.random() < probability:
            new_population.extend(SinglePointCrossover(ind1,ind2))
        else:
            new_population.extend([ind1,ind2])
    return(new_population)

• SinglePointCrossover：单点杂交法的实现，两个个体交换随机位置及其后面的基因
• mate：对种群进行杂交，按一定概率每两个相邻的个体进行杂交
  • probability参数：每次生成一个0至1之间的随机数，若随机数小于该概率，则进行杂交，否则对应的两个个体被克隆。

3.突变

# 2.3. define mutate function
def flipOneGene(ind):
    loc = random.randint(0,len(ind)-1)
    ind[loc] = 1 - ind[loc] # 0->1 or 1->0
    return(ind.copy())

def mutate(population,probability):
    new_population = []
    for ind in population:
        if random.random() < probability:
            new_population.append(flipOneGene(ind))
        else:
            new_population.append(ind.copy())
    return(new_population)

• flipOneGene:位翻转突变，个体上的一个随机基因进行突变。
• mutate: 每个个体都以一定概率突变，若不突变，则该个体被克隆。

4.适应度函数

# 2.4. define evaluate function
def evaluate(individual):
    return(sum(individual))

OneMax的适应度函数就是列表中所有数字之和。

5.统计种群数据

# 2.5. define statistical metrics to monitor algorithm performance
def population_score_max(population):
    return(max([evaluate(ind) for ind in population]))

def population_score_mean(population):
    return(sum([evaluate(ind) for ind in population])/len(population))

为了追踪算法的进度和发现算法中可能出现的错误，我们可以统计每次迭代中种群适应度的最大值与均值。

3.运行遗传算法

# 3. Run genetic algorithm
def main(
    POPULATION_SIZE = 100,
    TOURNAMENT_SIZE = 3,
    CROSSOVER_PROB = 0.9,
    MUTATE_PROB = 0.1,
    MAX_GENERATIONS = 100
):
    generation = 0
    population = CreatePopulation(POPULATION_SIZE)
    max_scores = [population_score_max(population)]
    mean_scores = [population_score_mean(population)]
    best_individual = []
    while generation < MAX_GENERATIONS:
        population = select(population,TOURNAMENT_SIZE)
        population = mate(population,CROSSOVER_PROB)
        population = mutate(population,MUTATE_PROB)
        # collect statistics
        max_scores.append(population_score_max(population))
        mean_scores.append(population_score_mean(population))
        best_individual = max(
            best_individual,
            max(population,key=lambda ind: evaluate(ind))
        ).copy()
        generation += 1
    
    print("Best Solution:")
    print(best_individual)
    plt.plot(max_scores, color='red',label="Max Score")
    plt.plot(mean_scores, color='green',label="Mean Score")
    plt.legend()
    plt.xlabel("Generations")
    plt.ylabel("Fitness Score")
    plt.grid()
    plt.show()   

if __name__ == "__main__":
    main()

在运行算法前，我们首先得定义一些参数：

• 种群大小(Population Size):一般而言种群越大，越容易在较小的代数内获得最优解，但代价是每一代的运算量会变大。
• 锦标赛大小（Tournament Size）: 锦标赛的大小一般不要取的太大，否则种群容易因过早地失去多样性而过早收敛。举一个极端例子，当种群大小为100且锦标赛大小也为100时，第一次选择后所有的个体都会变成同一个个体，算法便很难再有改善的空间。
• 杂交概率（Crossover Probability）：杂交的概率应取一个较大的值，比如0.7,0.8,0.9等，具体数值应视具体情况而定。
• 突变概率（Mutate Probability）：突变概率应取一个较小的值，如0.05，0.1，0.2等，若取值太大，则种群的随机性太强，不利于保存适应度高的个体，从而使遗传算法变成完全随机的搜索。
• 最大代数(Max Generation):遗传算法不可能无止尽的运行下去，一般而言，我们都会设置终止条件，这个问题中，我们以最大代数为终止条件，当迭代进行到一定次数时算法终止。

在迭代过程中，每一代里我们都进行选择(select),杂交(mate)，突变(mate)运算，并收集种群的最大和平均适应度数据，用以追踪算法的进度，或发现算法中存在的问题。视问题而定，我们还可以记录下每代中适应度最高的个体(best individual)，以防止其因杂交和突变而消失。

最后，我们观察最优解与种群的数据。

4.算法结果

我们成功获得了OneMax的最优解(所有位置上都是1)：[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

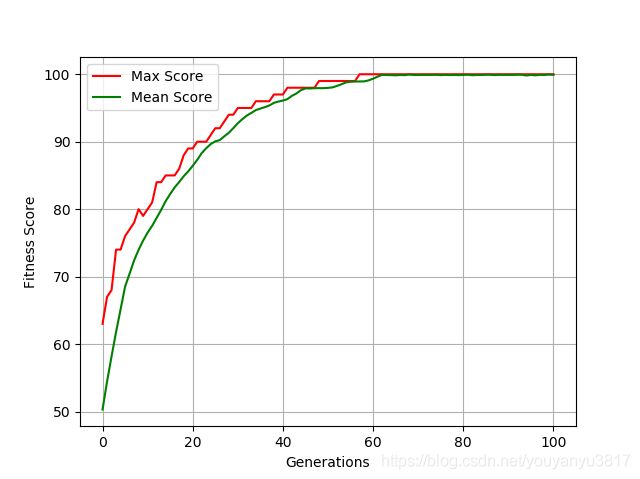
种群的进化过程如下图所示，我们可以观察到种群的进化速度由快到慢，且在61代左右停止进化，且在第58代时已经产生了最优解。

5. 完整代码

import random
import matplotlib.pyplot as plt
random.seed(39)
# 1. define individual and population
def CreateIndividual():
    return([random.randint(0,1) for _ in range(100)])

def CreatePopulation(size):
    return([CreateIndividual() for _ in range(size)])

# 2. define select, mate, mutate, evaluate function ----
# 2.1. define select function
def tournament(population,size):
    participants = random.sample(population,size)
    # evaluate function is defined in 3.4
    winner = max(participants,key=lambda ind:evaluate(ind))
    return(winner.copy())

def select(population,size):
    return([tournament(population,size) for _ in range(len(population))])

# 2.2. define mate function
def SinglePointCrossover(ind1,ind2):
    loc = random.randint(0,len(ind1)-1)
    genes1 = ind1[loc:]
    genes2 = ind2[loc:]
    ind1[loc:] = genes2
    ind2[loc:] = genes1
    return([ind1.copy(),ind2.copy()])

def mate(population,probability):
    new_population = []
    for i in range(0,len(population),2):
        ind1 = population[i].copy()
        ind2 = population[i+1].copy()
        if random.random() < probability:
            new_population.extend(SinglePointCrossover(ind1,ind2))
        else:
            new_population.extend([ind1,ind2])
    return(new_population)
# 2.3. define mutate function
def flipOneGene(ind):
    loc = random.randint(0,len(ind)-1)
    ind[loc] = 1 - ind[loc] # 0->1 or 1->0
    return(ind.copy())

def mutate(population,probability):
    new_population = []
    for ind in population:
        if random.random() < probability:
            new_population.append(flipOneGene(ind))
        else:
            new_population.append(ind.copy())
    return(new_population)
# 2.4. define evaluate function
def evaluate(individual):
    return(sum(individual))

# 2.5. define statistical metrics to monitor algorithm performance
def population_score_max(population):
    return(max([evaluate(ind) for ind in population]))

def population_score_mean(population):
    return(sum([evaluate(ind) for ind in population])/len(population))

# 3. Run genetic algorithm
def main(
    POPULATION_SIZE = 100,
    TOURNAMENT_SIZE = 3,
    CROSSOVER_PROB = 0.9,
    MUTATE_PROB = 0.1,
    MAX_GENERATIONS = 100
):
    generation = 0
    population = CreatePopulation(POPULATION_SIZE)
    max_scores = [population_score_max(population)]
    mean_scores = [population_score_mean(population)]
    best_individual = []
    while generation < MAX_GENERATIONS:
        population = select(population,TOURNAMENT_SIZE)
        population = mate(population,CROSSOVER_PROB)
        population = mutate(population,MUTATE_PROB)
        # collect statistics
        max_scores.append(population_score_max(population))
        mean_scores.append(population_score_mean(population))
        best_individual = max(
            best_individual,
            max(population,key=lambda ind: evaluate(ind))
        ).copy()
        generation += 1
    
    print("Best Solution:")
    print(best_individual)
    plt.plot(max_scores, color='red',label="Max Score")
    plt.plot(mean_scores, color='green',label="Mean Score")
    plt.legend()
    plt.xlabel("Generations")
    plt.ylabel("Fitness Score")
    plt.grid()
    plt.show()   

if __name__ == "__main__":
    main()

4.小结

为了深入的解释遗传算法，本文中没有使用任何的遗传算法包来解决OneMax问题。而下一期，我们会介绍DEAP(Distributed Evolutionary Algorithm in Python)包,并在之后的文章里用DEAP框架来解决遗传算法问题。

本人近期刚开始写文章，欢迎交流学习！