POJ 1904 King's Quest - from lanshui_Yang

Description

Once upon a time there lived a king and he had N sons. And there were N beautiful girls in the kingdom and the king knew about each of his sons which of those girls he did like. The sons of the king were young and light-headed, so it was possible for one son to like several girls. 

So the king asked his wizard to find for each of his sons the girl he liked, so that he could marry her. And the king's wizard did it -- for each son the girl that he could marry was chosen, so that he liked this girl and, of course, each beautiful girl had to marry only one of the king's sons. 

However, the king looked at the list and said: "I like the list you have made, but I am not completely satisfied. For each son I would like to know all the girls that he can marry. Of course, after he marries any of those girls, for each other son you must still be able to choose the girl he likes to marry." 

The problem the king wanted the wizard to solve had become too hard for him. You must save wizard's head by solving this problem. 

Input

The first line of the input contains N -- the number of king's sons (1 <= N <= 2000). Next N lines for each of king's sons contain the list of the girls he likes: first Ki -- the number of those girls, and then Ki different integer numbers, ranging from 1 to N denoting the girls. The sum of all Ki does not exceed 200000. 

The last line of the case contains the original list the wizard had made -- N different integer numbers: for each son the number of the girl he would marry in compliance with this list. It is guaranteed that the list is correct, that is, each son likes the girl he must marry according to this list. 

Output

Output N lines.For each king's son first print Li -- the number of different girls he likes and can marry so that after his marriage it is possible to marry each of the other king's sons. After that print Li different integer numbers denoting those girls, in ascending order.

Sample Input

4
2 1 2
2 1 2
2 2 3
2 3 4
1 2 3 4

Sample Output

2 1 2
2 1 2
1 3
1 4

    题目大意：有n个王子 和 n个美人 ， 一个王子可以喜欢几个美人，但是一个美人只能嫁一个王子，同时，一个王子也只能娶一个自己喜欢的美人。问：对于每个王子来说，他可以娶哪几个美人为妻，并且使其他王子也能娶到自己喜欢的美人。

    解题思路：这道题初看像二部图，但是按此思路想找不到解决办法。想想输入最后一行给出的一个完美匹配，应该有它的用处。

    先说一下如何建图：将每个王子u 和 他喜欢的美人 v 之间连一条有向边<u , v + n>(为避免顶点的序号混淆,将 美人的序号 +n 作为美人顶点的序号)，最后，通过输入中给出的一个完美匹配，将美人 v 与自己暂时的丈夫 u 之间连一条有向边<v + n , u>，建图完毕。

    然后，用tarjan求强连通分量，题目中样例建图如下，其中黑色边代表王子喜欢美人，红色边代表输入中给出的一个完美匹配 ：

用tarjan求出的强连通分量如下：

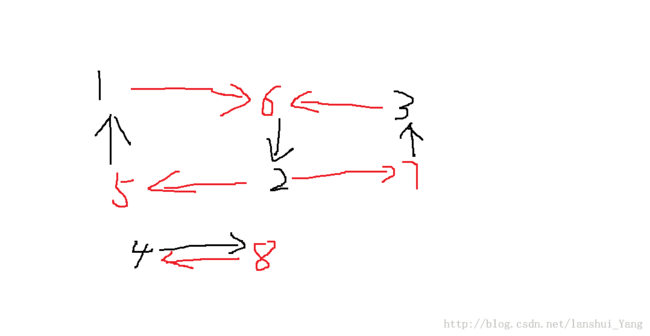
   从图中可以看出，每个强连通分量中顶点的个数都是偶数，每个王子可以与同自己喜欢的并且在一个强连通分量中的美人结婚，例如：如果 1 可以与 6 结婚，那么2 就会与5 结婚；如果1 与 5 结婚 ， 那么2 就会与 6 结婚 ；这两种方式均不影响3 和 4 。

   请看代码:

#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<set>
#include<vector>
#define mem(a , b) memset(a , b , sizeof(a))
using namespace std ;
const int MAXN = 4005 ;
vector<int> vert[MAXN] ; // 顶点
vector<int> fz[MAXN] ; // 记录每个强连通分量中的顶点
int ans[MAXN] ;
int n , m ;
bool vis[MAXN] ;
int dfn[MAXN] ;
int low[MAXN] ;
int id[MAXN] ;
int stap[MAXN] ;
int top ;
bool inq[MAXN] ;
int tmpdfn ;
int sumf ;  // 记录强连通分量个数
bool bi[MAXN] ;
inline void RD(int &a)
{
    a = 0 ;
    char t ;
    do
    {
        t = getchar();
    }
    while(t < '0' || t > '9') ;
    a = t - '0';
    while((t = getchar()) >= '0' && t <= '9')
        a = a * 10 + ( t - '0' );
}
inline void OT(int a)
{
    if(a >= 10)
    OT(a / 10) ;
    putchar(a % 10 + '0') ;
}
void clr()
{
    mem(vis , 0) ;
    mem(dfn , 0) ;
    mem(low , 0) ;
    mem(fz , 0) ;
    mem(inq , 0) ;
    mem(stap , -1) ;
    mem(id , -1) ;
    top = -1 ;
    tmpdfn = 0 ;
    sumf = 0 ;
    int i ;
    for(i = 0 ; i <= n * 2 ; i ++)
    {
        vert[i].clear() ;
        fz[i].clear() ;
    }
}
void tarjan(int u)
{
    vis[u] = 1 ;
    dfn[u] = low[u] = ++ tmpdfn ;
    stap[++ top] = u ;
    inq[u] = true ;
    int i ;
    for(i = 0 ; i < vert[u].size() ; i ++)
    {
        int v = vert[u][i] ;
        if(!vis[v])
        {
            tarjan(v) ;
            low[u] = min(low[u] , low[v]) ;
        }
        else if(inq[v])
            low[u] = min(low[u] , dfn[v]) ;
    }
    if(dfn[u] == low[u])
    {
        int tmp ;
        sumf ++ ;
        do
        {
            tmp = stap[top --] ;
            inq[tmp] = false ;
            id[tmp] = sumf ;
            fz[sumf].push_back(tmp) ;
        }
        while (tmp != u) ;
    }
}
void init()
{
    clr() ;
    int i ;
    int j ;
    int b ;
    for(i = 1 ; i <= n ; i ++)
    {
        int k ;
        RD(k) ;
        for(j = 0 ; j < k ; j ++)
        {
            RD(b) ;
            vert[i].push_back(b + n) ;
        }
    }
    for(i = 1 ; i <= n ; i ++)
    {
        int b ;
        RD(b) ;
        vert[b + n].push_back(i) ;
    }
}
void solve()
{
    int i ;
    for(i = 1 ; i <= n ; i ++)
    {
        if(!vis[i])
        {
            tarjan(i) ;
        }
    }
    int j ;
    int k ;
    for(i = 1 ; i <= n ; i ++)
    {
        int x = id[i] ;
        mem(bi , 0) ;
        int tp ;
        for(j = 0 ; j < fz[x].size() ; j ++)
        {
            tp = fz[x][j] ;
            bi[tp] = true ;
        }
        int p = 0 ;
        for(j = 0 ; j < vert[i].size() ; j ++)
        {
            tp = vert[i][j] ;
            if(bi[tp])
            ans[p ++] = tp ;
        }
        sort(ans , ans + p) ;
        OT(p) ;
        if(p > 0)
        putchar(' ') ;
        for(j = 0 ; j < p ; j ++)
        {
            OT(ans[j] - n) ;
            if(j < p - 1)
            putchar(' ') ;
        }
        putchar('\n') ;
    }
}
int main()
{
    while (scanf("%d" , &n ) != EOF)
    {
        getchar() ;
        init() ;
        solve() ;
    }
    return 0 ;
}