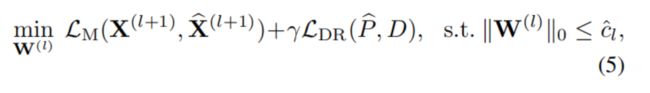双重回归学习：轻量化DRN网络---《Towards Lightweight Super-Resolution with Dual Regression Learning》

首先声明一下，根据我本人的理解，文章中对出现的Dual Regression做了不同翻译，除了涉及损失的时候会翻译成对偶回归损失，其余部分均译为双重回归，因为文中的损失部分是对偶的。此处读者暂且有个初步印象，具体情况见文章内容，便可理解。

目录

引言：

网络

双重回归网络------解决第一个问题

带有通道剪枝的轻量双重回归模型-----第二个问题

 基于双重回归的通道数搜索

基于双重回归的通道剪枝

实验

和SOTA方法的对比

模型剪枝方法的对比

Effect of Dual Regression Learning Scheme （消融实验dual regression learning scheme）

Effect of Dual Regression Channel Number Search 

Effect of Dual Regression Channel Pruning

Effect of Hyper-parameter λ in Eqn. (1) 

Effect of Hyper-parameter γ in Eqn. (5) 

Effect of Dual Regression on HR Data 

---

引言：

深度神经网络通过学习从低分辨率(LR)图像到高分辨率(HR)图像的映射，在图像超分辨率任务中表现出了显著的性能。

然而，由于SR问题本就是一个病态问题，现有的解决方法也存在着一些限制。

首先，SR可能的映射空间或许非常大，因为可能存在许多不同的HR图像，可以下采样到相同的LR图像。因此，很难从如此大的空间中直接学习一个还算满意的SR映射。

其次，通常不可避免地要开发具有极高计算成本的、大的模型，以获得还算不错的SR性能。由于SR映射空间非常大，现有的模型压缩方法很难准确识别冗余分量。

为了缓解第一个挑战，作者提出了一种双重回归学习（dual regression learning）方案来减少可能的SR映射的空间。

具体来说，除了从LR到HR图像的映射外，我们还学习了一个额外的对偶回归映射来估计下采样核以重建LR图像（类似CycleGan）。这样，对偶映射就可以作为一个约束来减少可能映射的空间。（空间大，那就想办法减少空间）

为了解决第二个挑战，作者又提出了一种轻量级双重回归压缩方法，以减少层级和通道级的冗余。

具体来说，作者首先开发了一种能够最小化对偶回归损失的通道数搜索方法，来确定每一层的冗余。根据搜索到的通道数，进一步利用双重回归方法来评估通道的重要性，并删掉冗余部分

网络

双重回归网络------解决第一个问题

由于原本就是病态问题，可能的SR映射函数的空间过大，使得训练十分困难。为了缓解这个问题，提出了一个双重回归学习框架通过在LR图像上引入一个额外的限制。

除了LR->HR的映射，也学习了一个相反的就是对偶映射从SR->LR。 换言之，在学习一个原始的映射P去重构HR图像的同时，也学习一个对偶映射D去重构LR图像。   原始的和对偶的任务构成了封闭的环去训练P和D模型。如果模型P生成的SR图像y’是正确的HR图像，那么，将y’放回D模型，会生成一个非常接近于输入的LR图像，即x’十分接近x。有了这个约束，便可以减少可能映射的函数空间，使其更容易学习更好的映射来重构HR图像。 对偶回归任务可以看做退化核的估计。

 这有点类似于CycleGan：但DRN是针对配对图像进行操作的，而CycleGan是针对于非配对，具体来说，CycleGan利用LR生成SR后，没有和HR的损失，而是计算循环一致损失，但是DRN会计算对偶回归损失。

CycleGAN使用循环来帮助最小化分布差异，但DRN构建循环来提高重构性能。

注：对于很多任务都是不能获得配对的训练数据，CycleGAN是一种在没有成对例子的情况下，学习将图像从源域X转换到目标域Y的方法。

其次，它们考虑了不同的循环映射。CycleGAN学习两个对称映射，但DRN考虑学习非对称映射。 

训练损失如下：λ 控制了双重回归损失的权重，其敏感性分析看下文

第一个问题：映射空间过大的问题解决完了，现在看第二个问题，压缩模型，模型过大的问题

带有通道剪枝的轻量双重回归模型-----第二个问题

大多数SR模型具有极高的计算成本，不能直接部署到计算资源有限的设备上。为了缓解这个问题，原本可以应用模型压缩技术来获得轻量级的模型。然而，由于极大的映射空间，准确地识别冗余部分（层或通道）并不容易。也就是说，一旦我们学习到一个不准确的SR映射，那可能会导致显著的性能下降。

为了进一步减少模型的冗余度，尽可能准确地学习映射，作者建立了一种基于通道剪枝技术的轻量级双重回归压缩方法，来压缩大型SR模型。

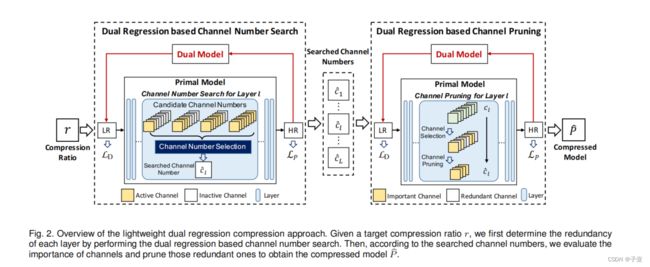
如图，分成左右两个部分进行介绍。

首先通过基于双重回归的通道数搜索来确定每一层的冗余。然后，利用基于双重回归的通道剪枝方案，来评估通道的重要性，并根据搜索到的通道数对冗余通道进行修剪，最后得到压缩模型。

 基于双重回归的通道数搜索

 大多数通道修剪方法采用手工的压缩策略来修剪深度模型，例如，在所有层中修剪50%的通道。然而，这样的压缩策略可能不是最优的，因为不同的层通常有不同的冗余。为了解决这一问题，我们提出了一种基于双重回归的通道数搜索方法，通过确定有望保留的通道数来识别每一层的冗余（换言之，通道数是代表可以保留下来的部分）。具体看算法1.

 

 

s.t.全称subject to，意思是使得...满足...

验证集的对偶回归损失满足最小化训练集的对偶回归损失 

基于双重回归的通道剪枝

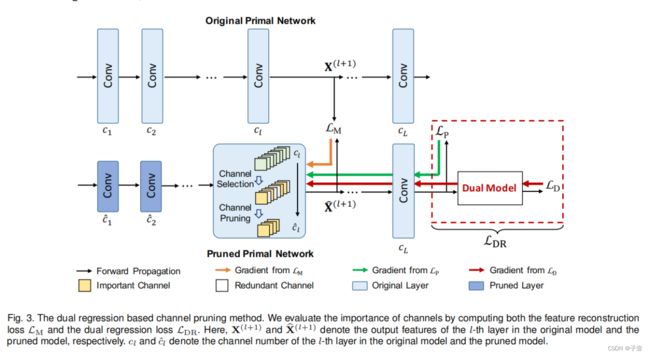
根据搜索的通道数，仍然需要确定哪些通道应该被修剪。其中一个关键的挑战是如何准确地评估通道的重要性。为了解决这个问题，作者开发了一种双重回归通道剪枝方法，利用双重回归方案来识别重要的通道。

需要通过计算特征重构损失和双重回归损失来评估通道的重要性。那重要性是怎么评估的呢？

 

L0范数是指向量中非0的元素的个数  

实验

首先提出了两个模型，包括小模型DRN-S和大模型DRN-L。

然后，作者使用所提出的双重回归压缩方法来压缩DRN-S模型。

考虑三种压缩比{30%、50%、70%}，得到三种轻量级SR模型，即DRN-S30、DRN-S50和DRN-S70。

实验分为一下几个方面：

· 和SOTA方法的对比

· 模型剪枝方法的对比

· Effect of Dual Regression Learning Scheme

· Effect of Dual Regression Channel Number Search

· Effect of Dual Regression Channel Pruning

· Effect of Hyper-parameter λ in Eqn. (1)

· Effect of Hyper-parameter γ in Eqn. (5)

· Effect of Dual Regression on HR Data （在HR图像上也添加了限制，观察结果）

和SOTA方法的对比

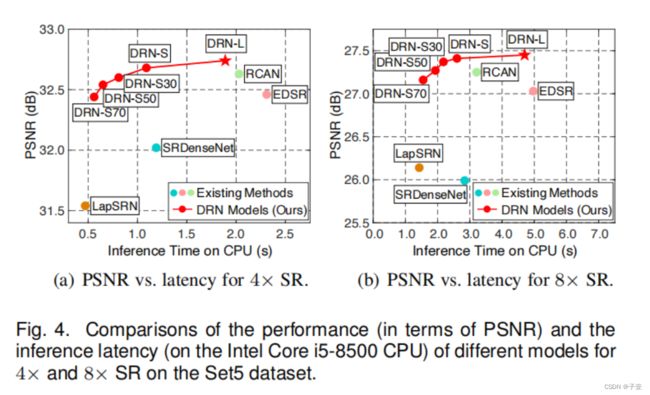
比对了定量X4和X8的PSNR、SSIM，还有定性的视觉效果，以及在CPU上的推理延迟

DRN-S以较小的延迟获得了良好的性能。当进一步压缩DRN-S模型时，压缩的DRN模型对模型推理更有效。

大型模型DRN-L在大多数基准数据集上都取得了最好的结果。当减少通道数和层数时，小基线模型DRN-S也获得了很好的性能。

经过压缩后，压缩DRN模型仍然能产生很好的性能。

 

 

作者的模型始终产生更清晰的边缘和形状（4×和8×SR） 

 

模型剪枝方法的对比

为了证明作者的压缩方法的有效性，比较了该轻量级双重回归压缩方法和几种现有的通道剪枝方法，包括CP，Thinet，和DCP。

CP：通道剪枝

Thinet：是结构化剪枝

DCP：鉴别力感知的通道剪枝（Discrimination-aware channel pruning）

应用所考虑的方法对4×和8×SR的DRN-S模型进行压缩。从表3中，鉴于相同的压缩比，作者提出的双重回归压缩方法得到的压缩SR模型始终优于其他方法得到的模型，并且其压缩模型始终具有较低的计算成本。

Effect of Dual Regression Learning Scheme （消融实验dual regression learning scheme）

这些结果表明，双重回归学习方案通过引入一个额外的约束来减少映射函数的空间，从而改进了HR图像的重建。

Effect of Dual Regression Channel Number Search 

设“Manually Designed”表示每层删除特定数量通道的压缩方法(每层删除30%通道)。“Automatically Searched”表示压缩方法可以自动搜索每一层的通道数。与“Manually Designed”得到的压缩模型相比，“Automatically Searched”得到的压缩模型其性能更高，计算成本更低。此外，通过双重回归通道数搜索，能够得到一个性能更好的轻量SR模型。

Effect of Dual Regression Channel Pruning

采用双回归通道剪枝方法，可以得到性能较好的轻量级SR模型。

以下两个参数的实验都是在证明对偶回归损失的效果，衡量其效果最大化。个人理解第一个是整体的对偶回归损失，第二个是剪枝部分局部的损失，前者包含后者。

Effect of Hyper-parameter λ in Eqn. (1) 

进行实验分析λ的有效性，它控制着双重回归损失的权重，作者分析了λ对4×SR的DRN-S和DRN-L模型的影响，并比较了模型在Set 5上的性能。 

将λ从0.001增加到0.1时，双重回归损失逐步展现出了更好的效果。如果进一步将λ增加到1或10，双重回归损失会过大最终阻碍性能。为了在原始回归和双重回归之间获得良好的权衡，最后在实践中设置了λ=0.1，用于所有DRN模型的训练

Effect of Hyper-parameter γ in Eqn. (5) 

γ控制着通道剪枝中双重回归损失的权重，具体来说，作者研究了γ对4×SR的三个压缩模型的影响，并比较了模型在Set5上的性能。

当γ设置为1时，压缩模型表现最好。增加或减少超参数γ，压缩的DRN产生更差的SR性能。因此，作者在实践中设置了γ=1来对DRN模型进行通道剪枝。

Effect of Dual Regression on HR Data 

实际上，也可以在HR域上添加一个约束条件来重建原始的HR图像。在本实验中，作者研究了双重回归损失对HR数据的影响，作者使用“DRN-S with dual HR”来表示模型，并对LR和HR图像进行回归 。

“DRN-S with dual HR” 比原始的模型多产生了两倍的计算成本，而性能提升的很有限，所以只在LR数据上使用了双重回归损失。