动手学习深度学习——2.6 概率论
2.6 概率论
在某种形式下,机器学习就是关于预测的。根据病人的临床病史,我们可以预测病人明年心脏病发作的概率。在异常检测方面,我们可能想要评估一下:如果飞机的喷气发动机正常工作的话,它的一系列读数可能性有多大。在强化学习中,我们希望代理人(agent)在一个环境中智能地行动。这意味着我们需要考虑在每个行动下获得高回报的可能性。当我们建立推荐系统时,我们也需要考虑概率。例如,假设我们为一家大型网上书店工作,我们可能需要估计特定用户购买特定书籍的概率。为此,我们需要使用概率的语言。整个课程、专业、论文、职业甚至院系都致力于概率。所以很自然地,我们这部分内容的目标不是教整个科目。相反,我们希望能让你们起步,教你们足够的知识,让你们能够开始建立你们的第一个深度学习模型,让你们对这门学科有足够的了解。如果你们愿意,你们可以开始自己探索它。
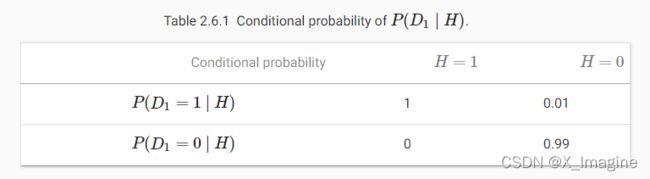
在前几节中,我们已经提到了概率,但没有明确说明它们的确切含义,也没有给出具体的例子。现在让我们更认真地考虑第一个例子:根据照片来识别猫和狗。这听起来可能很简单,但实际上是一个艰巨的挑战。首先,问题的难度可能取决于图像的分辨率。 现在考虑第二种情况:给定一些天气监测数据,我们想预测台北明天下雨的概率。如果是夏季,下雨的概率为0.5。 在这两种情况下,我们都有一些关注的值。在这两种情况下,我们都不确定最终的结果。但这两种情况之间有一个关键的区别。在第一个例子中,图像实际上要么是一只狗,要么是一只猫,我们只是不知道是哪一类。在第二种情况下,如果你相信这些事情(大多数物理学家都相信),结果可能实际上是一个随机事件。所以概率是一种灵活的语言用来推理我们的确定性水平,它可以在广泛的语境中有效地应用。 假设我们掷了一个骰子,想知道看到【1】而不是另一个数字的概率是多少。如果骰子是公正的,那么所有的【6】个结果 {1,…,6} 都是等可能发生的,因此我们会在【6】种情况中看到【1】。形式上,我们说【1】发生的概率是 1 6 \frac{1}{6} 61. 对于我们从工厂收到的真正的骰子,我们可能不知道这些比例,我们需要检查它是否被污染了。调查这个骰子的唯一方法就是多次投掷,并记录结果。对于每一次掷出的骰子,我们将观察到 {1,…,6} 中的一个值。给定这些结果,我们想要研究观察每个结果的概率。 对于每种情况的概率值,一种自然的方法是取该值的单个计数,并将其除以总抛掷次数。这给了我们一个给定事件概率的估计值。大数定律告诉我们,随着投掷次数的增加这个估计将越来越接近真实的潜在概率。在深入了解这里的细节之前,让我们先进行试验。 首先,让我们导入必要的包。 接下来,我们将进行掷骰子实验。在统计学中,我们把从概率分布中抽取样本的过程称为抽样。将概率分配给若干离散选择的分布称为多项分布。我们稍后会给出一个关于分布的更正式的定义,但是在更高的层次上,把它看作是事件的概率分配。 为了绘制单个样本,我们只需传递一个概率向量。输出是另一个相同长度的向量:它在索引【i】处的值是采样结果对应于【i】的次数。 如果运行采样器很多次,你会发现你每次得到的都是随机值。就像估计一个骰子的公平性一样,我们经常希望从相同的分布中生成许多样本。在 Python 循环中这样做会慢得难以忍受,所以我们使用的函数支持一次绘制多个样本,返回一个数组,其中包含我们想要的任意形状的独立样本。 现在我们知道了如何对一个骰子的滚动进行采样,我们可以模拟1000个滚动。然后我们可以仔细计算,在1000次滚动之后,每个数字被滚动了多少次。具体来说,我们计算相对频率作为真实概率的估计,具体代码如下: 因为我们是从一个公平的骰子中生成数据,所以我们知道每个结果的真实概率都是 1 / 6 1/6 1/6,大约是0.167,所以上面的输出估计看起来不错。 我们也可以想象这些概率是如何随着时间逐渐趋近于真实概率的。让我们进行500组实验,每组抽取10个样本。 当我们投掷骰子时,我们称 S = { 1 , 2 , 3 , 4 , 5 , 6 } S=\lbrace{1,2,3,4,5,6\rbrace} S={1,2,3,4,5,6} 为采样空间或者结果空间,每一个元素就是一个结果。一个事件(event)表示给定采样空间的一系列结果。比如在投掷骰子实验中,“seeing 5”,({5})和 “seeing an odd number”({1,3,5})都是有效的事件。值得注意的是,如果随机实验的结果在事件 A \mathcal A A 中,那么事件 A \mathcal A A 也算是出现。也就是说,骰子出现【3】,由于 3 ∈ { 1 , 3 , 5 } 3\in\lbrace1,3,5\rbrace 3∈{1,3,5},我们可以说事件 “seeing an odd number” 出现一次。 形式上,我们可以将概率看作是一个函数,它将一个集合映射为实数值。给定采样空间 S \mathcal S S,事件 A \mathcal A A 的概率记为 P ( A ) P(\mathcal A) P(A),并且满足如下的特性: 这些概率论公理是 Kolmogorov 1933 提出。由于这个公理系统,可以避免任何关于随机性的哲学争论。相反,我们可以用数学语言进行严格的推理。比如,令 A 1 \mathcal A_1 A1 代表整个采样空间, A i = ∅ , i > 1 \mathcal A_i=\varnothing,i>1 Ai=∅,i>1,我们可以证明 P ( ∅ ) = 0 P(\varnothing)=0 P(∅)=0,也就是不可能事件的概率为【0】. 在随机投掷骰子的实验中,引入了随机变量的概念。一个随机变量可以是任何数量,并且不是确定性的。它可以在随机实验的一组可能性中取一个值。考虑一个随机变量 X X X 的值存在于投掷骰子的采样空间 S = { 1 , 2 , 3 , 4 , 5 } \mathcal S=\lbrace1,2,3,4,5\rbrace S={1,2,3,4,5}. 我们可以称 “seeing a 5” 为 { X = 5 } \lbrace X=5\rbrace {X=5} 或者 X = 5 X=5 X=5,它的概率为 P ( { X = 5 } ) P(\lbrace X=5\rbrace) P({X=5}) 或者 P ( X = 5 ) P(X=5) P(X=5). 为了区分随机变量 X X X 和 X X X 的取值(比如取值 a),令 P ( X = a ) P(X=a) P(X=a). 但是,这种迂腐的做法导致了一种繁琐的表示法。为了紧凑的表示,一方面我们将 P ( X ) P(X) P(X) 称为随机变量 X X X 的概率分布:这个分布表示 X X X 取任何值的可能性。另一方面,我们也可以令 P ( a ) P(a) P(a) 表示随机变量的取值为【a】的概率。由于在概率理论中,一个事件是来自采样空间的一组结果,我们可以为随机变量指定一个范围的取值。比如, P ( 1 ⩽ X ⩽ 3 ) P(1\leqslant X \leqslant 3) P(1⩽X⩽3) 表示事件 { 1 ⩽ X ⩽ 3 } \lbrace 1\leqslant X \leqslant 3\rbrace {1⩽X⩽3} 的概率,也即是 { X = 1 , 2 , o r , 3 } \lbrace X=1,2,or,3\rbrace {X=1,2,or,3}. 等价地, P ( 1 ⩽ X ⩽ 3 ) P(1\leqslant X \leqslant 3) P(1⩽X⩽3) 表示随机变量 X X X 可以从 { 1 , 2 , 3 } \lbrace 1,2,3\rbrace {1,2,3} 取值的概率。 注意,离散型随机变量(比如骰子的面数)和连续型随机变量(比如人的身高)有着细微的差别。问两个人的身高是否完全相同没有任何意义。如果我们进行足够精确的测量,地球上不存在身高完全相同的人。事实上,如果进行精确测量,同一个人苏醒和睡觉时的身高也是不一样的。所以没有必要去问一个人身高为1.80139278291028719210196740527486202米的概率。考虑到世界人口的数量,这种可能性几乎为0. 问一个人的身高是否在一个区间(比如,介于1.79和1.81之间)似乎更加有意义。这种情况下,我们将可能性看作是一个值的概率密度。精确的【1.8】米没有可能性,但是具有非零密度。在任何两个不同的高度之间具有非零的概率。在接下来的章节中,我们考虑离散空间的概率。关于连续随机变量的内容,可以参考【18.6】。 很多情况下,我们通常一次考虑多个随机变量。例如,我们可能想建立疾病和症状之间关系的模型。如果给出一种疾病和一种症状,比如“流感”和“咳嗽”,那么这两种症状都有可能在患者身上发生,也有可能不发生。虽然我们希望两者的概率都接近于零,但我们可能想要估计这些概率以及它们之间的关系,以便我们可以应用我们的推论来实现更好的医疗护理。 作为一个更复杂的例子,图像包含数百万像素,因此具有数百万随机变量。在许多情况下,图像会附带一个标签,用来识别图像中的物体。我们也可以把标签看作是一个随机变量。我们甚至可以把所有的元数据看作是随机变量,比如位置、时间、光圈、焦距、 ISO、焦距和相机类型。所有这些都是共同发生的随机变量。当我们处理多个随机变量时,有几个数量是有意义的。 联合概率:事件A和事件B一起发生的概率,它是两个或多个事件相交的概率,记为 P ( A ∩ B ) P(A\cap B) P(A∩B)。 P ( A = a , B = b ) P(A=a,B=b) P(A=a,B=b) 称为联合概率。给定任何的值【a,b】,联合概率表示 A = a , B = b A=a,B=b A=a,B=b 同时发生的概率是多少?注意,对于任何值【a,b】, P ( A = a , B = b ) ⩽ P ( A = a ) P(A=a,B=b)\leqslant P(A=a) P(A=a,B=b)⩽P(A=a). 由于 A = a A=a A=a 和 B = b B=b B=b 发生,表示两者同时发生,那么自然小于 A = a A=a A=a 或者 B = b B=b B=b 发生的概率。 条件概率:在已知事件A已经发生的情况下,B事件将发生的概率,用 P ( B ∣ A ) P(B|A) P(B∣A) 表示。 比值: 0 ⩽ P ( A = a , B = b ) P ( A = a ) ⩽ 1 0\leqslant \frac{P(A=a,B=b)}{P(A=a)} \leqslant1 0⩽P(A=a)P(A=a,B=b)⩽1,这样的比值被称为条件概率,具体的定义形式为 P ( B = b ∣ A = a ) P(B=b|A=a) P(B=b∣A=a):表示在 A = a A=a A=a 发生的前提下, B = b B=b B=b 的概率。 利用条件概率的定义,我们可以推导出统计学中最有用和最著名的方程之一:贝叶斯定理。通过构造,我们得到乘法法则 P ( A , B ) = P ( B ∣ A ) P ( A ) P(A,B)=P(B|A)P(A) P(A,B)=P(B∣A)P(A). 根据对称性,得到 P ( A , B ) = P ( A ∣ B ) P ( B ) P(A,B)=P(A|B)P(B) P(A,B)=P(A∣B)P(B). 假设 P ( B ) > 0 P(B)>0 P(B)>0,求解其中一个条件变量,得到如下等式: 如果我们想从一件事推断出另一件事,比如因果关系,那么贝叶斯定理是非常有用的,但我们只知道相反方向的性质,我们将在本节后面看到。而边际化可以可以完成这个工作。这个操作就是:用 P ( A , B ) P(A,B) P(A,B) 决定 P ( B ) P(B) P(B). 我们可以看到,B 的概率等于 A 的所有可能选择并将所有的联合概率相加,等式如下: 另一个需要检查的有用属性是依赖性和独立性。A 和 B 两个随机变量是相互独立的,即 A 的一个事件的发生并不透露 B 的一个事件的发生的任何信息。这种情况下, P ( B ∣ A ) = P ( B ) P(B|A)=P(B) P(B∣A)=P(B). 统计学上通常记为 A ⊥ B A\bot B A⊥B. 根据贝叶斯理论,立刻可以得出 P ( A ∣ B ) = P ( A ) P(A|B)=P(A) P(A∣B)=P(A). 对于其它的所有情况,我们称 A , B A,B A,B 是相互依赖的。比如,一个骰子连续两次掷出是独立的。作为对比,电灯开关的位置和房间的亮度则不是(然而,它们并不是完全确定的,因为我们总是会遇到坏掉的灯泡、电源故障或坏掉的开关)。 由于 P ( A ∣ B ) = P ( A , B ) P ( B ) = P ( A ) P(A|B)=\frac{P(A,B)}{P(B)}=P(A) P(A∣B)=P(B)P(A,B)=P(A) 等价于 P ( A , B ) = P ( A ) P ( B ) P(A,B)=P(A)P(B) P(A,B)=P(A)P(B),两个随机变量相互独立当且仅当联合分布是各自分布的乘积。同样的,给定随机变量 C,两个随机变量 A 和 B是条件独立的当且仅当 P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) P(A,B|C)=P(A|C)P(B|C) P(A,B∣C)=P(A∣C)P(B∣C),可以写为 A ⊥ B ∣ C A\bot B|C A⊥B∣C. 让我们来检验一下我们的技能吧。假设一名医生对一名病人进行HIV检测。这个测试是相当准确的,如果病人是健康的,但报告他有病,失败的概率只有1%。此外,如果患者确实携带艾滋病毒,它也能检测出。我们用D1表示诊断(1表示阳性,0表示阴性例),用H表示HIV状态(1表示阳性,0表示阴性)。【表2.6.1】列出了这些条件概率。 注意,由于条件概率需要和为1,所以列的和均为1(但是行的和不是1)。如果检测结果呈阳性,让我们算出这个病人感染艾滋病毒的概率,也即是 P ( H = 1 ∣ D 1 = 1 ) P(H=1|D_1=1) P(H=1∣D1=1). 显然,这将取决于这种疾病的常见程度,因为它会影响错误警报的数量。假设人口很健康,比如 P ( H = 1 ) = 0.0015 P(H=1)=0.0015 P(H=1)=0.0015. 应用贝叶斯理论,我们需要边际化和乘法柜子,计算如下: 这样,我们得到如下等式: 换句话说,尽管使用了非常准确的检测方法,但患者真正感染艾滋病毒的几率只有13.06%。正如我们所看到的,概率可能是违反直觉的。 当病人听到这样可怕的消息时,该怎么办呢?病人很可能会要求医生进行另一项测试以获得清晰的结果。第二次测试具有不同的特性,不如第一次测试,如【表2.6.2】所示: P ( D 1 = 1 , D 2 = 1 ∣ H = 0 ) = P ( D 1 = 1 ∣ H = 0 ) + P ( D 2 = 1 ∣ H = 0 ) = 0.01 × 0.03 = 0.0003 (2.6.5) \begin{aligned} P(D_1=1,D_2=1|H=0)&=P(D_1=1|H=0)+P(D_2=1|H=0)\\ &=0.01\times0.03\\ &=0.0003 \end{aligned} \tag{2.6.5} P(D1=1,D2=1∣H=0)=P(D1=1∣H=0)+P(D2=1∣H=0)=0.01×0.03=0.0003(2.6.5) P ( H = 1 ∣ D 1 = 1 , D 2 = 1 ) = P ( D 1 = 1 , D 2 = 1 ∣ H = 1 ) P ( H = 1 ) P ( D 1 = 1 , D 2 = 1 ) = 0.98 × 0.0015 0.00176955 = 0.8307 (2.6.8) \begin{aligned} P(H=1|D_1=1,D_2=1)&=\frac{P(D_1=1,D_2=1|H=1)P(H=1)}{P(D_1=1,D_2=1)}\\ &=\frac{0.98\times0.0015}{0.00176955}\\ &=0.8307 \end{aligned} \tag{2.6.8} P(H=1∣D1=1,D2=1)=P(D1=1,D2=1)P(D1=1,D2=1∣H=1)P(H=1)=0.001769550.98×0.0015=0.8307(2.6.8) 也就是说,第二次测试让我们更加确信并非一切都很好。尽管第二个测试比第一个测试的准确性要低得多,但它仍然显著地提高了我们的估计。 为了总结概率分布的关键特征,我们需要一些评估方式。随机变量 X 的期望(或者平均值)定义如下: 它的平方根叫做标准差。随机变量的一个函数的方差是指该函数与该函数的期望的偏离程度,因为从该随机变量的分布中抽样得到不同的值 【x】:

正如【Fig 2.6.1】所示,人类很容易通过【160 X 160】的图像分辨率来识别猫和狗,【40 X 40】的分辨率会有一定的难度,而在【10 X 10】的分辨率下,几乎不可能分辨。换句话说,我们在很远的距离(分辨率会很低)区分猫和狗的能力可能接近于无知的猜测。概率为我们提供了一种正式的方式来推理,并给出确定性的程度。如果我们完全确定图像描绘的是一只猫,我们说对应的标签 y y y 是 “cat” 的概率 P(y=“cat”) 等于1。如果我们没有证据表明 y=“cat” 或 y=“dog”,那么我们可以说这两种可能性是一样的,即P(y=“cat”)=P(y=“dog”)=0.5。如果我们有足够的信心,但不确定图像描绘的是一只猫,我们可以指定概率为0.52.6.1 基本概率论
import torch
from torch.distributions import multinomial
from d2l import torch as d2l
# 概率向量(等概率事件)
fair_probs = torch.ones([6]) / 6
# 模拟投掷一次骰子实验
y = multinomial.Multinomial(1, fair_probs).sample()
print('y: ', y)
# 输出如下
y: tensor([0., 0., 0., 0., 1., 0.]) # 出现的点数为【5】
# 模拟投掷10次骰子实验
y = multinomial.Multinomial(10, fair_probs).sample()
print('y: ', y)
# 输出如下
y: tensor([0., 2., 3., 0., 1., 4.])
# 模拟投掷1000次骰子实验
counts = multinomial.Multinomial(1000, fair_probs).sample()
y1 = counts / 1000 # Relative frequency as the estimate
print('y1: ', y1)
# 输出如下
y1: tensor([0.1820, 0.1480, 0.1830, 0.1520, 0.1840, 0.1510])
# 可视化结果
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend()
d2l.plt.show()
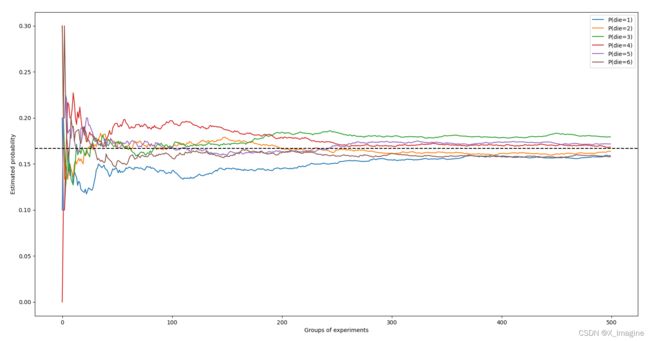
每条实曲线对应于骰子六个值中的一个,并给出了骰子在每组实验后出现该值的估计概率。虚线黑线表示真实的潜在概率。当我们通过进行更多的实验获得更多的数据时,6 条实曲线会向真实概率收敛(均接近黑色虚线)。2.6.1.1 概率论公理
2.6.1.2 随机变量
2.6.2 处理多随机变量
2.6.2.1 联合概率
2.6.2.2 条件概率
相关等式: P ( A , B ) = P ( A ) P ( B ∣ A ) P(A,B)=P(A)P(B|A) P(A,B)=P(A)P(B∣A)2.6.2.3 贝叶斯理论
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) (2.6.1) P(A|B)=\frac{P(B|A)P(A)}{P(B)}\tag{2.6.1} P(A∣B)=P(B)P(B∣A)P(A)(2.6.1)
注意,这里用的更加紧凑的写法, P ( A , B ) P(A,B) P(A,B) 表示联合概率, P ( A ∣ B ) P(A|B) P(A∣B) 表示条件概率。这样的分布可以用具体的值 A = a , B = b A=a,B=b A=a,B=b 来验证。2.6.2.4 边际化
P ( B ) = ∑ A P ( A , B ) (2.6.2) P(B)=\sum_AP(A,B)\tag{2.6.2} P(B)=A∑P(A,B)(2.6.2)
上面的等式也称为求和法则,边际化得到的概率或者分布也称为边际概率或者边际分布。2.6.2.5 独立性
2.6.2.6 实例应用
P ( D 1 = 1 ) = P ( D 1 = 1 , H = 0 ) + P ( D 1 = 1 , H = 1 ) = P ( D 1 = 1 ∣ H = 0 ) P ( H = 0 ) + P ( D 1 = 1 ∣ H = 1 ) P ( H = 1 ) = 0.01 × ( 1 − 0.0015 ) + 1 × 0.0015 = 0.011485 (2.6.3) \begin{aligned} P(D_1=1)&=P(D_1=1,H=0)+P(D_1=1,H=1)\\ &=P(D_1=1|H=0)P(H=0)+P(D_1=1|H=1)P(H=1) \\ &=0.01\times(1-0.0015)+1\times 0.0015\\ &=0.011485 \end{aligned} \tag{2.6.3} P(D1=1)=P(D1=1,H=0)+P(D1=1,H=1)=P(D1=1∣H=0)P(H=0)+P(D1=1∣H=1)P(H=1)=0.01×(1−0.0015)+1×0.0015=0.011485(2.6.3)
P ( H = 1 ∣ D 1 = 1 ) = P ( D 1 = 1 ∣ H = 1 ) P ( H = 1 ) P ( D 1 = 1 ) = 1 × 0.0015 0.011485 = 0.1306 (2.6.4) P(H=1|D_1=1)=\frac{P(D_1=1|H=1)P(H=1)}{P(D_1=1)}=\frac{1\times0.0015}{0.011485}=0.1306 \tag{2.6.4} P(H=1∣D1=1)=P(D1=1)P(D1=1∣H=1)P(H=1)=0.0114851×0.0015=0.1306(2.6.4)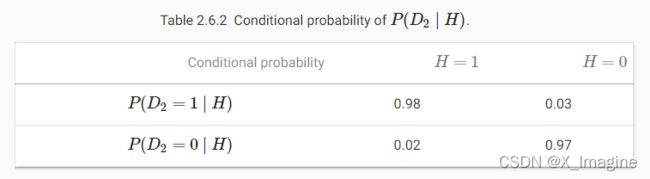
不幸的是,第二次测试也呈阳性。让我们通过假设条件独立性来计算出调用贝叶斯定理所需的概率:
P ( D 1 = 1 , D 2 = 1 ∣ H = 1 ) = P ( D 1 = 1 ∣ H = 1 ) + P ( D 2 = 1 ∣ H = 1 ) = 1 × 0.98 = 0.98 (2.6.6) \begin{aligned} P(D_1=1,D_2=1|H=1)&=P(D_1=1|H=1)+P(D_2=1|H=1)\\ &=1\times0.98\\ &=0.98 \end{aligned} \tag{2.6.6} P(D1=1,D2=1∣H=1)=P(D1=1∣H=1)+P(D2=1∣H=1)=1×0.98=0.98(2.6.6)
下面我们使用边际化和乘法规则如下:
P ( D 1 = 1 , D 2 = 1 ) = P ( D 1 = 1 , D 2 = 1 , H = 0 ) + P ( D 1 = 1 , D 2 = 1 , H = 1 ) = P ( D 1 = 1 , D 2 = 1 ∣ H = 0 ) P ( H = 0 ) + P ( D 1 = 1 , D 2 = 1 ∣ H = 1 ) P ( H = 1 ) = 0.0003 × 0.9985 + 0.98 × 0.0015 = 0.00176955 (2.6.7) \begin{aligned} P(D_1=1,D_2=1)&=P(D_1=1,D_2=1,H=0)+P(D_1=1,D_2=1,H=1)\\ &=P(D_1=1,D_2=1|H=0)P(H=0)+P(D_1=1,D_2=1|H=1)P(H=1)\\ &=0.0003\times0.9985+0.98\times0.0015\\ &=0.00176955 \end{aligned} \tag{2.6.7} P(D1=1,D2=1)=P(D1=1,D2=1,H=0)+P(D1=1,D2=1,H=1)=P(D1=1,D2=1∣H=0)P(H=0)+P(D1=1,D2=1∣H=1)P(H=1)=0.0003×0.9985+0.98×0.0015=0.00176955(2.6.7)
最后,最后,患者同时接受两项检测为阳性,进而确实为阳性的概率计算如下:2.6.3 期望与方差
E [ X ] = ∑ x x P ( X = x ) (2.6.9) E[X]=\sum_xxP(X=x)\tag{2.6.9} E[X]=x∑xP(X=x)(2.6.9)
当函数 f ( x ) f(x) f(x) 的输入是从分布 P 中抽取的随机变量时, f ( x ) f(x) f(x) 的期望值为:
E x ∼ p [ f ( x ) ] = ∑ x f ( x ) P ( x ) (2.6.10) E_{x\sim p}[f(x)]=\sum_xf(x)P(x)\tag{2.6.10} Ex∼p[f(x)]=x∑f(x)P(x)(2.6.10)
在许多情况下,我们度量随机变量【X】偏离其期望的程度,可以用方差衡量:
V a r [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − E [ X ] 2 (2.6.11) Var[X]=E[(X-E[X])^2]=E[X^2]-E[X]^2\tag{2.6.11} Var[X]=E[(X−E[X])2]=E[X2]−E[X]2(2.6.11)
V a r [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] (2.6.12) Var[f(x)]=E[(f(x)-E[f(x)])^2]\tag{2.6.12} Var[f(x)]=E[(f(x)−E[f(x)])2](2.6.12)