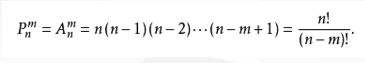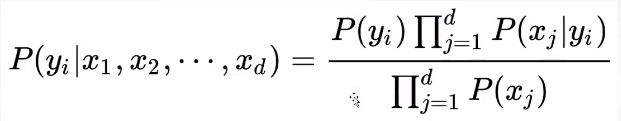深度学习之概率论总结
文章目录
- 一、事件
- 二、事件的运算
- 三、排列
- 四、组合
- 五、概率
-
- 5.1 古典概率
- 5.2 条件概率
- 5.3 联合概率
- 5.4 边缘概率
- 5.5 全概率
- 六、概率分布
-
- 6.1 伯努利分布
- 6.2 泊松分布
- 6.3 二项分布
- 七、高斯分布
-
- 7.1 3σ原则
- 7.2 标准正太分布
- 7.3 混合高斯分布
- 7.4 中心极限定理
- 7.5 高斯分布密度曲线
- 7.6 指数分布密度曲线
- 八、事件独立性
- 九、时间的互斥性
- 十、贝叶斯定理
- 十一、朴素贝叶斯
- 十二、深度学习的贝叶斯模型
- 十三、协方差
- 十四、参数估计
一、事件
● 随机事件
在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件)。
● 样本点
随机试验中的每一个可能出现的试验结果称为这个试验的一个样本点。
● 样本空间
样本空间:全体样本点组成的集合称为这个试验的样本空间Ω。
● 必然事件
必然事件:样本空间Ω也是其自身的一个子集,Ω也是一个“随机”事件,每次试验中必定有Ω中的一个样本点出现,必然发生。
● 不可能事件
不可能事件记作φ, 空集φ中也是样本空间的一个子集,φ中也是一个特殊的“随机”事件,不包含任何样本点,不可能发生。
● 空集
空集是指不含任何元素的集合。空集是任何集合的子集,是任何非空集合的真子集。空集不是无;它是内部没有元素的集合。
● 全集
如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集(通常也把给定的集合称为全集),通常记作U。
二、事件的运算
● 包含
➢包含:事件A是事件B的子事件,事件A发生必然导致事件B发生,事件A的样本点都是事件B的样本点, 记作ACB,也叫做A包含于B,或B包含A。
● 相等
➢相等:若ACB且BCA,那么A=B,称A和B为相等事件,事件A与事件B含有相同的样本点。
● 和事件
➢和事件:即事件A发生或事件B发生,事件A与事件B至少一个发生,由事件A与事件B所有样本点组成,记作AU B或A+B,也叫做A和B的并集。
● 积事件
➢积事件:即事件A和事件B同时发生,由事件A与事件B的公共样本点组成,记作AB或AnB,也叫做A和B的交集。
● 差事件
➢差事件:即事件A发生且事件B不发生,是由属于事件A但不属于事件B的样本点组成,记作A-B,也叫做A和B的差集。
● 互斥事件
➢互斥事件:事件A与事件B, 事件A与事件B不能同时发生,事件A与事件B没有公共的样本点。
● 事件A的对立事件
➢事件A的对立事件:对立事件是指其中必有一个发生的两个互斥事件。事件A不发生,事件A的对立事件是由不属于事件A的样本点组成,记作a,若在一个s集合中,a也可以叫做A的补集。
● 交换律
➢交换律: AUB=BUA、AB=BA
● 集合律
集合律: (AUB)∪C=AU(BUC)
● 分配率
➢分配律: AU( BC)=( AUB)(AUC); A( B∪C )=( AB)U(AC)
三、排列
● 概念
排列:从给定个数的元素中取出指定个数的元素进行排序。
四、组合
● 概念
组合:从给定个数的元素中取出指定个数的元素,不考虑排序。
五、概率
5.1 古典概率
● 概念
古典概率通常又叫事前概率,是指当随机事件中各种可能发生的结果及其出现的次数都可以由演绎或外推法得知,而无需经过任何统计试验即可计算各种可能发生结果的概率。
● 大数定理
大数定理:在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。重复次数越多,概率越准确。
● 抽样
抽样分为放回抽样和不放回抽样。
5.2 条件概率
● 概念
事件A在另外一个事件B已经发生条件下的发生概率,记为P(A|B)。
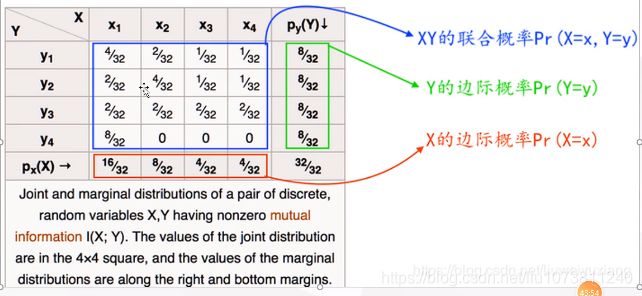
5.3 联合概率
● 概念
在多元的概率分布中多个随机变量分别满足各自条件的概率,记为P(AB)。
5.4 边缘概率
● 概念
在多元的概率分布中单个随机变量概率,记为P(A)。
5.5 全概率
● 概念
若事件A1,A2,…构成一个完备事件组且都有正概率,则对任意一个事件B,有如下公式成立:P(B)=P(BA1)+P(BA2)+…+P(BAn)=P(B|A1)P(A1) + P(B|A2)P(A2) + … + P(B|An)P(An).此公式即为全概率公式。
六、概率分布
● 概念
表述随机变量取值的概率规律。
● 简述
- 所有取值概率的和必须为1
- 随机变量的概率取值范围[0,1]
6.1 伯努利分布
6.2 泊松分布
6.3 二项分布
七、高斯分布
高斯分布又叫标准分布、误差分布。自然界的一切,人的身高,体重,五官,智商,等等。高斯分布的表示方法为N(μ, σ^2)
7.1 3σ原则
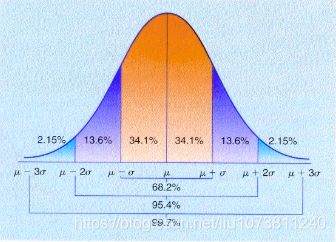
99.7%的概率值都落在了3σ范围内。采样的时候只需取到3σ之内就可以,缩小了范围,截断正太分布。均值控制左右移动,方差控制高低.
7.2 标准正太分布
推理:N(0, 1)*σ + u 任何正太分布都可以从标准正太分布采样后得到。
7.3 混合高斯分布
- 由每个单独的高斯分布组成的分布,也是一个高斯分布,称为混合高斯分布。
- 高斯分布的方差在这里变成了协方差矩阵的逆,要衡量各个分布之间的关系。
7.4 中心极限定理
● 概念
中心极限定理指的是给定一个任意分布的总体。每次从这些总体中随机抽取 n 个抽样,一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。
● 举例
现在我们要统计全国的人的体重,看看我国平均体重是多少。当然,我们把全国所有人的体重都调查一遍是不现实的。所以我们打算一共调查1000组,每组50个人。 然后,我们求出第一组的体重平均值、第二组的体重平均值,一直到最后一组的体重平均值。中心极限定理说:这些平均值是呈现正态分布的。并且,随着组数的增加,效果会越好。 最后,当我们再把1000组算出来的平均值加起来取个平均值,这个平均值会接近全国平均体重。
7.5 高斯分布密度曲线
7.6 指数分布密度曲线
● 概念
指数分布是两件事情发生的平均间隔时间,时间是连续变量。
八、事件独立性
● 概念
设A、B为随机事件,若同时发生的概率等于各自发生的概率的乘积,则A、B相互独立。
九、时间的互斥性
● 概念
➢设A、B为随机事件,A或B发生的概率等于分别发生概率的和,则A、B互斥。
十、贝叶斯定理
● 公式

P(B|A)是似然概率,P(A)是先验概率,P(B)是 全概率。P(A|B)是后验概率。
● 极大似然估计
极大似然估计可以拆成三个词,分别是“极大”、“似然”、“估计”,分别的意思如下:
极大:最大的概率
似然:看起来是这个样子的
估计:就是这个样子的
连起来就是,最大的概率看起来是这个样子的那就是这个样子的。
总结:极大似然估计就是在只有概率的情况下,忽略低概率事件直接将高概率事件认为是真实事件的思想。
● 学派
分为频率派和贝叶斯学派
● 贝叶斯定理与人脑
贝叶斯定理现在很多人都在研究,就是因为不少人相信贝叶斯定理和人脑的工作机制很像(此处颇多争论,望自行判断),因此称为机器学习的基础。比如,你和对方聊天的时候,如果对方说出”虽然“两个字,你大概会猜测,对方后继九成的可能性会说出”但是“。我们的大脑看起来好像是天生就在使用贝叶斯定理。
语法是人类后来总结出来的,我们天生是不需要语法就可以开口说话的,或许,人脑真的是贝叶斯大脑。最后,有一个小小的问题,根据我们的经验,硬币正反两面出现的概率都是0.5,如果我扔了一千次都是正面,那说明了什么?
十一、朴素贝叶斯
● 定义
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。
● 优点
- 算法逻辑简单,易于实现
- 分类过程中空间开销小。
● 缺点
理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
十二、深度学习的贝叶斯模型
● 公式
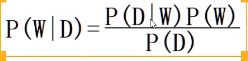
● 分析
P(W|D):深度学习模型在数据确定已知的情况下学习得到的W的概率(后验)。
P(D):每次采样输入模型的已知数据(全概率)。
P(D|W):开始假定(随机)的W下生成的数据,通过现有模型的W,得到现有数据D的概率,相当于把现有的数据D输入模型,在随机W下输出的结果的正确率,再通过输出结果的正确率,计算出这种正确率下输入的数据D的正确概率(似然)。
P(W):对开始的W的限定,假设W满足某种条件(先验)。
● 先验的应用
先验的应用: alphaGO的人类棋谱学习,鉴黄算法中对皮肤颜色像素占比的计算,关键点的计算。
十三、协方差
十四、参数估计
● 定义
从样本中来估计总体分布中未知参数的过程。
● 点估计
用样本统计量来估计总体参数,因为样本统计量为数轴上某一点值,估计的结果也以一个点的数值表示,所以称为点估计。点估计的方法有矩估计、最大似然估计、最小二乘法等。
矩估计通过期望和方差之间的换算来估计参数。
● 区间估计
通过从总体中抽取的样本,根据一定的正确度与精确度的要求,构造出适当的区间,以作为总体的分布参数(或参数的函数)的真值所在范围的估计)