论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification
学习自我训练的半监督小样本分类
Li-nips2019-LST-Learning to Self-Train for Semi-Supervised Few-Shot Classification
摘要
作者提出了一种新颖的半监督元学习方法:学习自我训练(简称 LST)。这种方法利用无标签数据,特别是学习如何择优挑选和标记这些无标签数据,以进一步提高性能。对于每个小样本任务,训练一个小样本模型来预测无标签数据的伪标签,然后对有标签和伪标签数据的自训练步骤进行迭代,每一步都进行调优。还学习了一个软权重网络(简称 SWN)来优化伪标签的自我训练权重,如此一来,更好的权重能够对梯度下降优化有更多的贡献。(这个软权重网络,软在哪里?如何学习的?)。在半监督小样本分类的两个 ImageNet 基准上进行评估,取得了很大改进超过最先进的方法。(很大改进是多大?最先进的方法是什么方法?)。
代码在 https://github.com/xinzheli1217/learning-to-self-train
1 引言
元学习是最强的小样本学习方法之一,在元学习策略中,基于梯度下降的方法特别有前景。另一个有趣的想法是利用额外的无标签数据。半监督学习在有标签的小样本数据上利用无标签数据,在标准数据集上取得了很好的性能。一个经典、直观、简单的方法是自训练(self-training)。自训练是一种常见的半监督算法:首先利用有标签数据训练一个监督模型,然后基于无标签数据的最可信的预测标签(称为伪标签)来扩大这个有标签数据集,其性能可超过基于正则化的方法(都有哪些? entropy minimization、Temporal ensembling、Virtual adversarial training),尤其是有标签数据非常稀少时。
因此,本文聚焦于半监督小样本分类任务:用于训练分类器的有标签数据很少而无标签数据很多。为了处理这个问题,作者提出了一个新方法:学习自我训练(LST),成功地把性能良好的半监督方法嵌入到元学习模式中。然而,这并不简单,因为直接递归地应用自训练会导致逐渐漂移,从而增加有噪声的伪标签。为了解决这个问题,首先通过元学习一个软权重网络(SWN)来自动地减少噪声标签的影响,而且在每个自训练步骤之后对只有已标记数据的模型进行调优。
特别地,作者的 LST 方法包括内循环自训练(针对一个任务)和外循环元学习(针对所有任务)。LST 的元学习针对每个任务不但学习初始化自训练模型而且学习怎样挑选噪声标签。内循环:首先利用元学习到的初始化方法,使一个特定任务模型快速适应很少有标签数据的情况,然后用该模型预测伪标签,最后通过元学习到的软权重网络(SWN)给标签添加权重。在外循环中,这些元学习器的性能通过一个独立的验证集进行评估,并利用对应的验证损失进行参数优化。
本文的贡献有三个:
- 一种新的自训练策略,能够避免标签噪声导致的模型漂移,实现健壮的递归训练。
- 一种新的元学习择优挑选方法,能够优化伪标签的权重,特别是快速有效的自我训练。
- 在两个版本的 ImageNet 基准测试上(miniImageNet 和 tieredImageNet)进行了广泛的实验,达到了最佳性能。
2 相关工作
小样本分类(FSC),半监督学习(SSL),半监督小样本分类(SSFSC)。
3 问题定义和符号表示
小样本分类任务的构成:
- 支持集 S:有标签
- 查询集 Q:没见过的样例
- 无标签数据 R:用于半监督学习,可能包含干扰类(S 中没有的类别)
元学习与传统分类的区别:
- 1 主要阶段是元训练和元测试(而非训练和测试),本文的训练还包括自训练。
- 2 元训练和元测试中的样例不是数据点而是片段(小样本学习任务)。
- 3 元学习的目标不是对没见过的数据点进行分类,而是让分类器快速适应新的任务。
元学习的符号表示:
- D:数据集
- T:小样本分类任务
- S:支持集,类别少且样例少,例如5个类别,每个类别1个样例。
- R:无标签样例集,大量样例。
- Q:查询集,用于计算验证损失,优化元学习器。
元测试的符号表示:
- D u n D_{un} Dun:之前没见过的数据集(与 D 中的样例类别没有重叠)。
- T u n T_{un} Tun:小样本分类任务
- S u n S_{un} Sun:支持集
- R u n R_{un} Run:无标签样例集
- Q u n Q_{un} Qun:查询集
4 学习自我训练(LST)
图1:LST 方法在单个任务上的流程。一个类别的原型是该类别中的样例特征均值,SWN 是软加权网络,其优化过程在图2和4.2节给出。
图2:LST 方法中的外循环和内循环训练流程。红色方框中的内循环包括 m 步再训练(用 S 和 R p R^p Rp)、T-m 步调优(只用 S)。在迭代训练中,用调优后的 θ T \theta_T θT 替换 MTL 学到的初始 θ T \theta_T θT(参见4.1节)用于下个阶段的伪标签。
LST 方法在单个任务上的流程如图1 所示,包括:
- 给无标签样例“打伪标签”(利用预训练的小样本模型);
- 通过硬挑选和软加权,“择优挑选”打了伪标签的样例;
- 在选出的样例上“再训练”,调优;
- 在查询集上进行“最终测试”。
在一个元训练任务上,“最终测试”作为一个验证输出一个 loss 用于优化 LST 的元学习参数,如图2所示。
4.1 给无标签数据打上伪标签,择优挑选无标签数据
打伪标签
采用小样本学习的监督学习方法训练一个特定于任务的分类器 θ \theta θ,然后用 θ \theta θ 预测无标签数据集 R 的伪标签。从根本上说,可以使用多种方法来训练 θ \theta θ。作者选择了一种表现最好的方法:元迁移学习(MTL),是基于梯度下降进行优化。在外循环元学习中,MTL 学习缩放和移动参数 Φ s s \Phi_{ss} Φss ,使得预训练的大规模神经网络 Θ \Theta Θ(例如,对于 miniImageNet 上的 64 个类别,每个类别 600 张图片)快速适应新的学习任务。在内循环的基础学习中,MTL 把最后的全连接层作为分类器 θ \theta θ 并用 S 来训练它。
在一个任务 T 上,打伪标签的过程:
其中 t ∈ { 1 , . . . , T } t\in\{1,...,T\} t∈{1,...,T} 是迭代索引。通过元学习到的 θ ′ \theta' θ′(参见4.2节)给出初始模型 θ 0 \theta_0 θ0。
其中 f 表示分类函数,具有参数 θ T \theta_T θT 和具有参数 Φ s s \Phi_{ss} Φss 的特征提取器(为了简化,忽略了冻结的 Θ \Theta Θ(不再训练))。
择优挑选
由于直接在伪标签数据上进行自训练会导致逐渐漂移(由标签噪声引起),作者提出了两个对策。
第一个对策是,元学习 SWN 自动调整数据点,给更有前途的样例增加权重,让那些前景不光明的样例减少权重,即学会择优挑选。在此步骤之前,还执行了硬挑选,只使用最确信的预测值。
第二个对策是,在每个自训练步骤之后,只用带标签的数据(在 S 中)调优模型(参见4.2节)。
具体地说,根据 Y R Y^R YR 的可信分数来挑选每个类别的前 Z 个样例,因此,在这个伪标签数据集中,从 C 个类别中得到 Z × C Z\times C Z×C 个样例,称为 R p R^p Rp。在用 R p R^p Rp 进行再训练之前,通过一个元学习到的软加权网络(SWN)计算它们的软权重,以减少噪声标签的影响。这些权重应该反映伪标签样例和 C 个类别表征之间的关系或距离。作者参考了一个监督学习方法,称为关系网络(RelationNets),利用传统小样本分类的支持样例和查询样例之间的关系。
首先,计算每个类别的原型特征,取其所有样例特征的平均值。对于 1-shot 的情况,使用唯一的样例特征作为原型。然后,给定一个伪标签样例 ( x i , y i ) ∈ R p (x_i,y_i)\in R^p (xi,yi)∈Rp,连接其特征与 C 个原型特征,再把它们输入 SWN。第 c 个类别上的权重如下:
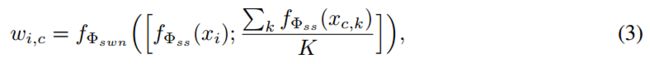
其中 c ∈ { 1 , . . . , C } c\in\{1,...,C\} c∈{1,...,C} 是类别索引, k ∈ { 1 , . . . , K } k\in\{1,...,K\} k∈{1,...,K} 是样例索引, x c , k ∈ S x_{c,k}\in S xc,k∈S, Φ s w n \Phi_{swn} Φswn 是 SWN 的参数(其优化过程参见4.2节)。注意: w i , c w_{i,c} wi,c 在 C 个类别上已被归一化(通过 SWN 中的 softmax 层)。
4.2 在择优挑选的数据上进行自我训练
如图2(内循环)所示,自训练包括两个主要阶段:
- 第一个阶段,包括多步再训练,在伪标签数据上(与支持集一起使用)。
- 第二个阶段,只用 S 进行多步调优。
首先,初始化分类器参数 θ 0 ← θ ′ \theta_0\leftarrow\theta' θ0←θ′,先前的外循环中的任务对 θ ′ \theta' θ′ 进行了元优化。然后通过 R p R^p Rp 和 S 上的梯度下降来更新 θ 0 \theta_0 θ0。假设有 T 步迭代,1~m 步迭代是再训练,m+1~T 步迭代是调优。对于 t ∈ { 1 , . . . , m } t\in\{1,...,m\} t∈{1,...,m} 有:
![]()
其中 α \alpha α 是基础学习率,L 是分类损失(对于来自不同集合的样本是不同的),公式如下:
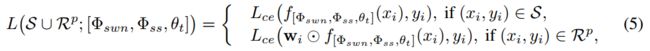
其中 L c e L_{ce} Lce 是交叉熵损失(在 S 上通过标准方法计算)。
对于 R p R^p Rp 中的一个伪标签样例,在将其送入 softmax 层之前,先通过 w i = { w i , c } c = 1 C w_i=\{w_{i,c}\}_{c=1}^C wi={wi,c}c=1C 对其预测值进行加权。对于 t ∈ { m + 1 , . . . , T } t\in\{m+1,...,T\} t∈{m+1,...,T},在 S 上对 θ t \theta_t θt 进行调优:
![]()
利用调优后的模型进行自训练迭代
传统的自训练通常遵循一个迭代过程,目的是获得一个逐渐扩大的有标签数据集。相似地,一旦得到优化好的模型,本文的方法也可以被迭代,即利用 θ T \theta_T θT 在 R 上预测更好的伪标签并再训练 θ \theta θ 一遍。有两种情境:
- [1] R 较小,例如,每个类 10 个样例,因此自训练只能在相同的数据上重复;
- [2] R 无限大(至少足够大,例如,每个类 100 个样例),可将其拆分为多个子集(例如,10 个子集,每个子集 10 个样例),每次在新的子集上执行递归学习。
本文考虑第二种情境,而且通过实验验证,先拆分子集再递归训练,比用整个数据集 re-training 一轮更好。
元优化 Φ s w n \Phi_{swn} Φswn, Φ s s \Phi_{ss} Φss 和 θ ′ \theta' θ′
基于梯度下降的方法通常使用 θ T \theta_T θT 计算查询集上的验证损失用于优化元学习器。本文有多个元学习器,参数为 Φ s w n \Phi_{swn} Φswn, Φ s s \Phi_{ss} Φss 和 θ ′ \theta' θ′,通过在不同的自训练阶段计算的验证损失更新这些参数,目的是为了达到特定的目的而优化这些参数。 Φ s s \Phi_{ss} Φss 和 θ ′ \theta' θ′ 用于特征提取和最后的分类,影响整个自训练,用最终模型 θ T \theta_T θT 的损失来优化这两个参数。而 Φ s w n \Phi_{swn} Φswn 产生软权重用于优化“再训练”步骤,其好坏应该通过“再训练”分类器 θ m \theta_m θm 来评估,因此用 θ m \theta_m θm 的损失来优化该参数。两个优化函数如下:
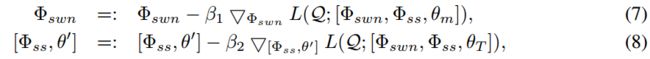
其中 β 1 \beta_1 β1 和 β 2 \beta_2 β2 是元学习率,都是在实验中手动设置。
5 实验
两个基准测试,设置细节,与最先进的方法进行比较,一个消融实验。
5.1 数据集和实现细节
数据集
ImageNet 的两个子集:miniImageNet 和 tieredImageNet。小样本分类任务设置 5-way, 1-shot (5-shot),查询集每个类别的样例数统一用 15,无标签集 R 每个类别的样例数是 30(50),从中“硬挑选” 20(30) 个确信样例用于软加权以及再训练。在递归训练中,使用一个更大的无标签数据池,包括 100 个样例,每次迭代都从里面采样一些样例,即 30(50) 个样例对于 1-shot (5-shot) 任务。
网络架构
Θ \Theta Θ 和 Φ s s \Phi_{ss} Φss 的网络架构是基于 ResNet-12,由 4 个残差块组成,每个残差块有 3 个卷积层(具有 3 × 3 3\times 3 3×3 的卷积核),每个残差块的最后是一个 2 × 2 2\times 2 2×2 的最大池化层。过滤器的数量从 64 开始,每到下一残差块就翻倍。在这些残差块之后,是一个平均池化层把特征图压缩为一个 512 维的特征向量。SWN 的架构,包括2 个卷积层( 3 × 3 3\times 3 3×3 的卷积核),64 个过滤器,2 个全连接层(维度分别是 8 和 1)。
超参数
基础学习率 α \alpha α(在式1, 式4, 式6中)设置为 0.01,元学习率 β 1 \beta_1 β1 和 β 2 \beta_2 β2(在式7, 式8中)初始设置为 0.001,每迭代 1k 轮,衰减为之前的一半,直到最小值 0.0001。batch size 为 2,迭代 15k 轮。在递归训练中,对于 1-shot (5-shot) 任务使用 6 (3) 个递归阶段。每个递归阶段包括 10 步“再训练”和 30 步调优。
比较方法
就 SSFSC 而言,可用来进行比较的模型有两个:软屏蔽 K 均值(Soft Masked k-Means)、TPN。这两个模型都用预训练的卷积神经网络进行特征提取。为了公平比较,作者实现了 MTL 作为这两个模型的组件,实验证明这样更好。另外,使用无标签数据的最大预算(每个类 100 个样例)运行这些实验。还比较了哪些与本文模型密切相关的最先进的监督 FSC 模型,它们基于数据增广或梯度下降。
消融设置
为了展示本文模型的效果,作者设计了两组实验设置:有元训练、无元训练。下面是消融设置的细节:
- no selection 表示一次自训练的基线,不挑选任何伪标签。
- hard 表示硬挑选伪标签。
- hard with meta-training 表示只对 [ Φ s s , θ T ] [\Phi_{ss},\theta_T] [Φss,θT] 进行元学习。
- soft 表示通过元学习到的 SWN 在挑选的伪标签上进行软加权。
- recursive 表示进行自训练的多轮迭代,来优化模型,参见4.2节。注意,这个 recursive 只是针对元测试任务,因为元学习到的 SWN 可被重复使用。
- mixing 是一个与 recursive 可比的设置,混合所有的无标签子集用于 recursive,只运行一轮“再训练”(参见4.2节的倒数第二段)。
5.2 结果和分析
表1:miniImageNet 和 tieredImageNet 数据集上的 5-way, 1-shot 和 5-shot 分类准确率(%)。“pre” 表示使用所有的训练数据对一个单独的分类任务进行预训练。请注意,这是一个参考表,用于展示本文的模型通过考虑无标签数据获得了多少性能提升。
![论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification_第4张图片](http://img.e-com-net.com/image/info8/bc46262b93bd45bb9f28cab05b3506b3.jpg)
表2:消融实验(表格中部)和相关模型(表格下部)在 miniImageNet (“mini”) 和 tieredImageNet(“tiered”) 数据集上的分类准确率(%)。“fully supervised” 表示使用了无标签数据的标签。“w/D” 表示使用来自 3 个干扰类的无标签数据。
![论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification_第5张图片](http://img.e-com-net.com/image/info8/6843b9c980d34e739d64c2191963d010.jpg)
图3:使用不同的“再训练”步骤数,在 1-shot miniImageNet 上的分类准确率。例如 m=2 表示在每个递归阶段(总共40 步)进行 2 步“再训练”和 38 步调优。每个曲线展示的是最后一个阶段的结果。(a) 是本文提出的模型,(b) 是 recursive, hard (no meta) with MTL,© 是 recursive, hard (no meta) 只是用预训练的 ResNet-12 模型进行了初始化。
![论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification_第6张图片](http://img.e-com-net.com/image/info8/a1b30c091fc54892ad28513ee25544ce.jpg)
图4:使用不同数量的干扰类,在 miniImageNet 1-shot (a) 和 tieredImageNet 1-shot (b) 上的分类准确率

表3:Pseudo-labeling accuracies (%) during the meta-training process, on miniImageNet 1-shot.

表4:Pseudo-labeling accuracies (%) at six recursive stages of meta-test, on miniImageNet 1-shot. Stage-1 is initialization.
6 结论
【本期作者主页】https://blog.csdn.net/jieming2002
![论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification_第1张图片](http://img.e-com-net.com/image/info8/f800fa545b8148248d4ddc21df62cf59.jpg)
![论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification_第2张图片](http://img.e-com-net.com/image/info8/264b31efb5c04d94a73410cf11156806.jpg)

![论文阅读笔记 [NIPS2019] Learning to Self-Train for Semi-Supervised Few-Shot Classification_第3张图片](http://img.e-com-net.com/image/info8/eb8fa1ce848d44faaca1e3622689298f.jpg)