时间序列(三):ARIMA模型实战
时间序列系列文章:
时间序列(一):时间序列数据与时间序列预测模型
时间序列(二):时间序列平稳性检测
时间序列(三):ARIMA模型实战
什么是 ARIMA模型
ARIMA模型的全称叫做自回归移动平均模型,全称是(ARIMA, Autoregressive Integrated Moving Average Model)。也记作ARIMA(p,d,q),是统计模型(statistic model)中最常见的一种用来进行时间序列预测的模型。
ARIMA模型是一种自回归模型,只需要自变量即可预测后续的值。ARIMA模型要求时序数据是稳定的,或者经过差分处理后稳定,如果不稳定的数据,是无法捕捉到规律的。比如股票数据用ARIMA无法预测的原因就是股票数据是非稳定的,常常受政策和新闻的影响而波动。
ARIMA模型步骤
- 时间序列的获取与预处理:对于得到的时间序列数据,首先应该检查数据质量,例如是否有缺失,异常值的存在。确保数据无误后需要进行稳定性检验和白噪声检验。能够适用ARMA模型进行分析预测的时间序列必须满足的条件是平稳非白噪声序列。因此对数据的平稳性进行检验是时间序列分析的重要步骤。具体的检验方法可以查看上一篇文章 时间序列(二):时间序列平稳性与白噪声检测
- 模型定阶: 确定模型的类型并确定模型的参数
- 建模预测:使用模型进行建模并进行相关预测。
- 模型的验证: 模型的验证主要是验证模型的拟合效果,之后对模型进行相关优化与应用
时间序列的获取与预处理
导入数据
在本文中我们使用2015/1/2-2015/2/6某餐厅的销售数据进行建模。数据文件可以在公众号:Smilecoc的杂货铺 中回复时间序列获取。可直接扫描文末二维码关注!
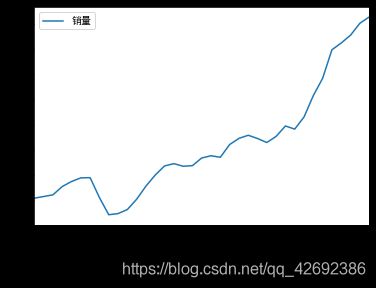
首先读入数据并查看一下时序图
import pandas as pd
discfile = 'arima_data.xls'
data = pd.read_excel(discfile, index_col = u'日期')
#时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
data.plot()
plt.show()
平稳性检验
从上述时序图中我们可以看到序列有明显的上升趋势,基本可以确定不是平稳序列了。
再通过自相关图检验一下:
#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
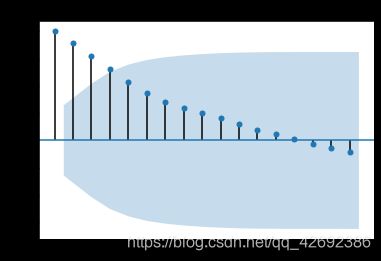
从自相关图从右向左看,时间序列随着阶数的递增,自相关系数缓慢衰减至0,不符合平稳序列的要求。
之后再对序列进行ADF检验,
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为:', ADF(data[u'销量']))
单位根检验统计量对应的p值显著大于0.05, 最终将该序列判断为非平稳序列
利用差分平稳数据
首先我们对时间序列数据进行一阶差分(一般情况下差分的阶数不会超过两阶,如果差分阶数过高会导致信息丢失较多导致预测误差较大).代码如下所示:
#一阶 差分
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plt.show()
之后我们再次对差分后的序列进行平稳性检测:
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() #偏自相关图
print(u'差分序列的ADF检验结果为:', ADF(D_data[u'销量差分'])) #ADF检测
从检验结果来看在一阶差分后已经是平稳序列,符合后续建模要求
模型定阶
再对数据进行预处理后得到平稳时间序列后我们就可以确定ARIMA模型相关的参数。
ARIMA有三个参数,可表示为ARIMA(p, d, q)。p为自回归阶数,也就是我们需要用前多少个时间段的数据去做自回归。d为时间成为平稳时所做的差分次数,q为移动平均阶数。在之前的平稳性变化中我们做了一阶差分,那么对应d=1,那么另外两个参数ARMA(p, q)如何确定呢?
通过自相关图或者偏相关图
在上述的平稳性检验的过程中我们得到了相关的自相关图和偏自相关图:
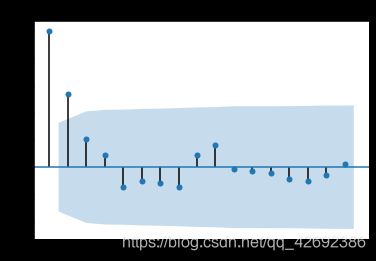
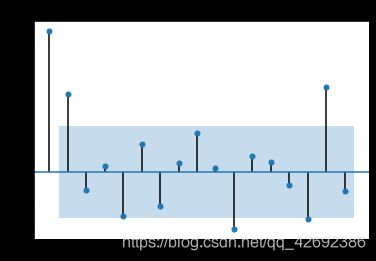
上面两幅图中,阴影部分为置信区间。
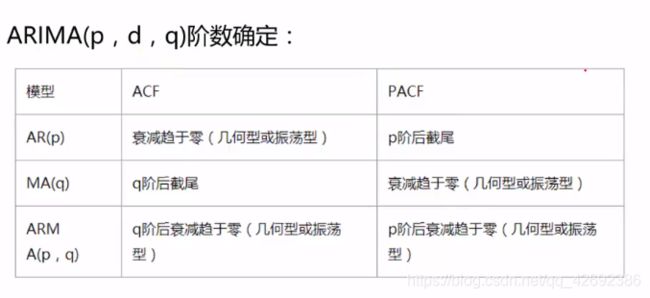
拖尾指序列以指数率单调递减或震荡衰减,而截尾指序列值落在置信区间内(95%的点都符合该规则).
根据上述自相关图与偏自相关图,我们有以下模型可以供选择:
- ARMA(0,1)模型:即自相关图在滞后1阶之后缩小为0,且偏自相关缩小至0,则是一个阶数q=1的移动平均模型;
- ARMA(3,0)模型:即偏自相关图在滞后3阶之后缩小为0,且自相关缩小至0,则是一个阶层p=3的自回归模型;
- ARMA(3,1)模型:即使得自相关和偏自相关都缩小至零。则是一个混合模型。
针对这三种模型,我们后续可以通过建立模型预测后并利用测试数据检验哪个模型更好, 同时我们也可以通过查看三种模型的AIC,BIC等信息来确定哪个模型更好。AIC,BIC都是判断模型的标准,其值越小表示模型越好。
AIC :赤池信息量 ,公式为: A I C = 2 k − 2 l n ( L ) AIC= 2 k-2 ln(L) AIC=2k−2ln(L)
BIC:贝叶斯信息量,公式为: B I C = l n ( n ) ∗ k − 2 l n ( L ) BIC=ln(n)*k-2 ln(L) BIC=ln(n)∗k−2ln(L)
其中k为模型参数个数,n为样本数量,L为似然函数
例如我们通过BIC判断相关模型的好坏的相关代码为:
print(ARIMA(data, (p,1,q)).fit().bic)
通过遍历获取
在上述通过自相关图与偏自相关图确定p,q的方法里,我们可以看到确定的参数不止一种,因此我们可以通过遍历各个p,q参数获取对应的AIC,BIC等信息确定参数。
#遍历
from statsmodels.tsa.arima_model import ARIMA
data[u'销量'] = data[u'销量'].astype(float)
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try: #存在部分报错,所以用try来跳过报错。
tmp.append(ARIMA(data, (p,1,q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp)
#输出BIC结果矩阵
bic_matrix = pd.DataFrame(bic_matrix) #从中可以找出最小值
print(bic_matrix)
结果中对应BIC最小的p值和q值为:0、1.
建模预测
在确定了最佳参数后,我们可以进行后续的建模与预测。预测主要有两个函数,一个是predict函数,一个是forecast函数,predict的起始时间必须在原始的数据中的,而forecast则是对训练数据集末尾下一个时间段的值进行预估。
model = ARIMA(data, (0,1,1)).fit() #建立ARIMA(0, 1, 1)模型
model.forecast(5) #作为期5天的预测
这样我们就得到了未来五天的预测数据。之后我们也可以通过实际值和预测值的对比对模型进行调整和进一步的优化
↓↓↓欢迎关注我的公众号,在这里有数据相关技术经验的优质原创文章↓↓↓
![]()