LESSON 12.7 梯度提升树的参数空间与TPE优化

三 GBDT的参数空间与超参数优化

1 确定GBDT优化的参数空间

丰富的超参数为集成算法提供了无限的可能，以降低偏差为目的的Boosting算法们在调参之后的表现更是所向披靡，因此GBDT的超参数自动优化也是一个重要的课题。对任意集成算法进行超参数优化之前，我们需要明确两个基本事实：

1、不同参数对算法结果的影响力大小

2、确定用于搜索的参数空间

对GBDT来说，我们可以大致如下排列各个参数对算法的影响：

如果你熟悉随机森林的超参数，你会发现GBDT中大部分超参数的影响力等级都非常容易理解。树的集成模型们大多拥有相似的超参数，例如抗过拟合、用来剪枝的参数群（max_depth、min_samples_split等），又比如对样本/特征进行抽样的参数们（subsample，max_features等），这些超参数在不同的集成模型中以相似的方式影响模型，因此原则上来说，对随机森林影响较大的参数对GBDT也会有较大的影响。

然而你可能注意到，在随机森林中非常关键的max_depth在GBDT中没有什么地位，取而代之的是Boosting中特有的迭代参数学习率learning_rate。在随机森林中，我们总是在意模型复杂度(max_depth)与模型整体学习能力(n_estimators)的平衡，单一弱评估器的复杂度越大，单一弱评估器对模型的整体贡献就越大，因此需要的树数量就越少。在Boosting算法当中，单一弱评估器对整体算法的贡献由学习率参数learning_rate控制，代替了弱评估器复杂度的地位，因此Boosting算法中我们寻找的是learning_rate与n_estimators的平衡。同时，Boosting算法天生就假设单一弱评估器的能力很弱，参数max_depth的默认值也往往较小（在GBDT中max_depth的默认值是3），因此我们无法靠降低max_depth的值来大规模降低模型复杂度，更难以靠max_depth来控制过拟合，自然max_depth的影响力就变小了。

可见，虽然树的集成算法们大多共享相同的超参数，都由于不同算法构建时的原理假设不同，相同参数在不同算法中的默认值可能被设置得不同，因此相同参数在不同算法中的重要性和调参思路也不同。

在讲解随机森林时我们提到过，精剪枝工具的效用有限，剪枝一般还是大刀阔斧的粗剪枝更有效。在GBDT中，由于max_depth这一粗剪枝工具的默认值为3，因此在Boosting算法中通过削减模型复杂度来控制过拟合的思路就无法走通。特别地，参数init对GBDT的影响很大，如果在参数init中填入具体的算法，过拟合可能会变得更加严重，因此我们需要在抑制过拟合、控制复杂度这一点上令下功夫。

如果无法对弱评估器进行剪枝，最好的控制过拟合的方法就是增加随机性/多样性，因此max_features和subsample就成为Boosting算法中控制过拟合的核心武器，这也是GBDT中会加入Bagging思想的关键原因之一。依赖于随机性、而非弱评估器结构来对抗过拟合的特点，让Boosting算法获得了一个意外的优势：比起Bagging，Boosting更加擅长处理小样本高维度的数据，因为Bagging数据很容易在小样本数据集上过拟合。

需要注意的是，虽然max_depth在控制过拟合上的贡献不大，但是我们在调参时依然需要保留这个参数。当我们使用参数max_features与subsample构建随机性、并加大每一棵树之间的差异后，模型的学习能力可能受到影响，因此我们可能需要提升单一弱评估器的复杂度。因此在GBDT当中，max_depth的调参方向是放大/加深，以探究模型是否需要更高的单一评估器复杂度。相对的在随机森林当中，max_depth的调参方向是缩小/剪枝，用以缓解过拟合。

那在调参的时候，我们应该选择哪些参数呢？与随机森林一样，我们首先会考虑所有影响力巨大的参数（5星参数），当算力足够/优化算法运行较快的时候，我们可以考虑将大部分时候具有影响力的参数（4星）也都加入参数空间，如果样本量较小，我们可能不选择subsample。除此之外，我们还需要部分影响弱评估器复杂度的参数，例如max_depth。如果算力充足，我们还可以加入criterion这样或许会有效的参数。在这样的基本思想下，考虑到硬件与运行时间因素，我将选择如下参数进行调整，并使用基于TPE贝叶斯优化（HyperOpt）对GBDT进行优化——

在此基础上，我们需要进一步确认参数空间。幸运的是，GBDT的参数空间几乎不依赖于树的真实结构进行调整，且大部分参数都有固定的范围，因此我们只需要对无界的参数稍稍探索即可。

其中，我们在《二 4 袋外数据》部分已经对n_estimators进行过探索（如果你没有经过这个探索，则需要绘制绘制学习曲线进行探索），在当前默认参数下，我们大约只需要50次迭代就能够让损失函数收敛，因此我们可以就50这个数字向两侧展开来设置n_estimators的搜索范围。

另外，原则上来说需要用Tree对象来探索min_impurity_decrease的值，但由于我们这个参数只能放大、不能缩小，且我们知道精剪枝对于GBDT的影响较小，因此就不必大费周章地给与该参数一个精细的范围了，按照(0,C)结构走即可，其中C为任意常数。

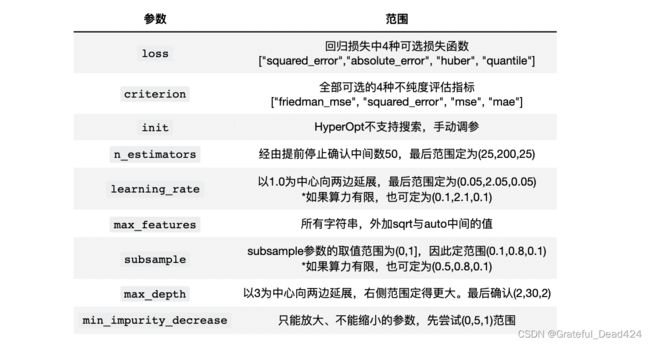
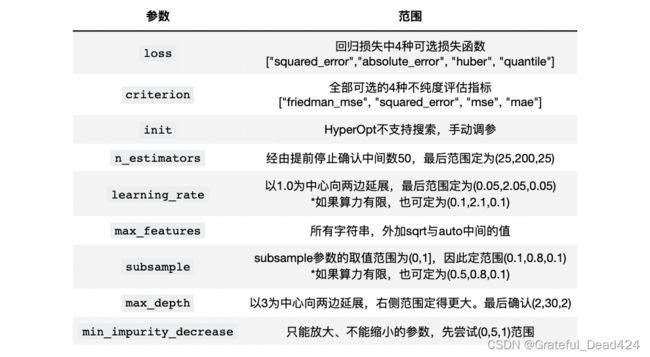
具体每个参数的初始范围确定如下：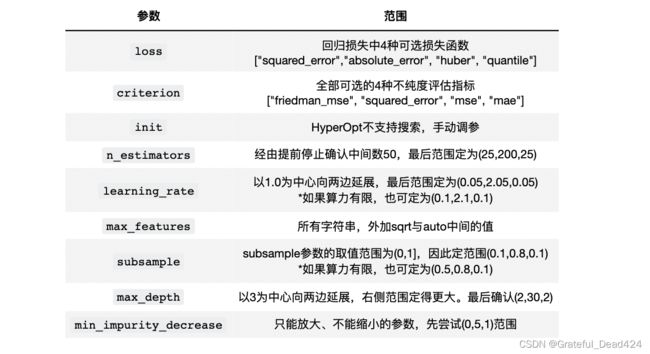
一般在初次搜索时，我们会设置范围较大、较为稀疏的参数空间，然后在多次搜索中逐渐缩小范围、降低参数空间的维度。需要注意的是，init参数中需要输入的评估器对象无法被HyperOpt库识别，因此参数init我们只能手动调参。在之前的课程《二 1.1 初始预测结果H0的设置》中，我们已经对init尝试过三种参数，分别是精调后的模型rf，字符串"zero"与"None"，并且我们已经看到rf给出的结果是最好的，因此我们就按照init= rf来设置参数，不再对该参数进行调整。

2 基于TPE对GBDT进行优化

#日常使用库与算法
import pandas as pd
import numpy as np
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import time
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.model_selection import cross_validate, KFold

#导入优化算法
import hyperopt
from hyperopt import hp, fmin, tpe, Trials, partial
from hyperopt.early_stop import no_progress_loss

data = pd.read_csv("/Users/zhucan/Desktop/train_encode.csv",index_col=0)
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
X.shape
#(1460, 80)

Step 1.建立benchmark

Step 2.定义参数init需要的算法

rf = RFR(n_estimators=89, max_depth=22, max_features=14,min_impurity_decrease=0
         ,random_state=1412, verbose=False, n_jobs=-1)

Step 3.定义目标函数、参数空间、优化函数、验证函数

目标函数

def hyperopt_objective(params):
    reg = GBR(n_estimators = int(params["n_estimators"])
              ,learning_rate = params["lr"]
              ,criterion = params["criterion"]
              ,loss = params["loss"]
              ,max_depth = int(params["max_depth"])
              ,max_features = params["max_features"]
              ,subsample = params["subsample"]
              ,min_impurity_decrease = params["min_impurity_decrease"]
              ,init = rf
              ,random_state=1412
              ,verbose=False)
    
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                     ,error_score='raise'
                                    )
    return np.mean(abs(validation_loss["test_score"]))

参数空间

param_grid_simple = {'n_estimators': hp.quniform("n_estimators",25,200,25)
                  ,"lr": hp.quniform("learning_rate",0.05,2.05,0.05)
                  ,"criterion": hp.choice("criterion",["friedman_mse", "squared_error", "mse", "mae"])
                  ,"loss":hp.choice("loss",["squared_error","absolute_error", "huber", "quantile"])
                  ,"max_depth": hp.quniform("max_depth",2,30,2)
                  ,"subsample": hp.quniform("subsample",0.1,0.8,0.1)
                  ,"max_features": hp.choice("max_features",["log2","sqrt",16,32,64,"auto"])
                  ,"min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,1)
                 }

计算参数空间大小：

len(range(25,200,25)) * len(np.arange(0.05,2.05,0.05)) * 4 * 4 * len(range(2,30,2)) * len(np.arange(0.1,0.8,0.1)) * 6 * len(range(0,5,1))
#13171200

虽然参数分布较为稀疏，但由于参数维度众多、范围较大，因此这是一个超大的参数空间。

优化函数

def param_hyperopt(max_evals=100):
    
    #保存迭代过程
    trials = Trials()
    
    #设置提前停止
    early_stop_fn = no_progress_loss(100)
    
    #定义代理模型
    params_best = fmin(hyperopt_objective
                       , space = param_grid_simple
                       , algo = tpe.suggest
                       , max_evals = max_evals
                       , verbose=True
                       , trials = trials
                       , early_stop_fn = early_stop_fn
                      )
    
    #打印最优参数，fmin会自动打印最佳分数
    print("\n","\n","best params: ", params_best,
          "\n")
    return params_best, trials

验证函数（可选）

def hyperopt_validation(params):    
    reg = GBR(n_estimators = int(params["n_estimators"])
              ,learning_rate = params["learning_rate"]
              ,criterion = params["criterion"]
              ,loss = params["loss"]
              ,max_depth = int(params["max_depth"])
              ,max_features = params["max_features"]
              ,subsample = params["subsample"]
              ,min_impurity_decrease = params["min_impurity_decrease"]
              ,init = rf
              ,random_state=1412 #GBR中的random_state只能够控制特征抽样，不能控制样本抽样
              ,verbose=False)
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                    )
    return np.mean(abs(validation_loss["test_score"]))

#然而对gbdt而言random_state只控制特征随机性不控制样本随机性

Step 4.训练贝叶斯优化器

params_best, trials = param_hyperopt(30) #使用小于0.1%的空间进行训练
#100%|████████████████████████████████████████████████| 30/30 [00:45<00:00,  1.51s/trial, best loss: 26888.311566837725]
 
# best params:  {'criterion': 2, 'learning_rate': 0.2, 'loss': 0, 'max_depth': 24.0, 'max_features': 0, 'min_impurity_decrease': 5.0, 'n_estimators': 175.0, 'subsample': 0.7000000000000001} 

params_best #注意hp.choice返回的结果是索引，而不是具体的数字
#{'criterion': 2,
# 'learning_rate': 0.2,
# 'loss': 0,
# 'max_depth': 24.0,
# 'max_features': 0,
# 'min_impurity_decrease': 5.0,
# 'n_estimators': 175.0,
# 'subsample': 0.7000000000000001}

hyperopt_validation({'criterion': "mse",
                     'learning_rate': 0.2,
                     'loss': "squared_error",
                     'max_depth': 24.0,
                     'max_features': "log2",
                     'min_impurity_decrease': 5.0,
                     'n_estimators': 175.0,
                     'subsample': 0.7})
#26888.311566837725                                   

不难发现，我们已经得到了历史最好分数，但GBDT的潜力远不止如此。现在我们可以根据第一次训练出的结果缩小参数空间，继续进行搜索。在多次搜索中，我发现loss参数的最优选项基本都是平方误差"squared_error"，因此我们可以将该参数排除出搜索队伍。同样，对于其他参数，我们则根据搜索结果修改空间范围、增加空间密度，一般以被选中的值为中心向两边拓展，并减小步长，同时范围可以向我们认为会被选中的一边倾斜。例如最大深度max_depth被选为24，我们则将原本的范围(2,30,2)修改为(10,35,1)。同样subsample被选为0.7，我们则将新范围调整为(0.5,1.0,0.05)，依次类推。

param_grid_simple = {'n_estimators': hp.quniform("n_estimators",150,200,5)
                     ,"lr": hp.quniform("learning_rate",0.05,3,0.05)
                     ,"criterion": hp.choice("criterion",["friedman_mse", "squared_error", "mse","mae"])
                     ,"max_depth": hp.quniform("max_depth",10,35,1)
                     ,"subsample": hp.quniform("subsample",0.5,1,0.05)
                     ,"max_features": hp.quniform("max_features",10,30,1)
                     ,"min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,0.5)
                    }

由于需要修改参数空间，因此目标函数也必须跟着修改：

def hyperopt_objective(params):
    reg = GBR(n_estimators = int(params["n_estimators"])
              ,learning_rate = params["lr"]
              ,criterion = params["criterion"]
              ,max_depth = int(params["max_depth"])
              ,max_features = int(params["max_features"])
              ,subsample = params["subsample"]
              ,min_impurity_decrease = params["min_impurity_decrease"]
              ,loss = "squared_error"
              ,init = rf
              ,random_state=1412
              ,verbose=False)
    
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                     ,error_score='raise'
                                    )
    return np.mean(abs(validation_loss["test_score"]))

params_best, trials = param_hyperopt(30) #使用小于0.1%的空间进行训练
#100%|████████████████████████████████████████████████| 30/30 [00:21<00:00,  1.42trial/s, best loss: 26705.080632614565]
 
# best params:  {'criterion': 2, 'learning_rate': 0.28, 'max_depth': 16.0, 'max_features': 16.0, 'min_impurity_decrease': 3.5, 'n_estimators': 185.0, 'subsample': 0.8500000000000001} 
params_best, trials = param_hyperopt(100) #尝试增加搜索次数
#100%|███████████████████████████████████████████████| 100/100 [05:09<00:00,  3.09s/trial, best loss: 26519.12578332204]
 
# best params:  {'criterion': 2, 'learning_rate': 0.1, 'max_depth': 12.0, 'max_features': 19.0, 'min_impurity_decrease': 0.0, 'n_estimators': 195.0, 'subsample': 0.55} 

基于该结果，我们又可以确定进一步确定部分参数的值（比如criterion），再次缩小参数范围、增加参数空间的密集程度：

def hyperopt_objective(params):
    reg = GBR(n_estimators = int(params["n_estimators"])
              ,learning_rate = params["lr"]
              ,max_depth = int(params["max_depth"])
              ,max_features = int(params["max_features"])
              ,subsample = params["subsample"]
              ,min_impurity_decrease = params["min_impurity_decrease"]
              ,criterion = "mse"
              ,loss = "squared_error"
              ,init = rf
              ,random_state=1412
              ,verbose=False)
    
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                     ,error_score='raise'
                                    )
    return np.mean(abs(validation_loss["test_score"]))

param_grid_simple = {'n_estimators': hp.quniform("n_estimators",175,200,1)
                     ,"lr": hp.quniform("learning_rate",0.1,0.3,0.005)
                     ,"max_depth": hp.quniform("max_depth",8,22,1)
                     ,"subsample": hp.quniform("subsample",0.5,1,0.0025)
                     ,"max_features": hp.quniform("max_features",10,20,1)
                     ,"min_impurity_decrease":hp.quniform("min_impurity_decrease",1,4,0.25)
                    }

params_best, trials = param_hyperopt(300) #缩小参数空间的同时增加迭代次数
# 57%|██████████████████████████▉                    | 172/300 [01:46<01:19,  1.62trial/s, best loss: 26501.91471740881]

# best params:  {'learning_rate': 0.115, 'max_depth': 8.0, 'max_features': 12.0, 'min_impurity_decrease': 2.5, 'n_estimators': 183.0, 'subsample': 1.0} 

def param_hyperopt(max_evals=100):
    
    #保存迭代过程
    trials = Trials()
    
    #设置提前停止
    #early_stop_fn = no_progress_loss(100)
    
    #定义代理模型
    params_best = fmin(hyperopt_objective
                       , space = param_grid_simple
                       , algo = tpe.suggest
                       , max_evals = max_evals
                       , verbose=True
                       , trials = trials
                       #, early_stop_fn = early_stop_fn
                      )
    
    #打印最优参数，fmin会自动打印最佳分数
    print("\n","\n","best params: ", params_best,
          "\n")
    return params_best, trials

params_best, trials = param_hyperopt(300) #取消提前停止，继续迭代
#100%|██████████████████████████████████████████████| 300/300 [03:02<00:00,  1.64trial/s, best loss: 26448.278731971972]

# best params:  {'learning_rate': 0.25, 'max_depth': 9.0, 'max_features': 15.0, 'min_impurity_decrease': 3.25, 'n_estimators': 176.0, 'subsample': 1.0} 

params_best, trials = param_hyperopt(1000)
#100%|████████████████████████████████████████████| 1000/1000 [12:07<00:00,  .38trial/s, best loss: 26415.835015071534]

# best params:  {'learning_rate': 0.21, 'max_depth': 8.0, 'max_features': 13.0, 'min_impurity_decrease': 3.5, 'n_estimators': 187.0, 'subsample': 0.8675} 

start = time.time()
hyperopt_validation({'criterion': "mse",
                     'learning_rate': 0.21,
                     'loss': "squared_error",
                     'max_depth': 8.0,
                     'max_features': 13,
                     'min_impurity_decrease': 3.5,
                     'n_estimators': 187.0,
                     'subsample': 0.8675})
#26415.835015071538          
end = (time.time() - start)
print(end)          
#1.5381402969360352              

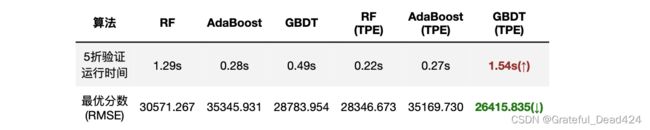
GBDT获得了目前为止的最高分，虽然这一组参数最终指向了187棵树，导致GBDT运行所需的时间远远高于其他算法，GBDT上得到的分数是比精细调参后的随机森林还低2000左右，这证明了GBDT在学习能力上的优越性。由于TPE是带有强随机性的过程，因此如果我们多次运行，我们将得到不同的结果，但GBDT的预测分数可以稳定在26500上下。如果算力支持使用更多的迭代次数、或使用更大更密集的参数空间，我们或许可以得到更好的分数。同时，如果我们能够找到一组大学习率、小迭代次数的参数，那GBDT的训练速度也会随之上升。你可以试着在最初的范围中寻找另一个突破口，尝试将GBDT的速度降低。