DenseNet：密集卷积网络（2018）

[paper]Densely Connected Convolutional Networks(2018)
[code]liuzhuang13/DenseNet
[mxnet code]miraclewkf/DenseNet

文章

摘要

最近的工作表明，如果卷积网络在靠近输入的层和靠近输出的层之间包含更短的连接，则它们可以更深入、更准确、更有效地进行训练。在本文中，我们接受了这一观察并介绍了密集卷积网络 (DenseNet)，它以前馈方式将每一层连接到其他每一层。而具有 L 层的传统卷积网络有 L 个连接——每层与其后续层之间有一个连接——而我们的网络有 $\frac{L(L+1)}{2}$个直接连接。对于每一层，所有先前层的特征图用作输入，其自身的特征图用作所有后续层的输入。DenseNets 有几个引人注目的优点：它们减轻了梯度消失问题，加强了特征传播，鼓励特征重用，并大大减少了参数的数量。我们在四个竞争激烈的对象识别基准任务（CIFAR-10、CIFAR-100、SVHN 和 ImageNet）上评估了我们提出的架构。DenseNets 在大多数情况下获得了比最先进的显着改进，同时需要更少的计算来实现高性能。代码和预训练模型可从 https://github.com/liuzhuang13/DenseNet 获得。

介绍

卷积神经网络 (CNN) 已成为视觉对象识别的主要机器学习方法。尽管它们最初是在 20 多年前推出的 [18]，但直到最近，计算机硬件和网络结构的改进才使真正深度 CNN 的训练成为可能。最初的 LeNet5 [19] 由 5 层组成，VGG 有 19 个 [29]，仅在去年，Highway Networks [34] 和 Residual Networks (ResNets) [11] 超过了 100 层的障碍。

随着 CNN 变得越来越深，一个新的研究问题出现了：当有关输入或梯度的信息经过许多层时，它可能会在到达网络的末尾（或开头）时消失并“洗掉”。许多最近的出版物解决了这个或相关的问题。ResNets [11] 和 Highway Networks [34] 通过身份连接将信号从一层绕过到下一层。随机深度 [13] 通过在训练期间随机丢弃层来缩短 ResNets，以允许更好的信息和梯度流。FractalNets [17] 反复组合多个具有不同卷积块数量的并行层序列，以获得较大的标称深度，同时在网络中保持许多短路径。尽管这些不同的方法在网络拓扑和训练过程上有所不同，但它们都有一个关键特征：它们创建了从早期层到后期层的短路径。

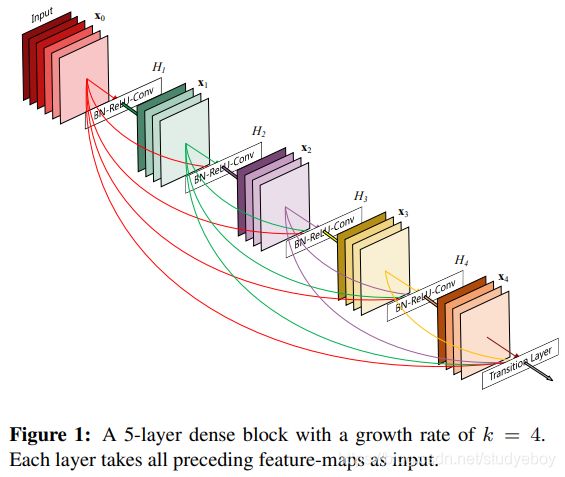
在本文中，我们提出了一种架构，将这种见解提炼为一种简单的连接模式：为了确保网络中各层之间的信息流最大化，我们将所有层（具有匹配的特征图大小）直接相互连接。为了保持前馈特性，每一层从所有前面的层获得额外的输入，并将它自己的特征图传递给所有后续层。图 1 示意性地说明了这种布局。至关重要的是，与 ResNets 相比，我们从不在将特征传递到层之前通过求和来组合特征； 相反，我们通过连接特征来组合特征。因此，第$l^{th}$层有$l$输入，由所有前面卷积块的特征图组成。它自己的特征图被传递到所有 $L-l$后续层。这在 $L$ 层网络中引入了 $\frac{L(L+1)}{2}$ 个连接，而不仅仅是传统架构中的 $L$。由于其密集的连接模式，我们将我们的方法称为密集卷积网络（DenseNet）。

这种密集连接模式的一个可能违反直觉的影响是它需要比传统卷积网络更少的参数，因为不需要重新学习冗余特征图。传统的前馈架构可以被视为具有状态的算法，该状态在层与层之间传递。每一层从其前一层读取状态并将其写入后续层。它会改变状态，但也会传递需要保留的信息。ResNets [11] 通过附加的身份转换使这种信息保存变得明确。ResNets [13] 的最新变化表明，许多层贡献很小，实际上可以在训练期间随机丢弃。 这使得 ResNets 的状态类似于（展开的）循环神经网络 [21]，但 ResNets 的参数数量要大得多，因为每一层都有自己的权重。我们提出的 DenseNet 架构明确区分添加到网络的信息和保留的信息。DenseNet 层非常窄（例如，每层 12 个过滤器），仅将一小组特征映射添加到网络的“集体知识”中并保持其余特征映射不变——最终分类器基于网络中的所有特征图做出决策。

除了更好的参数效率外，DenseNets 的一大优势是改进了整个网络的信息流和梯度，这使得它们易于训练。每一层都可以直接访问来自损失函数和原始输入信号的梯度，从而导致隐式的深度监督 [20]。这有助于训练更深的网络架构。此外，我们还观察到密集连接具有正则化效果，这减少了对具有较小训练集大小的任务的过度拟合。

我们在四个竞争激烈的基准数据集（CIFAR-10、CIFAR-100、SVHN 和 ImageNet）上评估 DenseNets。我们的模型往往需要比具有可比精度的现有算法少得多的参数。此外，我们在大多数基准任务上的表现明显优于当前最先进的结果。

相关工作

自最初发现以来，对网络架构的探索一直是神经网络研究的一部分。最近神经网络的流行回潮也使这一研究领域复苏。现代网络中层数的增加放大了架构之间的差异，并激发了对不同连接模式的探索和对旧研究思想的重新审视。

在 1980 年代的神经网络文献中已经研究了类似于我们提出的密集网络布局的级联结构 [3]。他们的开创性工作侧重于以逐层方式训练的全连接多层感知器。最近，提出了用批量梯度下降训练的全连接级联网络 [40]。尽管对小数据集有效，但这种方法仅适用于具有几百个参数的网络。在 [9, 23, 31, 41] 中，已经发现通过跳过连接在 CNN 中利用多级特征对各种视觉任务是有效的。平行于我们的工作，[1]导出用于与类似于我们跨层网络连接纯理论的框架。

高速公路网络 [34] 是最早提供一种方法来有效训练 100 层以上的端到端网络的架构之一。使用旁路路径和门控单元，可以毫不费力地优化具有数百层的公路网络。绕过路径被认为是简化这些非常深网络的训练的关键因素。ResNets [11] 进一步支持这一点，其中使用纯身份映射作为绕过路径。ResNets 在许多具有挑战性的图像识别、定位和检测任务（例如 ImageNet 和 COCO 对象检测 [11]）上取得了令人印象深刻、破纪录的性能。最近，随机深度被提出作为一种成功训练 1202 层 ResNet [13] 的方法。随机深度通过在训练期间随机丢弃层来改进深度残差网络的训练。这表明并非所有层都需要，并强调深度（残差）网络中存在大量冗余。我们的论文部分受到了这一观察的启发。具有预激活功能的 ResNet 还有助于训练具有 > 1000 层的最先进网络 [12]。使网络更深的正交方法（例如，在跳过连接的帮助下）是增加网络宽度。GoogLeNet [36, 37] 使用“Inception 模块”，该模块连接由不同大小的过滤器生成的特征图。在 [38] 中，提出了一种具有广泛广义残差块的 ResNets 变体。事实上，只要深度足够，简单地增加每层 ResNet 中的过滤器数量就可以提高其性能 [42]。FractalNets 还使用广泛的网络结构在多个数据集上取得了有竞争力的结果 [17]。

DenseNets 不是从极深或极宽的架构中汲取表征能力，而是通过特征重用来利用网络的潜力，产生易于训练且参数效率高的浓缩模型。连接不同层学习的特征图会增加后续层输入的变化并提高效率。这构成了 DenseNets 和 ResNets 之间的主要区别。与也连接来自不同层的特征的 Inception 网络 [36, 37] 相比，DenseNets 更简单、更高效。

还有其他显着的网络架构创新已经产生了有竞争力的结果。网络中的网络 (NIN) [22] 结构将微型多层感知器包含在卷积层的过滤器中，以提取更复杂的特征。在深度监督网络（DSN）[20]中，内部层由辅助分类器直接监督，这可以加强早期层接收到的梯度。梯形网络 [27, 25] 将横向连接引入自动编码器，在半监督学习任务上产生令人印象深刻的准确性。在 [39] 中，提出了深度融合网络 (DFN)，通过组合不同基础网络的中间层来改善信息流。具有最小化重建损失的路径的网络增强也被证明可以改进图像分类模型 [43]。

DenseNets

考虑通过卷积网络的单个图像 $x_0$。该网络由 $L$ 层组成，每一层都实现了一个非线性变换 $H_l(\cdot )$，其中$l$为该层索引。$H_l(\cdot )$可以是诸如批量归一化 (BN) [14]、整流线性单元 (ReLU) [6]、池化 [19] 或卷积 (Conv) 等操作的复合函数。 我们将第$l^{th}$层的输出表示为 $x_l$。

ResNets. 传统的卷积前馈网络将第$l^{th}$层的输出作为输入连接到第$(l+1{)}^{th}$层[16]，从而产生以下层转换：$x_l=H_l(x_{l-1})$。ResNets [11] 添加了一个跳过连接，使用恒等函数绕过非线性变换：

ResNets 的一个优点是梯度可以直接通过恒等函数从后面的层流到前面的层。然而，恒等函数和$H_l$的输出是通过求和组合的，这可能会阻碍网络中的信息流动。
Dense connectivity 为了进一步改善层之间的信息流，我们提出了一种不同的连接模式：我们引入了从任何层到所有后续层的直接连接。图 1 示意性地说明了生成的 DenseNet 的布局。因此，$l^{th}$ 层接收所有前面层的特征图，$x_0，...,x_{l-1}$, 作为输入：

其中$[x_0,x_1,...,x_{l-1}]$ 是指在层 $0,...,l-1$ 中生成的特征图的串联。由于其密集的连接性，我们将这种网络架构称为密集卷积网络 (DenseNet)。为了便于实现，我们将等式 (2)中 $H_l(\cdot )$ 的多个输入连接起来成单个张量。

Composite function 受 [12] 的启发，我们将 $H_l(\cdot )$ 定义为三个连续操作的复合函数：批量归一化 (BN) [14]，然后是整流线性单元 (ReLU) [6] 和 3 × 3 卷积（ 转化）。

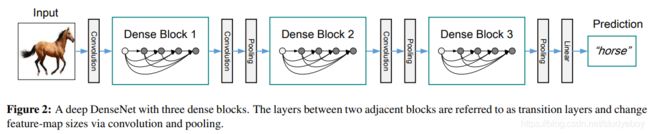
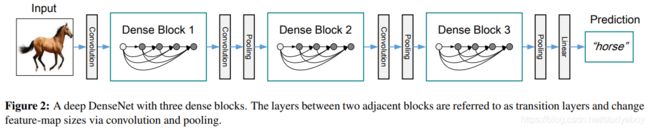
Pooling layers等式(2)中使用的连接操作，当特征图的大小改变时是不可行的。然而，卷积网络的一个重要部分是改变特征图大小的下采样层。为了在我们的架构中进行下采样，我们将网络划分为多个密集连接的密集块； 见图 2。我们将块之间的层称为过渡层，它们进行卷积和池化。我们实验中使用的过渡层由一个批量归一化层和一个 1×1 卷积层和一个 2×2 平均池化层组成。

Growth rate如果每个函数 $H_l$产生 $k$ 个特征图，那么第$l^{th}$层有 $k_0+k\times (l-1)$个输入特征图，其中 $k_0$ 是输入层中的通道数。DenseNet 和现有网络架构之间的一个重要区别是 DenseNet 可以具有非常窄的层，例如，$k=12$。我们将超参数 $k$ 称为网络的增长率。我们在第 4 节中表明，相对较小的增长率足以在我们测试的数据集上获得最先进的结果。对此的一个解释是，每一层都有访问在块中的所有前面的特征图，因此，网络上的“集体智慧”。人们可以将特征图视为网络的全局状态。每个层都将自己的 $k$ 个特征图添加到这个状态。增长率调节每层对全局状态贡献多少新信息。全局状态一旦写入，就可以从网络内的任何地方访问，并且与传统网络架构不同，不需要在层与层之间复制它。

Bottleneck layers虽然每一层只产生$k$个输出特征图，但它通常有更多的输入。在 [37, 11] 中已经注意到，可以在每个 3×3 卷积之前引入 1×1 卷积作为瓶颈层，以减少输入特征图的数量，从而提高计算效率。我们发现这种设计对 DenseNet 特别有效，我们将我们的网络称为具有这样一个瓶颈层的网络，即 $H_l$ 的 BN-ReLU-Conv(1×1)-BN-ReLU-Conv(3×3) 版本， 作为 DenseNet-B。在我们的实验中，我们让每个 1×1 卷积产生 $4k$ 个特征图。

Compression为了进一步提高模型的紧凑性，我们可以减少过渡层的特征图数量。如果一个密集块包含 $m$ 个特征图，我们让下面的过渡层生成 $\lfloor \theta m\rfloor$ 输出特征图，其中 $0<\theta \le 1$ 被称为压缩因子。当 $\theta =1$ 时，跨过渡层的特征图数量保持不变。我们将 $\theta <1$ 的 DenseNet 称为 DenseNet-C，我们在实验中设置 $\theta =0.5$。当同时使用 $\theta <1$ 的瓶颈层和过渡层时，我们将我们的模型称为 DenseNet-BC。

Implementation Details在除 ImageNet 之外的所有数据集上，我们实验中使用的 DenseNet 具有三个密集块，每个块都有相同的层数。在进入第一个密集块之前，对输入图像执行具有 16 个（或 DenseNet-BC 增长率的两倍）输出通道的卷积。对于内核大小为 3×3 的卷积层，输入的每一侧都用一个像素进行零填充，以保持特征图大小固定。我们使用 1×1 卷积，然后是 2×2 平均池化作为两个连续密集块之间的过渡层。在最后一个密集块的末尾，执行全局平均池化，然后附加一个 softmax 分类器。三个密集块中的特征图大小分别为 32×32、16×16 和 8×8。我们用配置 {L = 40, k = 12}、{L = 100, k = 12} 和 {L = 100, k = 24} 对基本的 DenseNet 结构进行实验。对于 DenseNet-BC，评估配置为 {L = 100, k = 12}、{L= 250, k= 24} 和 {L= 190, k= 40} 的网络。

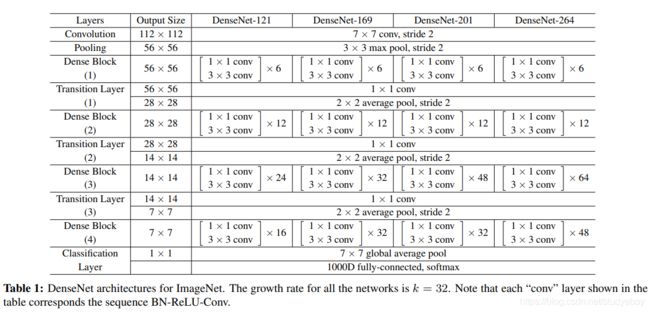
在我们对 ImageNet 的实验中，我们在 224×224 输入图像上使用具有 4 个密集块的 DenseNet-BC 结构。初始卷积层包含 $2k$个大小为 7×7、步幅为 2 的卷积； 所有其他层中的特征图数量也来自设置 $k$。我们在 ImageNet 上使用的确切网络配置如表 1 所示。

实验

我们凭经验证明了 DenseNet 在几个基准数据集上的有效性，并与最先进的架构进行了比较，尤其是与 ResNet 及其变体。

数据集

CIFAR两个 CIFAR 数据集 [15] 由 32×32 像素的彩色自然图像组成。CIFAR-10 (C10) 由来自 10 个类别的图像和来自 100 个类别的 CIFAR-100 (C100) 组成。训练集和测试集分别包含 50,000 和 10,000 张图像，我们保留 5,000 张训练图像作为验证集。我们采用广泛用于这两个数据集的标准数据增强方案（镜像/移位）[11、13、17、22、28、20、32、34]。我们在数据集名称（例如，C10+）的末尾用“+”标记表示这个数据增强方案。对于预处理，我们使用通道均值和标准差对数据进行归一化。对于最终运行，我们使用所有 50,000 张训练图像并在训练结束时报告最终测试错误。

SVHN街景房屋号码 (SVHN) 数据集 [24] 包含 32×32 彩色数字图像。训练集中有 73,257 张图像，测试集中有 26,032 张图像，还有 531,131 张用于额外训练的图像。按照惯例 [7, 13, 20, 22, 30] 我们使用所有训练数据而不进行任何数据增强，并将包含 6,000 张图像的验证集从训练集中拆分。我们在训练期间选择验证错误最低的模型并报告测试错误。我们遵循 [42] 并将像素值除以 255，使它们在 [0, 1] 范围内。

ImageNetILSVRC 2012 分类数据集 [2] 包含来自 1,000 个类别的 120 万张用于训练的图像和 50,000 张用于验证的图像。我们采用与 [8, 11, 12] 中相同的数据增强方案来训练图像，并在测试时应用大小为 224×224 的单次或 10 次裁剪。 遵循 [11, 12, 13]，我们报告了验证集的分类错误。

训练

所有网络都使用随机梯度下降 (SGD) 进行训练。在 CIFAR 和 SVHN 上，我们分别使用批量大小 64 进行 300 和 40 轮训练。初始学习率设置为 0.1，并在训练 epoch 总数的 50% 和 75% 处除以 10。在 ImageNet 上，我们以 256 的批量大小训练了 90 个时期的模型。学习率最初设置为 0.1，并在 30 和 60 时期降低 10 倍。请注意，DenseNet 的简单实现可能包含内存效率低下的问题。为了减少 GPU 上的内存消耗，请参阅我们关于 DenseNets [26] 内存高效实现的技术报告。

遵循 [8]，我们使用 $10^{-4}$ 的权重衰减和 0.9 的 Nesterov 动量 [35] 没有阻尼。我们采用[10]引入的权重初始化。对于没有数据增强的三个数据集，即 C10、C100 和 SVHN，我们在每个卷积层（第一个除外）之后添加一个 dropout 层 [33]，并将 dropout 率设置为 0.2。对于每个任务和模型设置，测试错误仅评估一次。

CIFAR 和 SVHN 的分类结果

我们训练具有不同深度 $L$ 和增长率 $k$ 的 DenseNets。在 CIFAR 和 SVHN 上的主要结果如表 2 所示。为了突出总体趋势，我们将所有优于现有最先进技术的结果用黑体标记，将总体最佳结果标记为蓝色。

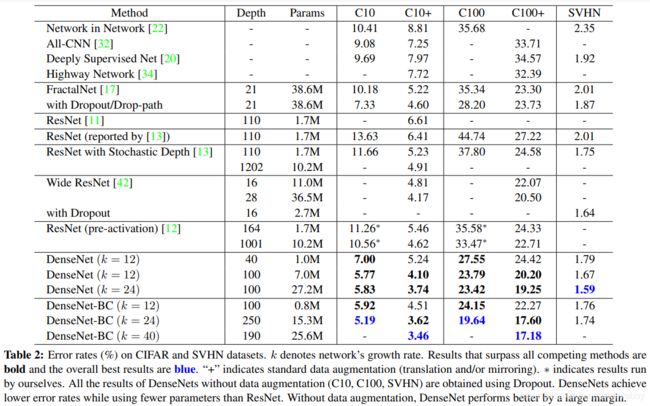
Accuracy可能最明显的趋势可能来自表 2 的底行，这表明 L = 190 和 k = 40 的 DenseNet-BC 在所有 CIFAR 数据集上始终优于现有的最新技术。它在 C10+ 上的错误率为 3.46%，在 C100+ 上为 17.18%，明显低于宽 ResNet 架构 [42] 所达到的错误率。我们在 C10 和 C100（没有数据增强）上的最佳结果更加令人鼓舞：两者都比使用 drop-path 正则化的 FractalNet 低近 30% [17]。在 SVHN 上，使用 dropout，L = 100 和 k = 24 的 DenseNet 也超过了宽 ResNet 实现的当前最佳结果。然而，与较短的对应物相比，250 层 DenseNet-BC 并没有进一步提高性能。这可能是因为 SVHN 是一项相对容易的任务，极深的模型可能会过度拟合训练集。

Capacity如果没有压缩或瓶颈层，DenseNets 会随着 $L$ 和 $k$ 的增加而表现得更好。我们将这主要归因于模型容量的相应增长。C10+ 和 C100+ 列最好地证明了这一点。在 C10+ 上，随着参数数量从 1.0M、超过 7.0M 增加到 27.2M，误差从 5.24% 下降到 4.10%，最终下降到 3.74%。在 C100+ 上，我们观察到类似的趋势。这表明 DenseNets 可以利用更大更深模型的增强表示能力。它还表明它们没有过拟合或残差网络的优化困难 [11]。

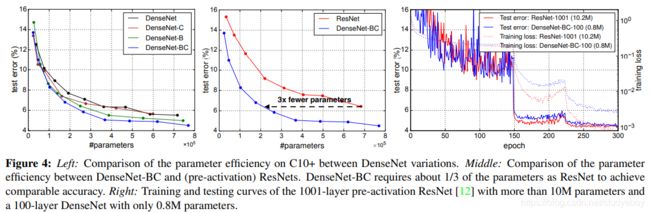
Parameter Efficiency表 2 中的结果表明 DenseNets 比替代架构（特别是 ResNets）更有效地利用参数。在过渡层具有瓶颈结构和降维的 DenseNet-BC 参数效率特别高。例如，我们的 250 层模型只有 1530 万个参数，但它始终优于其他模型，例如 FractalNet 和 Wide ResNets 等参数超过 30M 的模型。我们还强调，L=100和k=12的DenseNet BC与1001层预激活ResNet相比，使用更少90%的参数，可获得相当的性能（例如，C10+上的误差为4.51%对4.62%，C100+上的误差为22.27%对22.71%）。图 4（右图）显示了这两个网络在 C10+ 上的训练损失和测试误差。 1001 层深度 ResNet 收敛到较低的训练损失值，但具有类似的测试错误。 我们将在下面更详细地分析这种影响。

Overfitting更有效地使用参数的一个积极副作用是 DenseNets 不太容易过度拟合。我们观察到，在没有数据增强的数据集上，DenseNet 架构相对于先前工作的改进特别明显。在 C10 上，改进表示错误相对减少了 29%，从 7.33% 减少到 5.19%。在 C100 上，减少约 30%，从 28.20% 到 19.64%。在我们的实验中，我们观察到在单个设置中潜在的过度拟合：在 C10 上，通过将 k = 12 增加到 k = 24 产生的参数增长 4 倍导致误差从 5.77% 适度增加到 5.83%。DenseNet-BC 瓶颈和压缩层似乎是应对这一趋势的有效方法。

ImageNet 上的分类结果

我们在 ImageNet 分类任务上评估具有不同深度和增长率的 DenseNet-BC，并将其与最先进的 ResNet 架构进行比较。为了确保两种架构之间的公平比较，我们通过采用 [8] 1 的 ResNet 公开可用 Torch 实现来消除所有其他因素，例如数据预处理和优化设置的差异。我们简单地用 DenseNetBC 网络替换 ResNet 模型，并保持所有实验设置与用于 ResNet 的完全相同。

我们在表 3 中报告了 ImageNet 上 DenseNets 的单次和 10 次验证错误。图 3 显示了作为参数数量（左）和 FLOP（右）数量的函数的 DenseNets 和 ResNets 的单次裁剪 top-1 验证错误。图中显示的结果表明，DenseNets 的性能与最先进的 ResNets 相当，同时需要更少的参数和计算来实现可比的性能。例如，具有 20M 参数的 DenseNet-201 模型产生与具有超过 40M 参数的 101 层 ResNet 类似的验证错误。从右侧面板可以观察到类似的趋势，该面板将验证误差绘制为 FLOP 数量的函数：需要与 ResNet-50 一样多的计算的 DenseNet 与需要两倍的 ResNet-101 执行相同计算。

值得注意的是，我们的实验设置意味着我们使用针对 ResNet 而非 DenseNet 优化的超参数设置。可以想象，更广泛的超参数搜索可能会进一步提高 DenseNet 在 ImageNet 上的性能。然而，这种看似很小的修改的含义导致两种网络架构的行为截然不同。

讨论

从表面上看，DenseNets 与 ResNets 非常相似：等式(2) 不同于等式 (1) 仅在于 $H_l(\cdot )$ 的输入被连接而不是求和。

Model compactness作为输入连接的直接结果，任何 DenseNet 层学习的特征图都可以被所有后续层访问。这鼓励在整个网络中重用特征，并导致更紧凑的模型。

图 4 中左侧的两个图显示了一个实验的结果，该实验旨在比较 DenseNets（左）和可比较的 ResNet 架构（中）的所有变体的参数效率。我们在 C10+ 上训练多个不同深度的小型网络，并将它们的测试精度绘制为网络参数的函数。与其他流行的网络架构（例如 AlexNet [16] 或 VGG-net [29]）相比，具有预激活功能的 ResNet 使用更少的参数，同时通常会获得更好的结果 [12]。因此，我们将 DenseNet (k = 12) 与此架构进行比较。DenseNet 的训练设置与上一节保持相同。

该图显示 DenseNet-BC 始终是 DenseNet 参数效率最高的变体。此外，为了达到相同的精度水平，DenseNet-BC 只需要 ResNets 参数的 1/3 左右（中间图）。这个结果与我们在图 3 中展示的 ImageNet 上的结果一致。图 4 中的右图显示，只有 0.8M 可训练参数的 DenseNet-BC 能够达到与具有 10.2M 参数的 1001 层（预激活）ResNet [12] 相当的精度。

Implicit Deep Supervision密集卷积网络精度提高的一种解释可能是单个层通过较短的连接从损失函数接收额外的监督。人们可以将 DenseNets 解释为执行一种“深度监督”。深度监督的好处之前已经在深度监督网络 (DSN; [20]) 中得到证明，该网络在每个隐藏层都有分类器，强制中间层学习判别特征。

DenseNets 以隐式方式执行类似的深度监督：网络顶部的单个分类器通过最多两个或三个转换层为所有层提供直接监督。然而，DenseNets 的损失函数和梯度要简单得多，因为所有层之间共享相同的损失函数。

随机与确定性连接密集卷积网络和残差网络的随机深度正则化之间存在有趣的联系 [13]。在随机深度中，残差网络中的层被随机丢弃，这在周围层之间创建了直接连接。由于池化层永远不会被丢弃，因此网络会产生与 DenseNet 类似的连接模式：如果所有中间层都被随机丢弃，则同一池化层之间的任何两层直接连接的可能性很小。尽管方法最终完全不同，但 DenseNet 对随机深度的解释可能会提供有关此正则化器成功的见解。

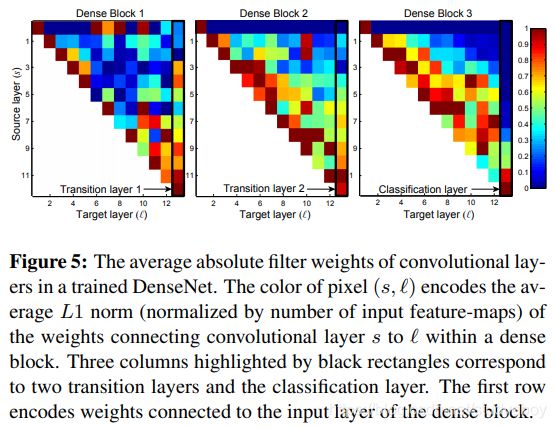
Feature Reuse通过设计，DenseNets 允许层从其所有前面的层（尽管有时通过过渡层）访问特征图。我们进行了一项实验，以调查训练有素的网络是否利用了这个机会。我们首先在 L = 40 和 k = 12 的 C10+ 上训练 DenseNet。对于块内的每个卷积层$l$，我们计算分配给与层 $s$ 的连接的平均（绝对）权重。 图 5 显示了所有三个密集块的热图。平均绝对权重用作卷积层对其前一层的依赖性的替代。位置 $(l,s)$ 处的红点表示层$l$平均而言，强烈使用了之前生成的 $s$ 层的特征图。从图中可以得出几个观察结果：

• 所有层将它们的权重分布在同一块内的许多输入上。 这表明由非常早的层提取的特征确实直接被整个同一个密集块中的深层使用。
• 过渡层的权重也将它们的权重分散到前一个密集块内的所有层，表明信息从 DenseNet 的第一层到最后一层通过很少的间接方式流动。
• 第二个和第三个密集块中的层始终为过渡层的输出（三角形的顶行）分配最小的权重，表明过渡层输出了许多冗余特征（平均权重较低）。 这与 DenseNet-BC 的强大结果一致，其中这些输出被压缩。
• 尽管最右边显示的最终分类层也使用整个密集块的权重，但似乎集中在最终特征图上，这表明可能在网络后期产生了一些更高级的特征。
  

结论

我们提出了一种新的卷积网络架构，我们将其称为密集卷积网络 (DenseNet)。它引入了具有相同特征图大小的任意两层之间的直接连接。我们展示了 DenseNets 自然地扩展到数百层，同时没有表现出优化困难。在我们的实验中，DenseNets 倾向于随着参数数量的增加而不断提高准确性，而没有任何性能下降或过度拟合的迹象。在多种设置下，它在多个竞争激烈的数据集上取得了最先进的结果。此外，DenseNets 需要更少的参数和更少的计算来实现最先进的性能。由于我们在研究中采用了针对残差网络优化的超参数设置，因此我们相信可以通过更详细地调整超参数和学习率计划来进一步提高 DenseNets 的准确性。

在遵循简单的连接规则的同时，DenseNets 自然地集成了身份映射、深度监督和多样化深度的特性。它们允许在整个网络中重用特征，因此可以学习更紧凑，根据我们的实验，更准确的模型。由于其紧凑的内部表示和减少的特征冗余，DenseNets 可能是各种基于卷积特征的计算机视觉任务的良好特征提取器，例如 [4, 5]。我们计划在未来的工作中使用 DenseNets 研究这种特征转移。

文章解读

DenseNet(密集卷积网络)主要还是和ResNet及Inception网络做对比，思想上有借鉴，但却是全新的结构。卷积神经网络提高效果的方向，要么深（比如ResNet，解决了网络深时候的梯度消失问题），要么宽（比如GoogLeNet），而作者从功能入手，通过对功能的极致利用达到更好的效果和更少的参数。DenseNet减轻了消失梯度，加强了特征的传递，更有效的利用了特征，一定程度上减少了参数数量。在保证网络中层与层之间最大程度的信息传输的前提下，直接将所有层连接起来。

Dense Block

在传统的卷积神经网络中，如果有L层，那么就会有L个连接，但是在DenseNet中，会有L(L+1)/2个连接，即每一层的输入来自前面所有层的输出。如下图所示，$x_0$是输入，$H_1$的输入是$x_0$（输入），$H_2$的输入是$x_0$和$x_1$（$x_1$是$H_1$的输出），依次类推。

网络结构

在这个结构网络中包含了3个dense block。作者将DenseNet分成多个dense block，希望各个dense block内的feature map的size统一，这样在做concatenation就不会有size问题。

• DenseNet和ResNet的区别

  • ResNet
    $l$表示层，$x_l$表示$l$层的输出，$H_l$表示一个非线性变换。所以对ResNet而言，$l$层的输出是$l-1$层的输出加上对$l-1$层的输出的非线性变换。
    
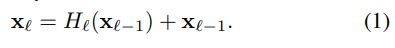
  • DenseNet
    $[x_0,x_1,x_2,...x_{l-1}]$表示将0到$l-1$层的输出feature map做concatenation。concatenation是做通道的合并，就行Inception那样，而ResNet做值的相加，通道数是不变的，$H_l$包括BN、ReLU和3x3的卷积。
    

• 紧密连接（Dense connectivity）
  在Dense结构中，将每一层的输出都导入后面的所有层，与ResNet的相加不同的是，DenseNet结构使用的是连接结构（concatenate）。这样的结构可以减少网络参数，避免ResNet中可能出现的缺点（例如某些层被选择性丢弃，信息阻塞等）。

• 组成函数（Composite function）
  Batch Normalization + ReLU + 3x3 Conv层

• 过渡层（Transition Layer）
  过渡层包含瓶颈层（bottleneck layer，即1x1卷积层）和池化层。

  • 瓶颈层
    1x1的卷积层用于压缩参数。每一层输出$k$个feature maps，理论上将每个Dense Block输出为$4k$个feature maps，然而实际情况会大于这个数字。卷积层的作用是将一个DenseBlock的参数压缩到$4k$个。
  • 池化层
    由于采用了Dense Connectivity结构，直接在各个层之间加入池化层是不可行的，因此采用的是DenseBlock组合的方式，在各个Dense Block之间加入卷积层和池化层。

• 增长率（Growth rate）
  增长率代表的是每一层输出的feature maps的厚度。ResNet，GoogLeNet等网络结构中经常能见到输出厚度为上百个，其目的主要是为了提取不同的特征。但是由于DenseNet中每一层都能直接为后面的网络所用，所以$k$被限制在一个很小的数值。

• 压缩（Compression）
  跟1x1卷积层做用类似，压缩参数。作者选择压缩率为0.5。包含Bottleneck layer的叫作DenseNet-B，包含压缩层的较DenseNet-C，两者都包含的较DenseNet-BC。

在该表中$k=32$是growth rate，表示每个dense block中每层输出的feature map个数。为了避免网络变得很宽，作者都是采用较小的$k$，且较小的$k$可以有更好的效果。根据dense block的设计，后面几层可以得到前面所有层的输入，因此concat后的输入channel还是比较大的。另外这里每个dense block的3x3卷积前面都包含了一个1x1的卷积操作，就是所谓的Bottleneck layer，目的是减少输入的feature map数量，既能降维减少计算量，又能融合各个通道的特征。另外为了进一步压缩参数，在每两个dense block之间又增加了1x1的卷积操作。因此在后面的实验对比中，DenseNet-C就表示增加了这个Transition layer，该层的1x1卷积的输出channel默认是输入channel到一半。DenseNet-BC表示既有bottleneck layer又有transition layer。

在每个Dense Block中都包含很多个子结构，以DenseNet-169的Dense Block（3）为例，包含32个1x1和3x3的卷积操作，也就是第32个子结构的输入是前面31层的输出结果，每层输出的channel是32（growth rate），那么如果不做Bottleneck操作，第32层的3x3卷积操作的输入就是31*32+（上一个Dense Block的输出channel），近1000了。而加上1x1的卷积，代码中的1x1卷积的channel是growth rate * 4，也就是128，然后在作为3x3卷积的输入。这就大大减少了计算量，这就是Bottleneck。至于transition layer，放在两个Dense Block中间，是因为每个Dense Block结束后的输出channel个数很多，需要用1x1的卷积核来降维。还是以DenseNet-169的Dense Block（3）为例，虽然第32层的3x3卷积输出channel只有32个（growth rate），但是紧接着还会像前面几层一样有通道的concate操作，即将第32层的输出和第32层的输入做concat，前面说过第32层的输入是1000左右的channel，所以最后每个Dense Block的输出也是1000多的channel。因此这个transition layer有个参数reduction（范围是0到1），表示将这些输出缩小到原来的多少被，默认是0.5，这样传给下一个Dense Block的时候channel数量就会减少一半，这就是transition layer的作用。文中还用到dropout操作来随机减少分支，避免过拟合，毕竟连接确实多。

该表格是在三个数据集（C10， C100， SVHN）上和其他算法的对表结果。DenseNet-BC的网络参数和相同深度的DenseNet相比确实减少了很多，参数减少除了可以节省内存，还能减少过拟合。在表格的倒数第二个区域的三个不同深度$L$和$k$的DenseNet的对比可以看出随着$L$和$k$的增加，模型的效果是更好的。

DenseNet-BC和ResNet在Imagenet数据集上对对比，左图是参数复杂度和错误率的对比，可以在相同错误率下看参数复杂度，也可以在相同参数复杂度下看错误率，提升还是很明显的。右边可以理解为计算复杂度和错误率的对比，同样有效果。

左图表示不同类型DenseNet的参数和error对比。中间的图表示DenseNet-BC和ResNet的对比，相同error下，DenseN-BC的参数复杂度要小很多。右图也是表达DenseNet-BC-100只需要很少的参数就能达到和ResNet-1001相同的结果。

DenseNet和随机深度的关系，在随机深度中，ResNet中的层在训练过程中会被随机掉，其实这就会使得相邻层之间直接连接，这和DenseNet很像。

参考资料
DenseNet算法详解