【PCA实现与实战】基于python实现PCA算法并用于手写数字识别
PCA算法是机器学习与深度学习中很常见的一种算法, 近期看花书的时候看到了这个算法,所以在写完理论之后也想通过一些实例来帮助理解PCA。
关于PCA算法的理论部分可以查看大佬的文章
以下是基于python自己实现的PCA算法并使用了Kaggle平台的手写数字数据集,
- 官方下载链接:https://www.kaggle.com/c/digit-recognizer/data
- 百度云链接:https://download.csdn.net/download/weixin_43776305/19160516
python实现PCA
PAC步骤
- 原数据D
- 去中心化D’ = D - D^
- 求协方差矩阵C = np.cov(D’)
- 求C的特征值和特征向量
- 特征值从大到小排列取前k个
- 取这k个特征值对应的特征向量构成P
- 降维后的数据Y = D’P
二维数据可视化
- 随机产生
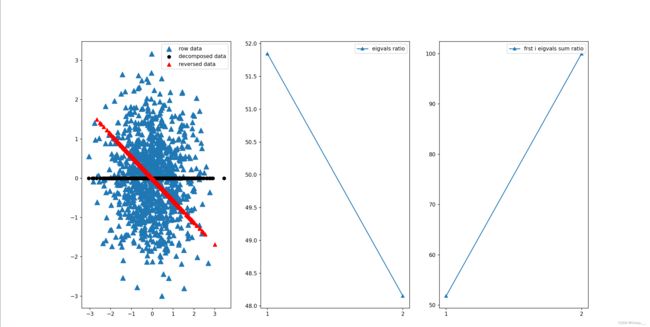
m条2维数据 pca得到四个结果:压缩后的数据、还原后的数据、每个特征值所占的比例、前i个特征值的和所占的比例- 可视化
def load_data(path=None, m=10000):
if not path:
# m条2维数据
x = np.random.randn(m)
y = np.random.randn(m)
data = np.stack([x, y], axis=1) # m, 2
# print(data.shape)
else:
if os.path.basename(path)[-3:] == 'csv':
df = pd.read_csv(path)
data = df.loc[:, df.columns!= 'label']
return np.array(data)
def pca(data, k=99999):
# data: m, n,m条n维数据
mean = np.mean(data, axis=0) # n,
# 去中心化
meadnRemoved = data - mean # m, n
# rowvar = 0, 除的是m-1
# rowvar = 1, 除的是m
cov = np.cov(meadnRemoved, rowvar=0) # n, n
# j个特征值
# n, j j个n维特征向量构成的矩阵
eigVals, eigVecs = np.linalg.eig(cov)# 分解计算协方差矩阵的(特征值 特征向量)
eigValsArgsort = np.argsort(eigVals,)#默认是从小到大
eigValsArgsort = eigValsArgsort[:(-k+1):-1]#倒叙取,取最大的k个
decEigVecs = eigVecs[:, eigValsArgsort] # n, k
decData = np.dot(meadnRemoved, decEigVecs) # m, n n, k --> m, k
dataReverse = np.dot(decData, decEigVecs.T) # m, k k, n -->m, n
meanReverse = np.mean(dataReverse, axis=0)
dataReverse = dataReverse + meanReverse # 通过降维后的数据与变换矩阵还原原数据
eigValsSort = np.sort(eigVals)[::-1] # 所有特征值从大到小排列
eigVals_rotio = eigValsSort / np.sum(eigVals) * 100 # 每个特征值占所有特征值和的比例
# 前i个特征值的和占所有特征值和的比例
eigVals_sum_rotio = np.array([np.sum(eigValsSort[:i]) / np.sum(eigVals) * 100 for i in range(len(eigValsSort))])
return decData, dataReverse, eigVals_rotio, eigVals_sum_rotio
if __name__ == '__main__':
data = load_data(m=1000) # m, 2
decData, dataReverse, ratio, sum_ratio = pca(data, k=1)
# 可视化
fig = plt.figure(figsize=(20,10))
ax1 = fig.add_subplot(131)
ax1.scatter(data[:,0],data[:,1],marker='^',s=90) # 原数据
ax1.scatter(decData[:,0],np.zeros(len(decData)),c='black',) # 降维后的图
ax1.scatter(dataReverse[:,0],dataReverse[:,1],marker='^',s=50,c='red') # 还原的数据
plt.legend(['row data','decomposed data','reversed data'])
ax2 = fig.add_subplot(132)
ax2.plot(np.arange(1, len(ratio) + 1),ratio, marker='^')
plt.xticks(np.arange(1, len(ratio) + 1))
plt.legend(['eigvals ratio'])
ax3 = fig.add_subplot(133)
ax3.plot(np.arange(1, len(sum_ratio) + 1), sum_ratio, marker='^')
plt.xticks(np.arange(1, len(sum_ratio) + 1))
plt.legend(['frst i eigvals sum ratio'])
plt.show()
手写数据集
数据集概述
数据集包括三个csv文件。
sample_submission.csv是提交到kaggle的csv文件格式。train.csv是数据的训练集,包含了784个特征和1个标签列。共42000组数据。test.csv为测试集,包含了784个特征,该数据集没有标签这一列,共28000组数据。
步骤
1. 大致确定主成分的个数的范围。
load_data函数和pca函数不变,把主函数改为以下代码。
if __name__ == '__main__':
path = r'digit-recognizer\train.csv'
data = load_data(path=path) # m, n
decData, dataReverse, ratio, sum_rotio = pca(data,)
fig = plt.figure(figsize=(10,5))
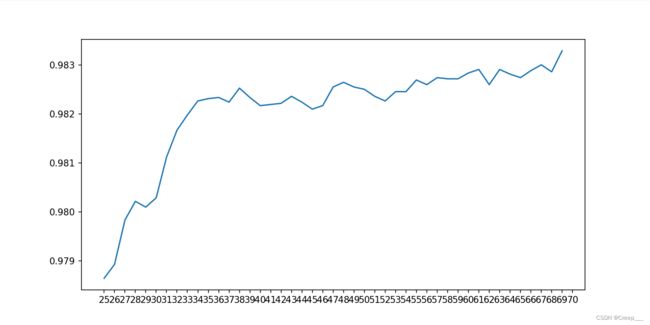
plt.plot(np.arange(1, len(sum_rotio)+1),sum_rotio, )
plt.xticks(np.arange(0, 800, 50))
plt.show()
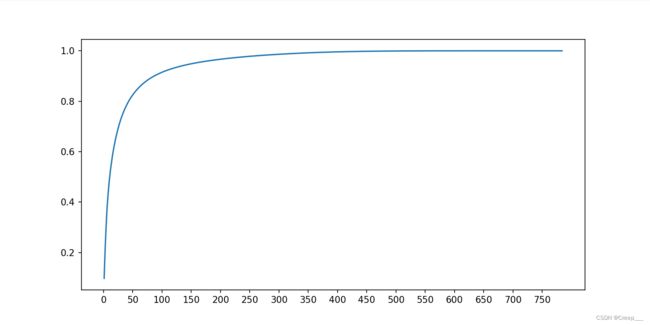
可以看到大概100个时已经达到90%以上了。

2. 进一步确定主成分的个数
从上面分析可以得知主成分在1-100之间,为了进一步确定主成分的个数,取不同的k值使用SVM模型来计算模型的精确度,根据折线图确定。
ps: SVM训练起来真的很慢!可以尝试更换别的算法。
if __name__ == '__main__':
path = r'digit-recognizer\train.csv'
data, label = load_data(path=path) # m, n
n_components = range(1, 101, 10)
scores = []
for i in tqdm(n_components):
decData, dataReverse, ratio, sum_rotio = pca(data, k=i)
clf = SVC(C=200, kernel='rbf')
clf.fit(decData, label)
print("done!")
# X_new = PCA(n_components=i).fit_transform(X)
scores.append(cross_val_score(clf, decData, label, cv=5).mean())
fig = plt.figure(figsize=(10, 5))
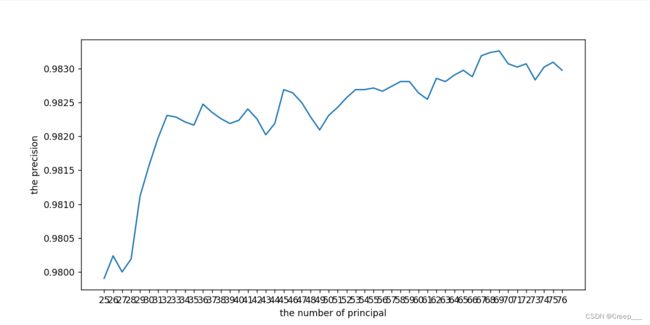
plt.plot(n_components, scores)
plt.xticks(range(0, 101, 10))
plt.show()
结果如图所示。可见大概主成分个数在(25, 78之间精度就达到饱和值了。
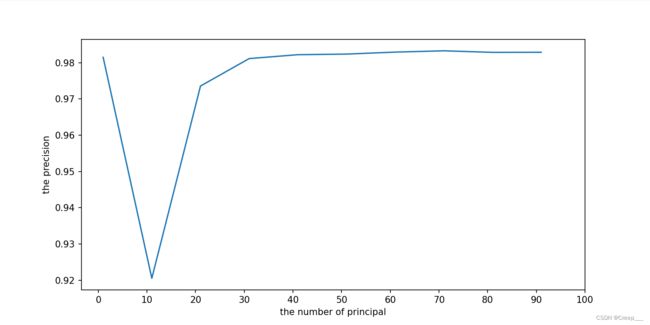
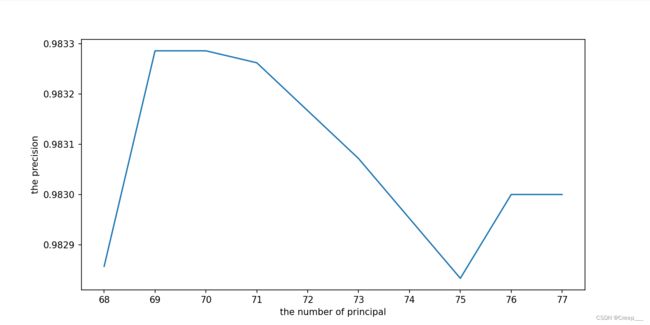
再不断缩小范围。我第一次只设置到了(25, 70,发现最后70的时候还是上涨趋势的,因此又跑了一边(68,78)
if __name__ == '__main__':
path = r'digit-recognizer\train.csv'
data, label = load_data(path=path) # m, n
n_components = range(25, 78)
scores = []
for i in tqdm(n_components):
decData, dataReverse, ratio, sum_rotio = pca(data, k=i)
clf = SVC(C=200, kernel='rbf')
clf.fit(decData, label)
print("done!")
# X_new = PCA(n_components=i).fit_transform(X)
scores.append(cross_val_score(clf, decData, label, cv=5).mean())
fig = plt.figure(figsize=(10, 5))
plt.plot(n_components, scores)
plt.xticks(range(25, 78))
plt.show()
if __name__ == '__main__':
path = r'digit-recognizer\train.csv'
data, label = load_data(path=path) # m, n
decData, dataReverse, ratio, sum_rotio = pca(data, k=70)
knn = KNeighborsClassifier()
score = cross_val_score(knn, decData, label, cv=5).mean()
print(score) # 0.9712380952380952
精度能达到97.12%。
sklearn库实现的PCA
调用sklearn库和自己实现的PCA计算出的结果进行对比,发现几乎是一样的。
path = r'digit-recognizer\train.csv'
data, label = load_data(path=path) # m, n
n_components = range(25, 77, )
scores = []
for i in tqdm(n_components):
pca_instance = PCA(n_components=i)
decData = pca_instance.fit_transform(data)
ratio = pca_instance.explained_variance_ratio_
sum_rotio = np.cumsum(ratio)
clf = SVC(C=200, kernel='rbf')
clf.fit(decData, label)
print("done!")
# X_new = PCA(n_components=i).fit_transform(X)
scores.append(cross_val_score(clf, decData, label, cv=5).mean())
fig = plt.figure(figsize=(10, 5))
plt.plot(n_components, scores)
plt.xticks(range(25, 77,))
plt.show()