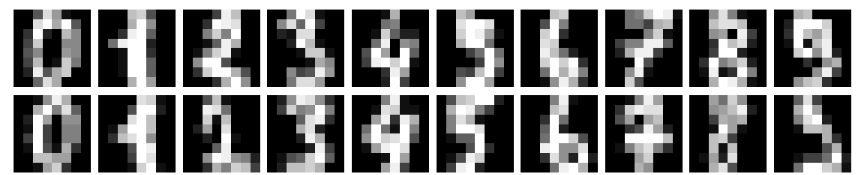3.5 特征提取和降维

特征提取用于提升模型的表示能力
数据降维主要是在不减少模型准确率的情况下减少数据的特征数量

1.主成分分析（PCA）

在多元统计分析中，主成分分析是一种分析、简化数据及、提取主要成分的技术。在实际问题中，特征之间可能存在一定的相关性，在这种情况下就存在重叠的信息，主成分分析可以通过少数的特征来保留原始数据及中的大部分分析，从而减少数据维度。较大的特征值保留数据较为主要的信息，保留的每个主成分是将所有原始数据特征进行线性组合，PCA在保留原始数据主要信息的情况下减少数据的维度。
但是主成分分析效果主要依赖于给定的数据集，数据的准确性对分析结果影响很大。

在大多数实际问题中，训练实例并不是在所有维度上均匀分布的。许多特征几乎是不变的，而其他特征则高度相关（正如前面针对MNIST所讨论的）。因此，所有训练实例都位于（或接近）高维空间的一个低维子空间中。这听起来很抽象，让我们看一个例子。在图中，您可以看到一个由圆表示的三维数据集。

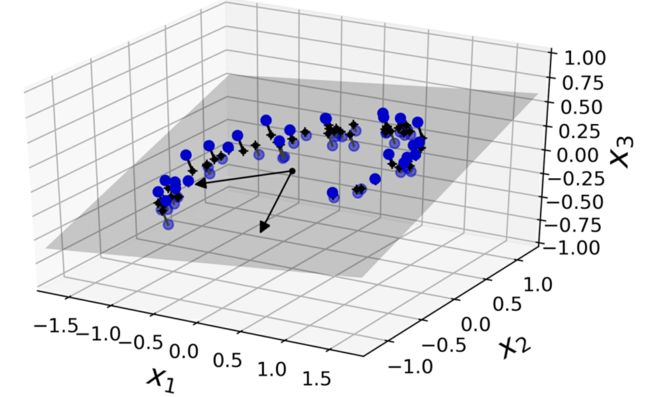
请注意，所有训练实例都靠近一个平面：这是高维（3D）空间的低维（2D）子空间。如果我们将每个训练实例垂直投影到这个子空间上（用连接实例到平面的短线表示），我们得到新的二维数据集，如图8-3所示。我们刚刚将数据集的维数从三维降到了二维，注意轴对应于新的特征z和z（平面上投影的坐标）。

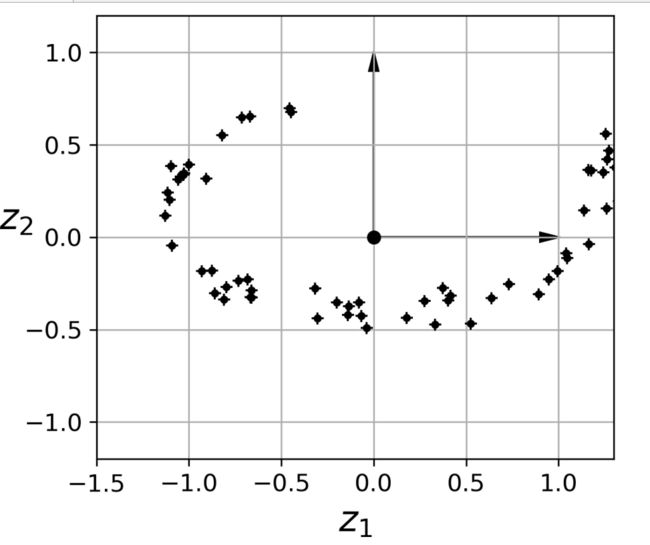
在将训练集投影到低维超平面之前，需要先选择正确的超平面。例如，一个简单的二维数据集如图所示，以及三个不同的轴（即一维超平面）。右侧是数据集投影到每个轴上的结果。如您所见，实线上的投影保留了最大方差，而虚线上的投影保留了非常小的方差，而投影到虚线上则保留了中间的方差。

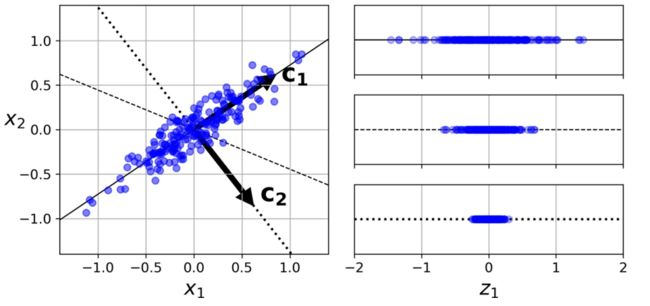
选择保留最大方差的轴似乎是合理的，因为它很可能比其他投影丢失更少的信息。另一种证明这种选择的方法是，正是轴使原始数据集与其投影到该轴上的投影之间的均方距离最小化。这是PCA背后相当简单的想法。主成分主成分分析（PCA）确定了训练集中方差最大的轴。在上图中，它是实线。它还会找到与第一个轴正交的第二个轴，该轴占剩余方差的最大值。在这个2D示例中没有选择：它是虚线。如果它是一个高维数据集，PCA还会找到一个与前两个轴正交的第三个轴，以及第四个、第五个轴，以此类推，其数量与数据集中的维度数相等。
对于每个主成分，PCA会找到一个指向PC方向的零中心单位向量。由于两个相反的单位向量位于同一个轴上，PCA返回的单位向量的方向是不稳定的：如果您稍微扰动训练集并再次运行PCA，单位向量可以指向与原始向量相反的方向。然而，它们通常仍然位于同一轴线上。在某些情况下，一对单位向量甚至可以旋转或交换（如果沿这两个轴的方差接近），但它们定义的平面通常保持不变。

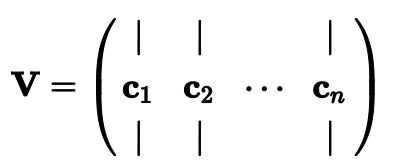
那么如何找到训练集的主要成分呢？有一种称为奇异值分解（SVD）的标准矩阵分解技术，可以将训练集矩阵X分解为三个矩阵的矩阵乘法，其中V包含定义我们要寻找的所有主成分的单位向量，如等式1所示。

一旦确定了所有的主成分，就可以通过将数据集投影到由第一个主成分定义的超平面上，将数据集的维数降到d维。选择此超平面可确保投影将尽可能多地保留方差。例如，在图1中，三维数据集被投影到由前两个主要组件定义的二维平面上，保留了数据集很大一部分的方差。因此，二维投影看起来非常像原始的三维数据集。为了将训练集投影到超平面上并获得维数为d的简化数据集X，计算训练集矩阵X与矩阵W的矩阵相乘，矩阵W定义为包含V的前d列的矩阵，如等式2所示。

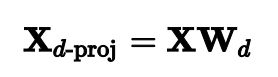
scikitlearn的PCA类使用SVD分解来实现PCA，就像我们在本章前面所做的那样。以下代码应用PCA将数据集的维数降低到两个维度：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy as sp
## 图像在jupyter notebook中显示
%matplotlib inline
## 显示的图片格式（mac中的高清格式），还可以设置为"bmp"等格式

## 主成分分析 PCA
from sklearn.decomposition import PCA
import scipy.io as sio   ## 用来读取mat文件
## ARface数据集，100类，每类26个样本，每个图像32*32
face = sio.loadmat("D:\Desktop\python在机器学习中的应用\AR_face_100classes_26points_per_person_32_32_2600points.mat")
face = face["A"] / 255.0
face.shape

结果显示数据集有2600个人脸，每个图像的特征维度为1024维，对每张图像进行中心化处理（用像素值减去图像均值）

## 人脸数据中心化处理
face = face - face.mean(axis=0)
## PCA降维
## 查看其中的样本
size = 32
plt.figure(figsize=(10,4))
for ii in np.arange(10):
    plt.subplot(2,5,ii+1)
    image = face[:,ii*26].reshape((size,size),order="F") # 'C'（按行排序）和'F'（按列排列）,取了10张图片
    vmax = max(image.max(), -image.min())
    plt.imshow(image,cmap=plt.cm.gray,interpolation='nearest',
                   vmin=-vmax, vmax=vmax)
    plt.axis("off")
plt.subplots_adjust(wspace = 0.1,hspace=0.1)    
plt.show()

*imshow(X, cmap=None, norm=None, aspect=None, interpolation=None, alpha=None, vmin=None, vmax=None, origin=None, extent=None, , filternorm=True, filterrad=4.0, resample=None, url=None, data=None)
用法详细说明
interpolation所使用的插值方法： ‘none’, ‘antialiased’, ‘nearest’, ‘bilinear’, ‘bicubic’, ‘spline16’, ‘spline36’, ‘hanning’, ‘hamming’, ‘hermite’, ‘kaiser’, ‘quadric’, ‘catrom’, ‘gaussian’, ‘bessel’, ‘mitchell’, ‘sinc’, ‘lanczos’.
“无”、“抗锯齿”、“最近点”、“双线性”、“双三次”、“样条16”、“样条36”、“汉宁”、“哈明”、“赫米特”、“凯撒”、“二次曲面”、“卡特罗姆”、“高斯”、“贝塞尔”、“米切尔”、“辛克”、“兰佐斯”。
如果图像上采样超过三倍（即显示像素的数量至少是数据数组大小的三倍），则使用’nearest’插值。

subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=None, hspace=None)
调整子图布局参数。
wspacefloat
填充宽度，作为平均轴宽度的一部分。

hspacefloat
填充高度，作为平均轴高度的一部分。

## 使用pca找到人脸数据中的特征脸数据
pca = PCA(n_components=100,svd_solver = "randomized")
face_pca = pca.fit_transform(face)
face_pca.shape

如果将svd_solver超参数设置为“randomized”，Scikit Learn将使用一种称为随机化PCA的随机算法，该算法可以快速找到第一个主成分的近似值。

np.sum(pca.explained_variance_ratio_)

100张特征人脸数据解释方差（当有多个变量,分析单个变量与总方差的方差比为变量的解释方差）达到97%，保留了数据中大部分信息

plt.figure(figsize=(10,4))
for ii in np.arange(10):
    plt.subplot(2,5,ii+1)
    image = face_pca[:,ii].reshape((size,size),order="F")
    vmax = max(image.max(), -image.min())
    plt.imshow(image,cmap=plt.cm.gray,interpolation='nearest',
                   vmin=-vmax, vmax=vmax)
    plt.axis("off")
plt.subplots_adjust(wspace = 0.1,hspace=0.1)      
plt.show()

前10个用主成分表示的特征脸，大部分数据是戴眼镜的，说明原始数据中含有大量戴眼镜的

2.核成分分析（KPCA）

核技巧，一种将实例隐式映射到一个非常高维空间（称为特征空间）的数学技术，支持向量机实现非线性分类和回归。高维特征空间中的线性决策边界对应于原始空间中的复杂非线性决策边界。结果表明，同样的技巧也可以应用到PCA中，使得对复杂的非线性投影进行降维成为可能。这称为内核PCA（KPCA）。下面的代码使用scikitlearn的KernelPCA类对RBF内核执行KPCA

## 使用核主成分分析 KPCA找到人脸数据的特征脸
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components=100, kernel="rbf")
face_kpca = kpca.fit_transform(face)
face_kpca.shape

由于kPCA是一种无监督的学习算法，因此没有明显的性能指标来帮助选择最佳的核和超参数值。也就是说，降维通常是监督学习任务（例如分类）的准备步骤，因此可以使用网格搜索来选择导致任务最佳性能的内核和超参数。下面的代码创建了一个两步流水线，首先使用kPCA将维度降为二维，然后应用Logistic回归进行分类。然后使用GridSearchCV为kPCA找到最佳的核和gamma值，以便获得最佳的分类精度：

然后通过best_params_u变量获得最佳内核和超参数：


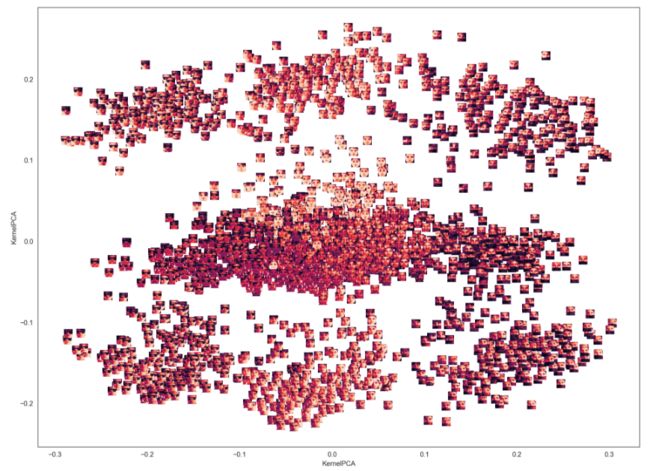
KPCA轮廓更清晰

from matplotlib import offsetbox
plt.figure(figsize=(16,12))
ax = plt.subplot(111)
x = face_kpcaf[:,0]
y = face_kpcaf[:,1]
images = []
for i in range(len(x)):
    x0, y0 = x[i], y[i]
    img = np.reshape(faceT[i,:],(32,32),order = "F")
    image = offsetbox.OffsetImage(img, zoom=0.4)
    ab = offsetbox.AnnotationBbox(image, (x0, y0), xycoords='data', frameon=False)
    images.append(ax.add_artist(ab))
ax.update_datalim(np.column_stack([x, y]))
ax.autoscale()
plt.xlabel("KernelPCA1")
plt.ylabel("KernelPCA2")
plt.show()

两个方向都是分了三个层次，戴围巾、干净的人脸图像、戴墨镜

3.Isomap （流形学习的一种）

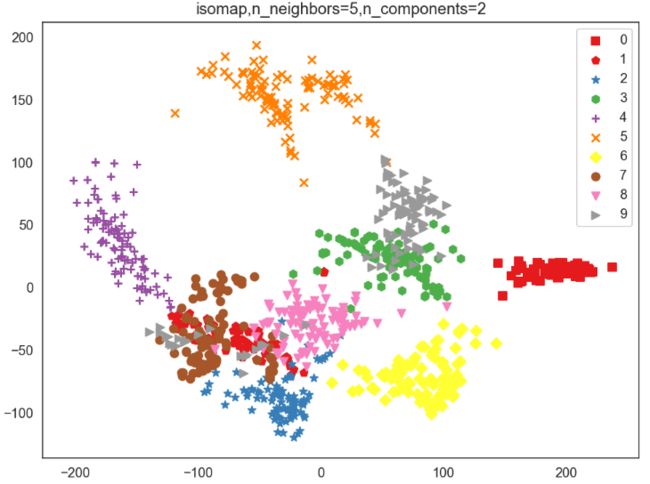
Isomap 流形学习是借鉴拓扑流形概念的一种降维方法，学习通过近邻的距离来计算高维空间种样本点的距离，所以紧邻个数对流形降维得到的结果影响很大
近邻下的降维结果

## Isomap将手写字体数据降维分析
from sklearn.manifold import Isomap
from sklearn.datasets import load_digits
## 10类数据，使用500个样本，图像大小8*8
X,Y = load_digits(return_X_y=True)
X = X[0:1000,:]
Y = Y[0:1000]
X.shape

## 查看其中的数据
size = 8
plt.figure(figsize=(10,2))
for ii in np.arange(20):
    plt.subplot(2,10,ii+1)
    image = X[ii,:].reshape((size,size))
    vmax = max(image.max(), -image.min())
    plt.imshow(image,cmap=plt.cm.gray)
    plt.axis("off")
plt.subplots_adjust(wspace = 0.1,hspace=0.1)    
plt.show()

isomap = Isomap(n_neighbors=5,n_components=2)
im_iso = isomap.fit_transform(X)
shape = ["s","p","*","h","+","x","D","o","v",">"]
plt.figure(figsize=(8,6))
for ii in range(len(np.unique(Y))):
    scatter = im_iso[Y==ii,:]
    plt.scatter(scatter[:,0],scatter[:,1],color=plt.cm.Set1(ii / 10.),marker = shape[ii],label = str(ii))
    plt.legend()
    plt.title("isomap,n_neighbors=5,n_components=2") 
    plt.legend()   
plt.show()

近邻数量不能太多，越多越密集，不能很好区分数据