01等概率发生器、随机函数、对数器
1.数据结构
数据结构:是由连续结构、跳转结构或者连续加跳转(可能有多个叉)结构组成
数据结构是很多算法得以进行的载体
数组:便于寻址不便于删增数据(需要不断移动数据,如果不动可能就不是连续结构)
链表(跳转结构):便于增删数据,通过改指针(改节点)走向就可以删加数据,不便于寻址
2.前缀数组
假设有一个数组arr,用户总是频繁的查询arr中某一段的累加和
你如何组织数据,能让这种查询变得便利和快捷?
**方法一建表:**数组 [3,4,2,1,6,7,8] 适合非常频繁的拿数据,因为方法二还需要做一次减法操作
方法二前缀和方法
数组 [3,2,-1,6,7,2,-2]
定义一个help数组 [3,5,4,10,17,19,17] H[i]表示arr从0到i的累加结果 3~7的累加和=H[7] - H[2]
如果前一个下标为0直接拿后一个下标的H[i],如果不等于0等于H[R] - H[L-1]
public static class RangeSum2 {
private int[] preSum;
public RangeSum2(int[] array) {
int N = array.length;
preSum = new int[N];
preSum[0] = array[0];
for (int i = 1; i < N; i++) {
preSum[i] = preSum[i - 1] + array[i];
}
}
public int rangeSum(int L, int R) {
return L == 0 ? preSum[R] : preSum[R] - preSum[L - 1];
}
}
3.随机函数
1.Math.random() ->生成double类型 ->范围[0,1)
Math.random() ->生成double类型 ->范围[0,1) ;修改Math.random() < a,测试多次发现,生成的数是等概率生成的,接近a,这和数学中不一样。
public class Code02_RandToRand {
public static void main(String[] args) {
System.out.println("测试开始");
int testTimes = 10000000;
int count = 0;
for (int i = 0;i<testTimes;i++){
if (Math.random() <0.7){
count ++;
}
}
System.out.println((double)count / (double) testTimes);
}
}
2.将[0,1)变为[0,8)
将[0,1)变为[0,8) 只需要将Math.random() * 8,那么随机生成数出现百分制50的概率就应该是Math.random()*8 <4
//[0,1) -> [0,8)
System.out.println("测试开始");
int testTimes = 10000000;
int count = 0;
for (int i = 0;i<testTimes;i++){
if (Math.random()*8 <4){
count ++;
}
}
System.out.println((double)count / (double) testTimes);
//通过实际数来验证是否为百分制50
System.out.println((double)4 / (double) 8);
3.**[0,K) -> [0,8]**左右均闭合
**[0,K) -> [0,8]**左右均闭合
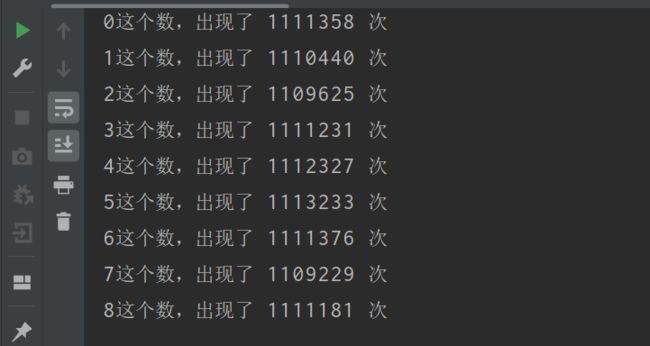
只需要将K赋值为9,验证等概率
int K = 9;
int testTimes = 10000000;
// [0,K) -> [0,8]
int[] counts = new int[9];
for (int i = 0; i < testTimes; i++) {
int answer = (int) (Math.random() * K);
counts[answer]++;
}
for (int i = 0;i<K;i++){
//这里第一个i是对应的整形数,第二个对应的是数组索引
System.out.println(i + "这个数,出现了 " + counts[i] + " 次");
}
每个数出现的次数差不多等概率
4.把得到[0,x)范围上的数的概率从x调整成x^2
如果利用Math.random()函数,
把得到[0,x)范围上的数的概率从x调整成x^2
int testTimes = 10000000;
count = 0;
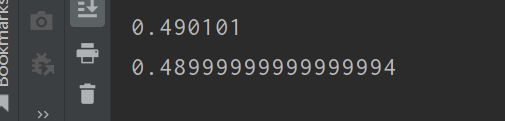
double x = 0.7;
for (int i = 0; i < testTimes; i++) {
if (xToxPower2() < x) {
count++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println(Math.pow(x, 2));
//返回[0,1)的一个小数
//任意的x,x属于[0,1),[0,x)范围上的数出现概率由原来的x调整成x的平方
public static double xToxPower2() {
//如果要生成x^2,就需要用到max函数,因为两次生成随机数是独立的,概率都是x,所以当二者同时发生时,就会有两个max,所以就是x^2,这样也可以保证
//生成的随机数在范围内,因为如果有其中一个不满足就会导致超出范围
return Math.max(Math.random(), Math.random());
//如果是三次方,那就是在二次方的基础上再乘一个max
//return Math.max(Math.random(), Math.max(Math.random(),Math.random()));
}
5.Math.min()
如果使用的是Math.min()
应该是两次都取到1-x的平方,然后1减去就得到最小时的随机函数概率取值1-(1-x)^2
public static void main(String[] args) {
int testTimes = 10000000;
count = 0;
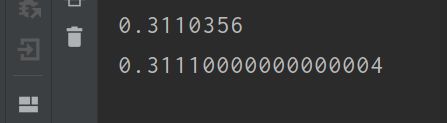
double x = 0.17;
for (int i = 0; i < testTimes; i++) {
if (xToxPower3() < x) {
count++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println((double) 1 - Math.pow((double) 1 - x,2));
public static double xToxPower3() {
return Math.min(Math.random(),Math.random());
}
}
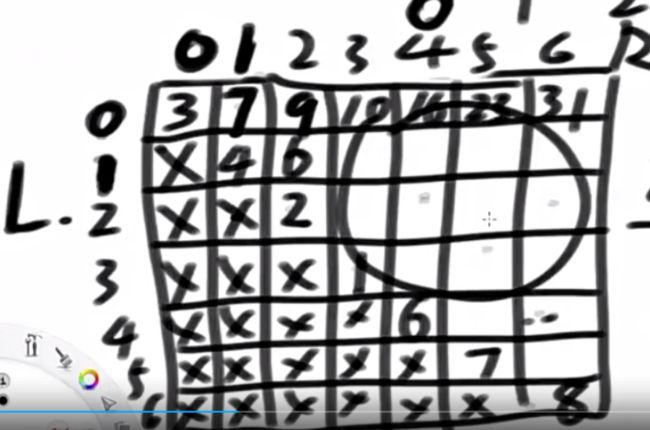
6.将[1,5)随机转换为0、1等概率
public static void main(String[] args) {
int testTimes = 10000000;
count = 0;
for (int i = 0;i <testTimes;i++){
if (f2()==0){
count++;
}
}
System.out.println((double) count / (double) testTimes);
}
public static int f1() {
return (int) (Math.random() * 5 + 1);
}
//随机体制,只能用f1,等概率返回0和1;
public static int f2() {
int ans = 0;
//当f1()为3时就重复执行f1(),当f1()为1、2时为0,当f1()为4、5时为1
do {
ans = f1();
}
while (ans == 3);
return ans < 3 ? 0 : 1;
}
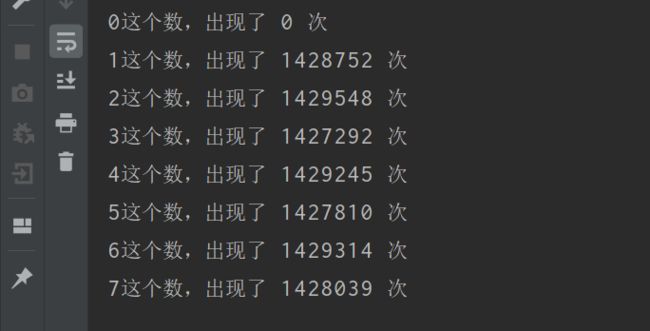
7.得到000~111 做到等概率0~7等概率返回一个
public static void main(String[] args) {
int testTimes = 10000000;
int[] count1 = new int[8];
for (int i = 0; i < testTimes; i++) {
int num = f3();
count1[num]++;
}
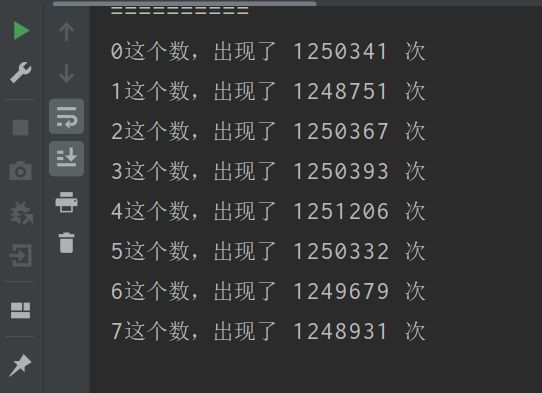
for (int i =0;i<8;i++){
System.out.println(i + "这个数,出现了 " + count1[i] + " 次");
}
}
public static int f1() {
return (int) (Math.random() * 5 + 1);
}
//随机体制,只能用f1,等概率返回0和1;
public static int f2() {
int ans = 0;
//当f1()为3时就重复执行f1(),当f1()为1、2时为0,当f1()为4、5时为1
do {
ans = f1();
}
while (ans == 3);
return ans < 3 ? 0 : 1;
}
//得到000~111 做到等概率0~7等概率返回一个
public static int f3() {
//优先级自高到低的顺序排列为:++、+、<<、<=、&&所以,优先级高的是++,优先级低的是&&。
return (f2() << 2) + (f2() << 1) + f2();
}
}
8.做到等概率0~6等概率返回一个
public static void main(String[] args) {
int testTimes = 10000000;
int[] count1 = new int[8];
for (int i = 0; i < testTimes; i++) {
int num = f3();
count1[num]++;
}
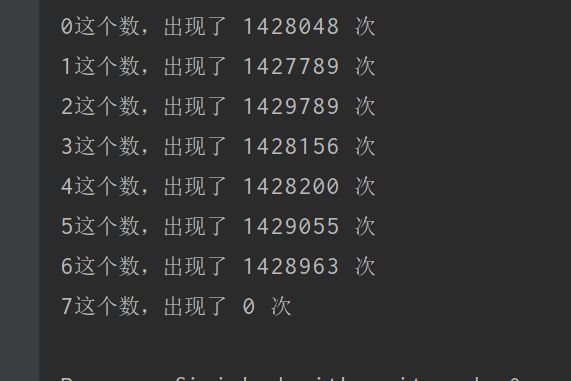
for (int i =0;i<8;i++){
System.out.println(i + "这个数,出现了 " + count1[i] + " 次");
}
}
public static int f1() {
return (int) (Math.random() * 5 + 1);
}
//随机体制,只能用f1,等概率返回0和1;
public static int f2() {
int ans = 0;
//当f1()为3时就重复执行f1(),当f1()为1、2时为0,当f1()为4、5时为1
do {
ans = f1();
}
while (ans == 3);
return ans < 3 ? 0 : 1;
}
//得到000~111 做到等概率0~7等概率返回一个
public static int f3() {
//优先级自高到低的顺序排列为:++、+、<<、<=、&&所以,优先级高的是++,优先级低的是&&。
return (f2() << 2) + (f2() << 1) + f2();
}
// 0 ~ 6等概率返回一个 当f3()为7时就重复执行f3()
public static int f4() {
int ans = 0;
do {
ans = f3();
} while (ans == 7);
return ans;
}
}
9.做到等概率1~7等概率返回一个
public static void main(String[] args) {
int testTimes = 10000000;
int[] count1 = new int[8];
for (int i = 0; i < testTimes; i++) {
int num = g();
count1[num]++;
}
for (int i =0;i<8;i++){
System.out.println(i + "这个数,出现了 " + count1[i] + " 次");
}
}
public static int f1() {
return (int) (Math.random() * 5 + 1);
}
//随机体制,只能用f1,等概率返回0和1;
public static int f2() {
int ans = 0;
do {
ans = f1();
}
while (ans == 3);
return ans < 3 ? 0 : 1;
}
//得到000~111 做到等概率0~7等概率返回一个
public static int f3() {
//优先级自高到低的顺序排列为:++、+、<<、<=、&&所以,优先级高的是++,优先级低的是&&。
return (f2() << 2) + (f2() << 1) + f2();
}
// 0 ~ 6等概率返回一个
public static int f4() {
int ans = 0;
do {
ans = f3();
} while (ans == 7);
return ans;
}
public static int g() {
return f4()+1;
}
}
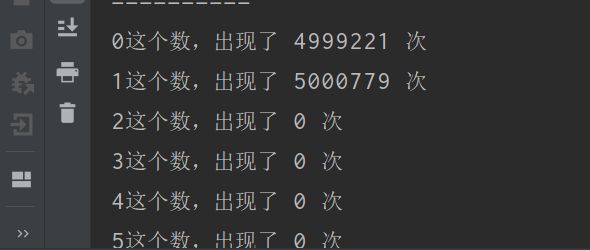
10.非等概率函数变成01等概率发生器
//这里得到0和1不是等概率的只有当p(1-p)时才是等概率的
public static int x(){
return Math.random() < 0.84 ? 0 : 1;
}
//等概率返回0和1
public static int y(){
int ans = 0;
do {
ans = x();
}while (ans == x());//当第二次生成数等于第一次生成数,重做x(),目的在于生成p(1-p)概率事件
// ans = 0 1
// ans = 1 0
return ans;
}
11.选择、冒泡、插入排序的对数器验证
过程
先生成一个随机长度的随机数组—>备份一份数组,作为样本,万一出错有样本可查–>判断第一个数组是否排序成功
为什么要备份?而不是直接相等(=)来备份?
因为如果是直接=来赋值,相当于两个数组都指向同一片内存空间,第一个已经排序好了。这里是按值传递,第一个排序改变,备份的样本不改变,不是引用传递
package class02;
import java.time.OffsetDateTime;
public class Code03_Comp {
public static void selectSort(int[] arr) {
//在进行选择排序之前,先判断边界条件,如果数组为空或者数组长度为2.就不需要我们进行排序
if (arr == null || arr.length < 2) {
return;
}
//其次我们在进行排序时要考虑怎么排序
//先进行0~n-1排序 然后找到一个比0位置小的然后进行交换 然后下次排序0位置就不再进行排序了,从1位置开始,也就是1~n-1 以此类推
//所以我们需要定义一个n也就是数组长度 然后对其进行遍历来找寻需要交换的两个元素
int N = arr.length;
//i为最初的最小元素位置,如果后面有比i位置元素小的元素,将会替换掉i位置所在的最小元素
for (int i = 0; i < N; i++) {
int minValueIndex = i;
for (int j = i + 1; j < N; j++) {
//j为第二个元素的位置,如果它所在位置元素比i位置所在元素小,叫交换二者位置,小于N是因为索引位置不能大于数组的长度
minValueIndex = arr[j] > arr[minValueIndex] ? j : minValueIndex;
}
//最后进行二者的交换
swap(arr, i, minValueIndex);
}
}
//二:交换函数
public static void swap(int[] arr, int i, int j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
//三:打印函数
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
//=====================================================================================================================
//返回一个数组arr,arr长度[0,maxLen-1],arr中的每个值[0,maxValue-1]
public static int[] lenRandomValueRandom(int maxLen, int maxValue) {
int len = (int) (Math.random() * maxLen);
int[] ans = new int[len];
for (int i = 0; i < len; i++) {
ans[i] = (int) (Math.random() * maxValue);
}
return ans;
}
public static int[] copyArray(int[] arr) {
int[] ans = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
ans[i] = arr[i];
}
return ans;
}
public static boolean isSorted(int[] arr) {
if (arr.length < 2) {
return true;
}
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
if (max > arr[i]) {
return false;
}
max = Math.max(max, arr[i]);
}
//如果上面的程序满足。这一条就不再返回,如果上面不满足就同意返回true
return true;
}
public static void main(String[] args) {
int maxLen = 5;
int maxValue = 1000;
int testTime = 100000;
for (int i = 0; i < testTime; i++) {
int[] arr1 = lenRandomValueRandom(maxLen, maxValue);
int[] temp = copyArray(arr1);
selectSort(arr1);
if (!isSorted(arr1)) {
//如果排序出错,isSorted函数就返回false,取反就为true执行if语句
System.out.println(isSorted(arr1));
for(int j = 0;j<temp.length;j++){
System.out.print(temp[j]+" ");
}
System.out.println();
System.out.println("选择排序出错!");
break;
}
}
}
}