论文笔记:You Only Look Once: Unified, Real-Time Object Detection(yolo v1)
一、基本信息
标题:You Only Look Once: Unified, Real-Time Object Detection
时间:2016
引用格式:Redmon, Joseph, et al. “You only look once: Unified, real-time object detection.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
二、研究背景
R-CNN系列都是需要先选取Proposals作为ROI(region of interest),然后输入全连接分类,这种称谓2步骤的网络,事实上不管是最开始的R-CNN,还是Faster R-CNN,bbox的确定都是需要从Proposals的粗略位置进行微调,就是回归预测更精确的位置xy和wh。那么既然都是需要微调,能不能最开始就不用Proposals检测,YOLO就换了一种方式。
而YOLO系列实现的是1步骤网络,核心思想就是省去选取Proposals步骤,而采用网格划分粗略位置,然后使用回归预测进行微调。虽然准确度比不上R-CNN的Proposals + 微调方式,但是速度快了很多。
但是如果能提示速度的情况下也能提高准确度的话,于是就有后面的yolov2 … v3 … v4
R-CNN :输入->选取Proposals(使用SS方法)->卷积->bbox回归
Fast-R-CNN:输入->卷积->选取Proposals(使用SS方法)->bbox回归
Faster-RCNN:输入->卷积->选取Proposals(使用RPN:Anchors组合,进行初次bbox回归)->bbox再次回归
YOLO:输入->卷积->网格(相当于固定位置且粗略的Proposal)->bbox回归
三、创新点
结构
上面就是YOLO使用的网络结构,其基于GoogLeNet,有24个卷积层,2个全连接层。不同的是,YOLO未使用inception
module,而是使用1x1卷积层(此处1x1卷积层的存在是为了跨通道信息整合)+3x3卷积层简单替代。YOLO的最后一层采用线性激活函数,因为需要进行边框回归,其它层都是Leaky ReLU
YOLO更关心的是输出和损失,所以把卷积池化全连接表示成一个单元:
最后用了全连接,所以限制了图片尺寸。
2021年了,这种直觉的做法是卷积直接到7x7。
可以看到YOLO思想非常直白,就是一直卷积池化,直到Feature Map语义够深,Map上一个点接收的视野够广,这时的Map尺寸变得很小(就可以看做是网格,上图就是7 * 7的网格),但是每个点对于输入图片还是对应关系,于是就能通过一Map点预测原图是不是存在物体(前后景区分),以及物体是什么(类别检测),物体的具体位置和大小(bbox回归)。
虽然准确性不及Fast/er-R-CNN,但是速度远超它们,在工业界对于有实时性需求的任务来说非常重要。
输出
用一个Feature Map的点需要预测的东西可多了,上面就说了有:前后景区分、类别检测、 bbox回归
所以一个点的通道数必须非常多,才能对应的起来这么多检测。
下图就是一个Feature Map网格中一个点的表示(可以理解为一个点时30维或者通道数是30):
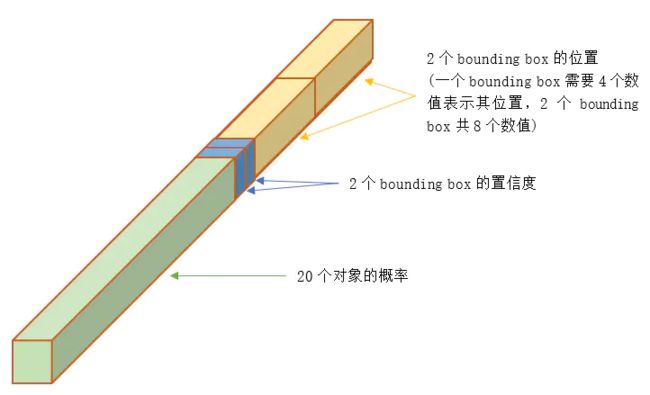
理解上面的30:
30是因为作者论文中任务是预测20个对象。所以每个类别都需要用一个概率输出。
而1个网格实际上是可以代表多个bbox,网格只是说物体的中心在网格对应的这个点上,物体的bbox并没有确定,可以有2个(上面就是2个)、3个、4个…就和Faster R-CNN的RPN中需要用多个Anchor的覆盖更全面的思想一样
但是YOLO的bounding box和Anchor又不太一样:
YOLO并没有预先设置2个bounding box的大小和形状,也没有对每个bounding box分别输出一个对象的预测。它的意思仅仅是对一个对象预测出2个bounding box,选择预测得相对比较准的那个。
作者:X猪
链接:https://www.jianshu.com/p/cad68ca85e27
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。。
同时,一个物体不能有多个bbox,如果选择其中一个作为预测结果,剩下就会被忽略。
一个物体不能有多个gird,即便有时跨越了几个grid,也仅指定其中一个。
所以当多个物体位于同一个gird时,yolo1是处理不了的。
设网格数量为 S*S,每个网格产生B个边框,网络支持识别C个不同的对象。这时,输出的向量长度为:
C + B ∗ ( 4 + 1 ) C+B *(4+1) C+B∗(4+1)
而论文中 C=20 B=2 所以就有上图的长度为30的输出。
整个输出的tensor就是:
S ∗ S ∗ ( C + B ∗ ( 4 + 1 ) ) S * S *(C+B *(4+1)) S∗S∗(C+B∗(4+1))
YOLO选择的参数是 7 * 7网格,2个bounding box,20种对象,因此 输出向量长度 = 20 + 2 * (4+1) = 30。
整个输出的tensor就是 7 * 7 * 30。
损失函数
预测时Confidence是网络预测的, C o n f i d e n c e = P r ( O b j e c t ) ∗ I O U p r e d t r u t h Confidence =Pr(Object)*IOU^{truth}_{pred} Confidence=Pr(Object)∗IOUpredtruth表示的是监督值如何计算。我是这么理解的,Confidence表示的是这个box可信度,预测时当然是输出一个预测值,问题在于训练时的ground truth这么得到的,其实就是当前预测的box框和ground truth框的IoU作为ground truth Confidence。
λ coord ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] + λ coord ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj [ ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] + ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj ( C i − C ^ i ) 2 + λ noobj ∑ i = 0 S 2 ∑ j = 0 B 1 i j noobj ( C i − C ^ i ) 2 + ∑ i = 0 S 2 1 i obj ∑ c ∈ classes ( p i ( c ) − p ^ i ( c ) ) 2 \begin{array}{c} \lambda_{\text {coord }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left[\left(x_{i}-\hat{x}_{i}\right)^{2}+\left(y_{i}-\hat{y}_{i}\right)^{2}\right] \\ +\lambda_{\text {coord }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left[\left(\sqrt{w_{i}}-\sqrt{\hat{w}_{i}}\right)^{2}+\left(\sqrt{h_{i}}-\sqrt{\hat{h}_{i}}\right)^{2}\right] \\ +\sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left(C_{i}-\hat{C}_{i}\right)^{2} \\ +\lambda_{\text {noobj }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {noobj }}\left(C_{i}-\hat{C}_{i}\right)^{2} \\ \quad+\sum_{i=0}^{S^{2}} \mathbb{1}_{i}^{\text {obj }} \sum_{c \in \text { classes }}\left(p_{i}(c)-\hat{p}_{i}(c)\right)^{2} \end{array} λcoord ∑i=0S2∑j=0B1ijobj [(xi−x^i)2+(yi−y^i)2]+λcoord ∑i=0S2∑j=0B1ijobj [(wi−w^i)2+(hi−h^i)2]+∑i=0S2∑j=0B1ijobj (Ci−C^i)2+λnoobj ∑i=0S2∑j=0B1ijnoobj (Ci−C^i)2+∑i=0S21iobj ∑c∈ classes (pi(c)−p^i(c))2
公式中
1 i o b j 1_{i}^{o b j} 1iobj 意思是网格i中存在对象。除了i以外的gird,都不能预测该对象。
1 i j o b j 1_{i j}^{o b j} 1ijobj 意思是网格i的第j个bounding box中存在对象。 除了j以外的bbox,都不能代表该对象。
1 i j n o o b j 1_{i j}^{n o o b j} 1ijnoobj 意思是网格i的第j个bounding box中不存在对象。
言外之意:
1 i j o b j = 1 1_{i j}^{\mathrm{obj}} = 1 1ijobj=1时:
除了i以外的gird,都不能预测该对象。即一个Object只由一个grid来进行预测,不要多个grid都抢着预测同一个Object
除了j以外的bbox,都不能代表该对象。即一个Object只会选择一个具有最大IOU的bbox,此时这个bbox的Confidence = 1,其他bbox的Confidence = 0。
即:
C o n f i d e n c e = P r ( O b j e c t ) ∗ I O U p r e d t r u t h Confidence =Pr(Object)*IOU^{truth}_{pred} Confidence=Pr(Object)∗IOUpredtruth
然后看2个bounding box的IOU,哪个比较大(更接近对象实际的bounding box),就由哪个bounding box来负责预测该对象是否存在,即该bounding box的 P r ( O b j e c t ) = 1 {Pr}(Object)=1 Pr(Object)=1,同时对象真实bounding box的位置也就填入该bounding box。另一个不负责预测的bounding box的 P r ( O b j e c t ) = 0 {Pr}(Object)=0 Pr(Object)=0。
总的来说就是,与对象实际bounding box最接近的那个bounding box,其 C o n f i d e n c e = I O U p r e d t r u t h Confidence =IOU^{truth}_{pred} Confidence=IOUpredtruth,该网格的其它bounding box的 C o n f i d e n c e = 0 Confidence = 0 Confidence=0。
太复了,拆开每项来看:
λ coord ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] \lambda_{\text {coord }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left[\left(x_{i}-\hat{x}_{i}\right)^{2}+\left(y_{i}-\hat{y}_{i}\right)^{2}\right] λcoord i=0∑S2j=0∑B1ijobj [(xi−x^i)2+(yi−y^i)2]
这个就是bbox的中心点误差,只有在 1 i j o b j = 1 1_{i j}^{\mathrm{obj}} = 1 1ijobj=1时,也就是网格i的第j个bounding box中存在对象,网格才计入误差。
λ coord ∑ i = 0 S 2 ∑ j = 0 B 1 i j obj [ ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] \lambda_{\text {coord }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left[\left(\sqrt{w_{i}}-\sqrt{\hat{w}_{i}}\right)^{2}+\left(\sqrt{h_{i}}-\sqrt{\hat{h}_{i}}\right)^{2}\right] λcoord i=0∑S2j=0∑B1ijobj [(wi−w^i)2+(hi−h^i)2]
边框宽度,高度误差,只有在 1 i j o b j = 1 1_{i j}^{\mathrm{obj}} = 1 1ijobj=1时,也就是网格i的第j个bounding box中存在对象,网格才计入误差。
宽度和高度先取了平方根,因为如果直接取差值的话,大的对象对差值的敏感度较低,小的对象对差值的敏感度较高,所以取平方根可以降低这种敏感度的差异,使得较大的对象和较小的对象在尺寸误差上有相似的权重。
∑ i = 0 S 2 ∑ j = 0 B 1 i j obj ( C i − C ^ i ) 2 \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {obj }}\left(C_{i}-\hat{C}_{i}\right)^{2} i=0∑S2j=0∑B1ijobj (Ci−C^i)2
置信度误差,只有在 1 i j o b j = 1 1_{i j}^{\mathrm{obj}} = 1 1ijobj=1时,也就是网格i的第j个bounding box中存在对象,网格才计入误差。
λ noobj ∑ i = 0 S 2 ∑ j = 0 B 1 i j noobj ( C i − C ^ i ) 2 \lambda_{\text {noobj }} \sum_{i=0}^{S^{2}} \sum_{j=0}^{B} \mathbb{1}_{i j}^{\text {noobj }}\left(C_{i}-\hat{C}_{i}\right)^{2} λnoobj i=0∑S2j=0∑B1ijnoobj (Ci−C^i)2
置信度误差,只有在 1 i j o b j = 0 1_{i j}^{\mathrm{obj}} = 0 1ijobj=0时,也就是网格i的第j个bounding box中不存在对象,网格才计入误差。
为不存在对象的bounding box应该老老实实的说"我这里没有对象",也就是输出尽量低的置信度。如果它不恰当的输出较高的置信度,会与真正"负责"该对象预测的那个bounding box产生混淆。其实就像对象分类一样,正确的对象概率最好是1,所有其它对象的概率最好是0。
作者:X猪
链接:https://www.jianshu.com/p/cad68ca85e27
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
∑ i = 0 S 2 1 i obj ∑ c ∈ classes ( p i ( c ) − p ^ i ( c ) ) 2 \sum_{i=0}^{S^{2}} \mathbb{1}_{i}^{\text {obj }} \sum_{c \in \text { classes }}\left(p_{i}(c)-\hat{p}_{i}(c)\right)^{2} i=0∑S21iobj c∈ classes ∑(pi(c)−p^i(c))2
对象分类误差,只有在 1 i j o b j = 1 1_{i j}^{\mathrm{obj}} = 1 1ijobj=1时,也就是网格i的第j个bounding box中存在对象,网格才计入误差。
乘以 λ c o o r d \lambda_{coord} λcoord 调节bounding box位置误差的权重(相对分类误差和置信度误差)。YOLO设置 λ c o o r d = 5 \lambda_{coord} = 5 λcoord=5,即调高位置误差的权
乘以 λ n o o b j \lambda_{noobj} λnoobj 调节不存在对象的bounding box的置信度的权重(相对其它误差)。YOLO设置 λ n o o b j = 0.5 \lambda_{noobj} = 0.5 λnoobj=0.5,即调低不存在对象的bounding box的置信度误差的权重。
其他
NMS
NMS方法并不复杂,其核心思想是:选择得分最高的作为输出,与该输出重叠的去掉,不断重复这一过程直到所有备选处理完。
NMS步骤
YOLO的NMS计算方法如下。
网络输出的7730的张量,在每一个网格中,对象位于第j个bounding box的得分:
S c o r e i j = P ( C i ∣ O b j e c t ) ∗ C o n f i d e n c e j {Score}_{i j}=P\left(C_{i} \mid {Object}\right) * {Confidence}_{j} Scoreij=P(Ci∣Object)∗Confidencej
它代表着某个对象 C i C_i Ci存在于第j个bounding box的可能性。
每个网格有:20个对象的概率*2个bounding box的置信度,共40个得分(候选对象)。49个网格共1960个得分。Andrew Ng建议每种对象分别进行NMS,那么每种对象有 1960/20=98 个得分。
作者:X猪
链接:https://www.jianshu.com/p/cad68ca85e27
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
四、实验结果
五、结论与思考
作者结论
总结
思考
参考
本笔记多个部分摘抄自YOLO v1深入理解,强烈推荐查看,看到过讲解最好的了
yoloV1,看过好多篇,这篇感觉讲的最通俗易懂
YOLO详解




