强化学习实战之Bellman期望方程
MDP:Bellman Expectation Equation
MDP理论介绍
有了之前的理论经验我们现在可以通过一个编程实例来体会Bellman期望方程了。
首先我们导入需要用的包,这里使用了sympy,它的优点是可以用符号来表示公式。
import pandas as pd
import sympy
from sympy import symbols
假设这一样一个场景:小明参加了一场考试,那么就有”及格“和”不及格“两种状态,每种状态下小明都有可能选择”学习“和”玩耍“两个动作,由此可以建立一个MDP模型。我们首先给出环境的动态特性:
# dynamic system: taking exams
dynamic = {
's_': ['fail', 'fail', 'passed', 'passed', 'fail', 'passed'],
'r': [-3, -1, 1, 3, -2, 1],
's': ['fail', 'fail', 'fail', 'passed', 'passed', 'passed'],
'a': ['play', 'learn', 'learn', 'play', 'play', 'learn'],
'P(s_, r|s, a)': ['1', '1-m', 'm', '1-n', 'n', '1'],
}
df = pd.DataFrame(data=dynamic)
# center the text
d = dict(selector="th",
props=[('text-align', 'center')])
df.style.set_properties(**{'width':'10em', 'text-align':'center'}).set_table_styles([d])
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mbQcA0L6-1585808773255)(E:\MARL\notes\images\fail&pass1.png)]
以及相应的策略:
# policy
policy = {
's': ['fail', 'fail', 'passed', 'passed'],
'a': ['play','learn', 'play', 'learn'],
'pi(a|s)': ['1-x', 'x', 'y', '1-y'],
}
df2 = pd.DataFrame(data=policy)
df2.style.set_properties(**{'width':'10em', 'text-align':'center'}).set_table_styles([d])
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-if4Hosqv-1585808773256)(E:\MARL\notes\images\fail&pass2.png)]
回忆一下Bellman期望方程:
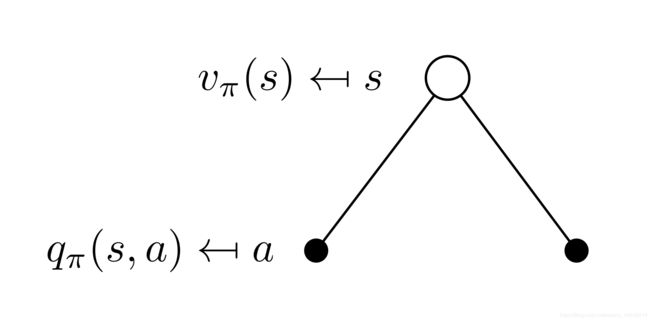

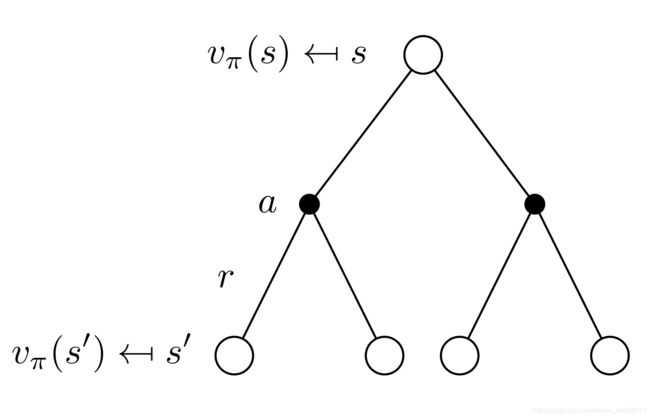
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) ⋅ q π ( s , a ) \begin{aligned}v_{\pi}(s)=\sum_{a \in \mathcal{A}} \pi(a | s) \cdot q_{\pi}(s, a)\\\end{aligned}\\ vπ(s)=a∈A∑π(a∣s)⋅qπ(s,a)
q π ( s , a ) = r ( s , a ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) ⋅ v π ( s ′ ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) ⋅ [ r + γ ⋅ v π ( s ′ ) ] , s ∈ S \begin{aligned}q_{\pi}(s, a)&=r(s,a)+\gamma \sum_{s^{\prime} \in \mathcal{S}} p\left(s^{\prime} | s, a\right)\cdot v_{\pi}\left(s^{\prime}\right)\\&= \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right) \cdot \left[r+\gamma \cdot v_{\pi}(s^{\prime})\right]\quad ,s\in \mathcal{S}\end{aligned} qπ(s,a)=r(s,a)+γs′∈S∑p(s′∣s,a)⋅vπ(s′)=s′,r∑p(s′,r∣s,a)⋅[r+γ⋅vπ(s′)],s∈S
根据这两个公式一共可以列出6个方程
'''
Bellman Equation
v(fail) = pi(play|fail)*q(fail,play) + pi(learn|fail)*q(fail,learn)
= (1-x)*q(fail,play) + x*q(fail,learn)
v(passed) = pi(play|passed)*q(passed,play) + pi(learn|passed)*q(passed,learn)
= y*q(passed,play) + (1-y)*q(passed,learn)
q(fail,play) = P(fail,r|fail,play)[r + gamma*v(fail)] + P(passed,r|fail,play)[r + gamma*v(passed)]
= 1*[-3 + gamma*v(fail)] + 0
= -3 + gamma*v(fail)
q(fail,learn) = P(fail,r|fail,learn)[r + gamma*v(fail)] + P(passed,r|fail,learn)[r + gamma*v(passed)]
= (1-m)*[-1 + gamma*v(fail)] + m*[1 + gamma*v(passed)]
q(passed,play) = P(fail,r|passed,play)[r + gamma*v(fail)] + P(passed,r|passed,play)[r + gamma*v(passed)]
= n*[-2 + gamma*v(fail)] + (1-n)*[3 + gamma*v(passed)]
q(passed,learn) = P(fail,r|passed,learn)[r + gamma*v(fail)] + P(pass,r|passed,learn)[r + gamma*v(passed)]
= (1-m)*0 + m*[1 + gamma*v(pass)]
= m[1 + gamma*v(pass)]
6 virables, 6 equations; m,n,gamma are parameters in (0,1)
'''
# automatically enable the best printer available in your environment.
sympy.init_printing()
# define variables and parameters
v_fail, v_passed = symbols('v_(fail) v_(passed)')
q_fail_play, q_fail_learn ,q_passed_play, q_passed_learn = symbols('q_(fail\,play) q_(fail\,learn) q_(passed\,play) q_(passed\,learn)')
m, n, gamma, x, y = symbols('m n gamma x y')
# define the augmented matrix
system = sympy.Matrix((
(1, 0, x-1, -x, 0, 0, 0),
(0, 1, 0, 0, -y, y-1, 0),
(-gamma, 0, 1, 0, 0, 0, -3),
((m-1)*gamma, -m*gamma, 0, 1, 0, 0, 2*m-1),
(-n*gamma, (n-1)*gamma, 0, 0, 1, 0, 3-5*n),
(0, -m*gamma, 0, 0, 0, 1, m),
))
system
这是一个增广矩阵,解之可得价值函数
[ 1 0 x − 1 − x 0 0 0 0 1 0 0 − y y − 1 0 − γ 0 1 0 0 0 − 3 γ ( m − 1 ) − γ m 0 1 0 0 2 m − 1 − γ n γ ( n − 1 ) 0 0 1 0 3 − 5 n 0 − γ m 0 0 0 1 m ] \displaystyle \left[\begin{matrix}1 & 0 & x - 1 & - x & 0 & 0 & 0\\0 & 1 & 0 & 0 & - y & y - 1 & 0\\- \gamma & 0 & 1 & 0 & 0 & 0 & -3\\\gamma \left(m - 1\right) & - \gamma m & 0 & 1 & 0 & 0 & 2 m - 1\\- \gamma n & \gamma \left(n - 1\right) & 0 & 0 & 1 & 0 & 3 - 5 n\\0 & - \gamma m & 0 & 0 & 0 & 1 & m\end{matrix}\right] ⎣⎢⎢⎢⎢⎢⎢⎡10−γγ(m−1)−γn0010−γmγ(n−1)−γmx−101000−x001000−y00100y−1000100−32m−13−5nm⎦⎥⎥⎥⎥⎥⎥⎤
sympy.solve_linear_system(
system,
v_fail, v_passed,
q_fail_play, q_fail_learn, q_passed_play, q_passed_learn
)
q ( f a i l , l e a r n ) : 3 γ 2 m n y ( x − 1 ) − 3 γ 2 m ( m − 1 ) ( x − 1 ) ( y − 1 ) − 3 γ 2 y ( m − 1 ) ( n − 1 ) ( x − 1 ) − γ m 2 ( y − 1 ) ( γ ( x − 1 ) + 1 ) − γ m y ( 5 n − 3 ) ( γ ( x − 1 ) + 1 ) − 3 γ ( m − 1 ) ( x − 1 ) + ( 2 m − 1 ) ( γ 2 m ( x − 1 ) ( y − 1 ) + γ 2 y ( n − 1 ) ( x − 1 ) + γ m ( y − 1 ) + γ y ( n − 1 ) + γ ( x − 1 ) + 1 ) − γ 2 m n x y + γ 2 m x ( m − 1 ) ( y − 1 ) + γ 2 m ( x − 1 ) ( y − 1 ) + γ 2 x y ( m − 1 ) ( n − 1 ) + γ 2 y ( n − 1 ) ( x − 1 ) + γ m ( y − 1 ) + γ x ( m − 1 ) + γ y ( n − 1 ) + γ ( x − 1 ) + 1 , q ( f a i l , p l a y ) : − 2 γ 2 m 2 x y + 2 γ 2 m 2 x − 3 γ 2 m n x y + 6 γ 2 m x y − 2 γ 2 m x + 2 γ 2 n x y − 2 γ 2 x y − γ m x − 3 γ m y + 3 γ m − 3 γ n y + 2 γ x + 3 γ y − 3 γ 2 m 2 x y − γ 2 m 2 x − γ 2 m x y − γ 2 m y + γ 2 m − γ 2 n y + γ 2 y + γ m x + γ m y − γ m + γ n y − γ y − γ + 1 , q ( p a s s e d , l e a r n ) : m ( − 3 γ 2 m n x y + 2 γ 2 m x y + 2 γ 2 n x y + γ 2 n y − 2 γ 2 y + γ m x − 4 γ n y + 2 γ y − γ + 1 ) γ 2 m 2 x y − γ 2 m 2 x − γ 2 m x y − γ 2 m y + γ 2 m − γ 2 n y + γ 2 y + γ m x + γ m y − γ m + γ n y − γ y − γ + 1 , q ( p a s s e d , p l a y ) : 3 γ 2 m n ( x − 1 ) ( y − 1 ) + γ m ( y − 1 ) ( − γ m n x + γ x ( m − 1 ) ( n − 1 ) + γ ( n − 1 ) ( x − 1 ) + n − 1 ) + γ n x ( 2 m − 1 ) ( γ m ( y − 1 ) + 1 ) + 3 γ n ( x − 1 ) − ( 5 n − 3 ) ( γ 2 m x ( m − 1 ) ( y − 1 ) + γ 2 m ( x − 1 ) ( y − 1 ) + γ m ( y − 1 ) + γ x ( m − 1 ) + γ ( x − 1 ) + 1 ) − γ 2 m n x y + γ 2 m x ( m − 1 ) ( y − 1 ) + γ 2 m ( x − 1 ) ( y − 1 ) + γ 2 x y ( m − 1 ) ( n − 1 ) + γ 2 y ( n − 1 ) ( x − 1 ) + γ m ( y − 1 ) + γ x ( m − 1 ) + γ y ( n − 1 ) + γ ( x − 1 ) + 1 , v ( f a i l ) : − γ m 2 x ( y − 1 ) − γ m x y ( 5 n − 3 ) + 3 γ m ( x − 1 ) ( y − 1 ) + 3 γ y ( n − 1 ) ( x − 1 ) + x ( 2 m − 1 ) ( γ m ( y − 1 ) + γ y ( n − 1 ) + 1 ) + 3 x − 3 − γ 2 m n x y + γ 2 m x ( m − 1 ) ( y − 1 ) + γ 2 m ( x − 1 ) ( y − 1 ) + γ 2 x y ( m − 1 ) ( n − 1 ) + γ 2 y ( n − 1 ) ( x − 1 ) + γ m ( y − 1 ) + γ x ( m − 1 ) + γ y ( n − 1 ) + γ ( x − 1 ) + 1 , v ( p a s s e d ) : γ n x y ( 2 m − 1 ) + 3 γ n y ( x − 1 ) − m ( γ x ( m − 1 ) ( y − 1 ) + γ ( x − 1 ) ( y − 1 ) + y − 1 ) − y ( 5 n − 3 ) ( γ x ( m − 1 ) + γ ( x − 1 ) + 1 ) − γ 2 m n x y + γ 2 m x ( m − 1 ) ( y − 1 ) + γ 2 m ( x − 1 ) ( y − 1 ) + γ 2 x y ( m − 1 ) ( n − 1 ) + γ 2 y ( n − 1 ) ( x − 1 ) + γ m ( y − 1 ) + γ x ( m − 1 ) + γ y ( n − 1 ) + γ ( x − 1 ) + 1 q_{(fail,learn)} : \frac{3 \gamma^{2} m n y \left(x - 1\right) - 3 \gamma^{2} m \left(m - 1\right) \left(x - 1\right) \left(y - 1\right) - 3 \gamma^{2} y \left(m - 1\right) \left(n - 1\right) \left(x - 1\right) - \gamma m^{2} \left(y - 1\right) \left(\gamma \left(x - 1\right) + 1\right) - \gamma m y \left(5 n - 3\right) \left(\gamma \left(x - 1\right) + 1\right) - 3 \gamma \left(m - 1\right) \left(x - 1\right) + \left(2 m - 1\right) \left(\gamma^{2} m \left(x - 1\right) \left(y - 1\right) + \gamma^{2} y \left(n - 1\right) \left(x - 1\right) + \gamma m \left(y - 1\right) + \gamma y \left(n - 1\right) + \gamma \left(x - 1\right) + 1\right)}{- \gamma^{2} m n x y + \gamma^{2} m x \left(m - 1\right) \left(y - 1\right) + \gamma^{2} m \left(x - 1\right) \left(y - 1\right) + \gamma^{2} x y \left(m - 1\right) \left(n - 1\right) + \gamma^{2} y \left(n - 1\right) \left(x - 1\right) + \gamma m \left(y - 1\right) + \gamma x \left(m - 1\right) + \gamma y \left(n - 1\right) + \gamma \left(x - 1\right) + 1}, \\ q_{(fail,play)} : \frac{- 2 \gamma^{2} m^{2} x y + 2 \gamma^{2} m^{2} x - 3 \gamma^{2} m n x y + 6 \gamma^{2} m x y - 2 \gamma^{2} m x + 2 \gamma^{2} n x y - 2 \gamma^{2} x y - \gamma m x - 3 \gamma m y + 3 \gamma m - 3 \gamma n y + 2 \gamma x + 3 \gamma y - 3}{\gamma^{2} m^{2} x y - \gamma^{2} m^{2} x - \gamma^{2} m x y - \gamma^{2} m y + \gamma^{2} m - \gamma^{2} n y + \gamma^{2} y + \gamma m x + \gamma m y - \gamma m + \gamma n y - \gamma y - \gamma + 1}, \\ q_{(passed,learn)} : \frac{m \left(- 3 \gamma^{2} m n x y + 2 \gamma^{2} m x y + 2 \gamma^{2} n x y + \gamma^{2} n y - 2 \gamma^{2} y + \gamma m x - 4 \gamma n y + 2 \gamma y - \gamma + 1\right)}{\gamma^{2} m^{2} x y - \gamma^{2} m^{2} x - \gamma^{2} m x y - \gamma^{2} m y + \gamma^{2} m - \gamma^{2} n y + \gamma^{2} y + \gamma m x + \gamma m y - \gamma m + \gamma n y - \gamma y - \gamma + 1}, \\ q_{(passed,play)} : \frac{3 \gamma^{2} m n \left(x - 1\right) \left(y - 1\right) + \gamma m \left(y - 1\right) \left(- \gamma m n x + \gamma x \left(m - 1\right) \left(n - 1\right) + \gamma \left(n - 1\right) \left(x - 1\right) + n - 1\right) + \gamma n x \left(2 m - 1\right) \left(\gamma m \left(y - 1\right) + 1\right) + 3 \gamma n \left(x - 1\right) - \left(5 n - 3\right) \left(\gamma^{2} m x \left(m - 1\right) \left(y - 1\right) + \gamma^{2} m \left(x - 1\right) \left(y - 1\right) + \gamma m \left(y - 1\right) + \gamma x \left(m - 1\right) + \gamma \left(x - 1\right) + 1\right)}{- \gamma^{2} m n x y + \gamma^{2} m x \left(m - 1\right) \left(y - 1\right) + \gamma^{2} m \left(x - 1\right) \left(y - 1\right) + \gamma^{2} x y \left(m - 1\right) \left(n - 1\right) + \gamma^{2} y \left(n - 1\right) \left(x - 1\right) + \gamma m \left(y - 1\right) + \gamma x \left(m - 1\right) + \gamma y \left(n - 1\right) + \gamma \left(x - 1\right) + 1}, \\ v_{(fail)} : \frac{- \gamma m^{2} x \left(y - 1\right) - \gamma m x y \left(5 n - 3\right) + 3 \gamma m \left(x - 1\right) \left(y - 1\right) + 3 \gamma y \left(n - 1\right) \left(x - 1\right) + x \left(2 m - 1\right) \left(\gamma m \left(y - 1\right) + \gamma y \left(n - 1\right) + 1\right) + 3 x - 3}{- \gamma^{2} m n x y + \gamma^{2} m x \left(m - 1\right) \left(y - 1\right) + \gamma^{2} m \left(x - 1\right) \left(y - 1\right) + \gamma^{2} x y \left(m - 1\right) \left(n - 1\right) + \gamma^{2} y \left(n - 1\right) \left(x - 1\right) + \gamma m \left(y - 1\right) + \gamma x \left(m - 1\right) + \gamma y \left(n - 1\right) + \gamma \left(x - 1\right) + 1}, \\ v_{(passed)} : \frac{\gamma n x y \left(2 m - 1\right) + 3 \gamma n y \left(x - 1\right) - m \left(\gamma x \left(m - 1\right) \left(y - 1\right) + \gamma \left(x - 1\right) \left(y - 1\right) + y - 1\right) - y \left(5 n - 3\right) \left(\gamma x \left(m - 1\right) + \gamma \left(x - 1\right) + 1\right)}{- \gamma^{2} m n x y + \gamma^{2} m x \left(m - 1\right) \left(y - 1\right) + \gamma^{2} m \left(x - 1\right) \left(y - 1\right) + \gamma^{2} x y \left(m - 1\right) \left(n - 1\right) + \gamma^{2} y \left(n - 1\right) \left(x - 1\right) + \gamma m \left(y - 1\right) + \gamma x \left(m - 1\right) + \gamma y \left(n - 1\right) + \gamma \left(x - 1\right) + 1} q(fail,learn):−γ2mnxy+γ2mx(m−1)(y−1)+γ2m(x−1)(y−1)+γ2xy(m−1)(n−1)+γ2y(n−1)(x−1)+γm(y−1)+γx(m−1)+γy(n−1)+γ(x−1)+13γ2mny(x−1)−3γ2m(m−1)(x−1)(y−1)−3γ2y(m−1)(n−1)(x−1)−γm2(y−1)(γ(x−1)+1)−γmy(5n−3)(γ(x−1)+1)−3γ(m−1)(x−1)+(2m−1)(γ2m(x−1)(y−1)+γ2y(n−1)(x−1)+γm(y−1)+γy(n−1)+γ(x−1)+1),q(fail,play):γ2m2xy−γ2m2x−γ2mxy−γ2my+γ2m−γ2ny+γ2y+γmx+γmy−γm+γny−γy−γ+1−2γ2m2xy+2γ2m2x−3γ2mnxy+6γ2mxy−2γ2mx+2γ2nxy−2γ2xy−γmx−3γmy+3γm−3γny+2γx+3γy−3,q(passed,learn):γ2m2xy−γ2m2x−γ2mxy−γ2my+γ2m−γ2ny+γ2y+γmx+γmy−γm+γny−γy−γ+1m(−3γ2mnxy+2γ2mxy+2γ2nxy+γ2ny−2γ2y+γmx−4γny+2γy−γ+1),q(passed,play):−γ2mnxy+γ2mx(m−1)(y−1)+γ2m(x−1)(y−1)+γ2xy(m−1)(n−1)+γ2y(n−1)(x−1)+γm(y−1)+γx(m−1)+γy(n−1)+γ(x−1)+13γ2mn(x−1)(y−1)+γm(y−1)(−γmnx+γx(m−1)(n−1)+γ(n−1)(x−1)+n−1)+γnx(2m−1)(γm(y−1)+1)+3γn(x−1)−(5n−3)(γ2mx(m−1)(y−1)+γ2m(x−1)(y−1)+γm(y−1)+γx(m−1)+γ(x−1)+1),v(fail):−γ2mnxy+γ2mx(m−1)(y−1)+γ2m(x−1)(y−1)+γ2xy(m−1)(n−1)+γ2y(n−1)(x−1)+γm(y−1)+γx(m−1)+γy(n−1)+γ(x−1)+1−γm2x(y−1)−γmxy(5n−3)+3γm(x−1)(y−1)+3γy(n−1)(x−1)+x(2m−1)(γm(y−1)+γy(n−1)+1)+3x−3,v(passed):−γ2mnxy+γ2mx(m−1)(y−1)+γ2m(x−1)(y−1)+γ2xy(m−1)(n−1)+γ2y(n−1)(x−1)+γm(y−1)+γx(m−1)+γy(n−1)+γ(x−1)+1γnxy(2m−1)+3γny(x−1)−m(γx(m−1)(y−1)+γ(x−1)(y−1)+y−1)−y(5n−3)(γx(m−1)+γ(x−1)+1)
总结
这就是一个完整的通过强行求解Bellman期望方程来进行策略评估的过程,可以看到即使是这么小的一个例子也足以体现Bellman方程的难列、难解。用Bellman最优方程求解最优策略时也同样有这个问题,正是这些问题使我们不得不采用其他方法,也就是后面即将出现的DP,MC,TD等等。
参考资料
《强化学习原理与Python实现》肖智清