入门深度学习——基础知识总结（python代码实现）

入门深度学习——基础知识总结（python代码实现）

目前，AI基本上可以说是烂大街了。几乎什么都可以说使用了AI技术，听起来很拉风，很nb的样子。而其中目前最为火热的非深度学习（Deep Learning）莫属。随着，大数据技术完善和计算硬件的更新换代，深度学习技术的效果在大规模数据上已经击败了之前所有的机器学习算法，取得了非凡的性能。
在有关深度学习的热门话题中，有几个被媒体大肆报道的时间，如下表所示：

年份	事件
2012年	在世界性的图像识别大赛ILSVRC中，使用深度学习技术的Supervision方法取得完胜
2012年	利用谷歌公司开发的深度学习技术，人工智能从YouTube的视频中识别出了猫
2014年	苹果公司将Siri语音识别系统变更为使用深度学习技术的实践
2016年	利用谷歌公司开发的深度学习技术，AlphaGo与世界顶级棋手对决，取得了胜利
2016年	奥迪，宝马等公司将深度学习技术应用到汽车的自动驾驶中

深度学习是基于机器学习的神经网络发展起来的，这些我在之前的博客中介绍了他的来龙去脉，不知道的小伙伴可以点这里传送门了解。但遗憾的是，这么邪乎的东西仍然还是一个黑盒子，基本没有可解释性。其优良性能相当大程度上受到程序员调参的影响，这些参数需要人为赋值，很大程度上可以说是“失之毫厘，差之千里”。而参数的取值，来自程序员对问题和网络模型的理解，以及自己调参的经验。因此，对于入门者来说，想要更好的发挥深度学习的威力，精准的调节参数，了解深度学习的数学基础是有必要的。
PS：这里的参数是指超级参数，这种参数，网络模型一般不会优化。

一、 神经网络的基本知识

深度学习是从神经网络的基础上发展而来的。而对于神经网络的基本原理，我在之前的博客中讲的很清楚了因此这里不再赘述，不清除的读者可以点这里传送门了解，这里大致讲了人们从神经元得到启发设计感知机，进一步改进到神经网络。而深度学习的一大特点就是把其中的隐藏层增多了。注意不是一层两层哦，而是二十层，三十层。这样这个网络可以表示的模型更加丰富，简单来说就是有更大的发挥空间，可以拟合更多的数据，进而达到良好的效果。更棒的是，对于一些无法简单采用数学公式表达的问题，采用深度学习技术，只需要提供数据，他就会自己学习出其中的规律。
如下图所示，神经网络是由一个个神经单元连接而成的网络状，分别是输入测，隐藏层（中间层）和输出层组成，可以看到不同的神经单元相互连接，前一层和下一层都用箭头连接，即神经网络是全连接层。
这里简单介绍下不同层的功能：
输入层：读取给予的神经网络的信息。
隐藏层：实际处理信息（特征提取 feature extraction)。
输出层：显示神经网络的计算出的结果。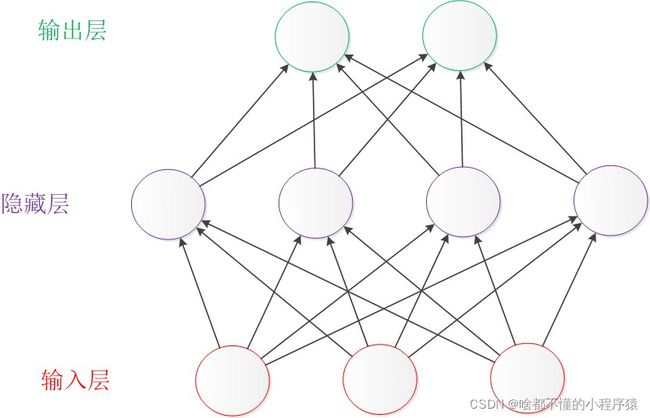

二、神经元——一个简单的开始

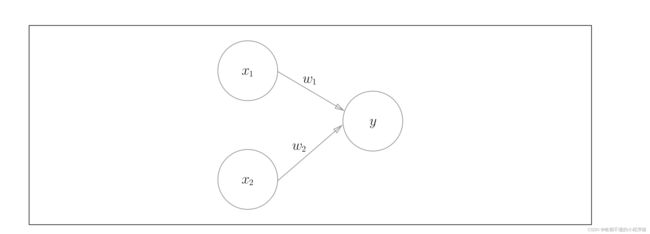
我们先从最简单的感知机开始，如下图所示，图中是一个最为简单的感知机，他有两个输入，一个输出，其中的边表示权值。这个结果就可以表示为$y=x_1{w}_1+x_2{w}_2$,就像一个神经元一样，两个变量x代表输入，一个y代表输出。而对于一个神经元来说，他又一定的阈值。达到这个阈值，他就会刺激下一个神经元，进而传递信息，为了更好的模拟这一效果。我们可以引进一个变量$\mu$,当$y-\mu >0$时代表达到了神经元的阈值，进而产生刺激。传递信息给下一个神经元。反之，小于0那么没有达到阈值，神经元则什么也不做。

三、激活神经元——sigmoid函数

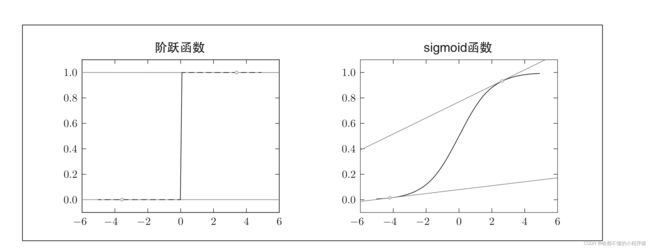
这里为了实现这里效果，我们设计一个函数$f(x)$,当$x>0$时，输出1.当$x<=0$时，输出零。这个函数也叫阶跃函数，如下左图所示：这样固然可以很好的模拟神经元的效果。但是可以看到，这个函数的导数处处为0，在x=0点处导数不存在。这样的函数并不适合计算机运算。此时，你或许会好奇，问什么呢？计算机如何这么刁钻？其实是，当我们在优化参数时，要采用梯度下降算法， 这里就涉及了导数。为了使的函数更加平滑，即处处可导。人们又提出了sigmoid函数，如右图所示。来模拟这个过程，我们使用$\sigma (x)$来表示sigmoid函数，这个函数更加专业的说法叫做激活函数，顾名思义，就是激活神经元，现在也衍生出个更多的激活函数，如relu等。而这个$\mu$叫做偏置，也叫阈值。那么，一个神经元的输出就可以这样表示，$y=\sigma (w_1{x}_1+w_2{x}_2-\mu )$

四、 “异或”问题——给神经网路的一记重击

逻辑数学中，我们会定义“与” “非” “或” “异或"，拿“或”运算来说，其规则是，有1为1，全0为0
，也可以用表格表示,$y=x_1||x_2$：

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	1

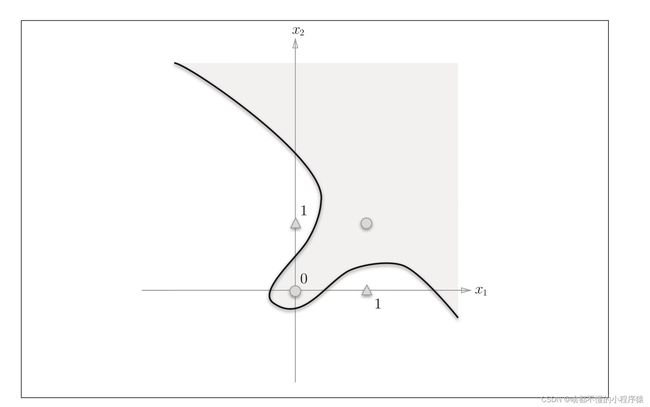
那么这个神经元就可以，通过梯度下降算法(一种优化算法，不清除的读者不必在意)，优化参数$w_1,w_2$，使得y表示为图中一条直线，将其分隔开。进而模拟了与运算。

同样道理，神经元同样可以模拟“非运算”，“与运算”，但对于“异或问题”来说，找不到一个合适的直线解决这个问题。这一记耳光，把神经网络火热的势头彻底扑灭。学者纷纷怀疑神经元的合理性。以至于在那个时代的神经网络论文一概拒收。
诚然这个问题，只能找到一个曲线来解决。但是这个曲面如何表示呢？一个神经元一定时不够的。

五、组合逻辑电路——神经网络的灵感

在组合逻辑电路中，我们是怎么实现一个异或门呢？答案如图所示

它由三个逻辑门电路组合而成，从而实现异或运算。同样道理，我们可不可以把三个神经元也模拟这个过程呢？如下图所示，这是一个两层的神经网络，从第0层到第1层。$s_1,s_2$分别代表前两个逻辑门，第一层到第二层代表第三个逻辑门。这样就理论就可以模拟了异或运算。这样，神经网络有一次展现出强大的实力。

六、层层连接——神经网络诞生

这样我们就回到了开始，这个神经网络，由一个个神经元连接而成的网状结构，被叫做神经网络。进一步来说，我们把中间的层叫做隐藏层，因为我们在使用时，仅仅关注输入数据和我想要的输出数据，中间的层次看不到可以不关心，就像一个黑盒一样。那么这些隐藏层究竟是干肾么的呢？

举一个例子，更好的让大家理解隐藏层，一个直白的说法就是提取特征。我们举一个easyAI的例子说明一下，具体见传送门。我们把深度学习想象成一个水流系统。如图所示，两个入水口，两个输出口。现在我告诉这个网络，输入多少水，需要怎么输出水。他就会自己调节中间流经的水龙头。使得结果符合我的要求。在这种情况下，我会一直告诉网络怎么输出怎么输出。最后，我走了，他就利用这个最终训练好的水龙头流水大小，来对未知的输入水，做出对应的输出。

正如输入一个汉字申的图片，他会把申的结果流出的水最多。从而产生智能。

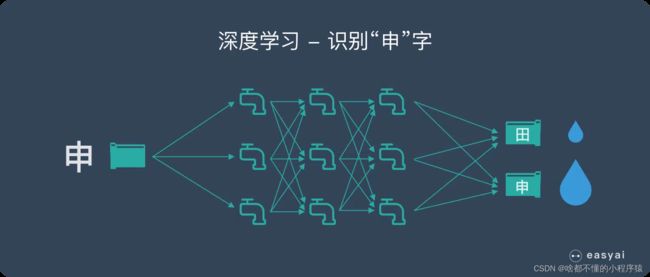
而上述，我根据输入水要求网络输出水的过程叫做正向输入，即从输入层到输出层。

七、反向传播——调节水龙头流水速度

你或许会好奇，怎么产生反向传播呢？即如何调节水龙头流水速度呢？
在刚才的例子中，我们从正向输入水流，网络此时是不可以调节水龙头流速的。此时他会产生一个结果，当然，我要求的一定是其中一个结果。我们会设计一个损失函数，即网络的结果和我们的答案越近，损失值越小，越离谱，损失值越大。得出损失值后，我们会进一步将损失值进一步反向传播通过梯度下降。修正水龙头的流水速度。
这其中的数学推导较为复杂，核心是一层一层递推传播，更新水龙头流水速度。代码实现相当困难，但是，幸运的是目前的深度学习框架，都对其进行的底层实现。我们只需一行代码即可完成。

loss.backward()

其中loss是损失函数。因此，应用网络的程序员完全不用关心其如何传播。这也无关网络性能。因此，不再详细介绍，如果感兴趣的同学，可以自行百度。这里推荐一本数学推导的书<<深度学习的数学>>里面会有详细介绍。

致读者

这样以来，我们才简单的入门了深度学习的数学，第一节比较偏理论。还望大家耐心看完。后面会采用python代码与pytorch深度学习框架来讲解具体的案例，希望大家多多点赞支持。

参考文献

1.《深度学习的数学》杨瑞龙【译】，中国工信出版社，人民邮电出版社
2.《深度学习入门，基于python的理论与实现》陆宇杰【译】，中国工信出版社，人民邮电出版社
3. https://easyai.tech/ai-definition/deep-learning/