吴恩达机器学习课后作业2——逻辑回归（logistic regression）

1. 问题和数据

假设您是一个大学部门的管理员，您想根据申请人在两次考试中的成绩来确定他们的入学机会。您可以使用以前申请人的历史数据作为逻辑回归的训练集。您的任务是构建一个分类模型，根据这两门考试的分数估计申请人被录取的概率。
数据ex2data1.txt内容为一个47行3列(47,3)的数据；其中第一列表示exam1成绩，第二列表示exam2成绩。具体数据如下：

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1

2. 数据导入与初步分析

导入包，numpy和pandas是做运算的库，matplotlib是画图的库。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns  # seaborn与matplotlib在功能上是互补关系
plt.style.use('fivethirtyeight')  # 样式美化
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report  # 这个包是评价报告

导入数据集， 照常，先读取数据观察一下

path = 'ex2data1.txt'
data = pd.read_csv(path, names=['exam1', 'exam2', 'admitted'])
print(data.head())
print(data.describe())

运行输出结果如下：

       exam1      exam2  admitted
0  34.623660  78.024693         0
1  30.286711  43.894998         0
2  35.847409  72.902198         0
3  60.182599  86.308552         1
4  79.032736  75.344376         1

            exam1       exam2    admitted
count  100.000000  100.000000  100.000000
mean    65.644274   66.221998    0.600000
std     19.458222   18.582783    0.492366
min     30.058822   30.603263    0.000000
25%     50.919511   48.179205    0.000000
50%     67.032988   67.682381    1.000000
75%     80.212529   79.360605    1.000000
max     99.827858   98.869436    1.000000

此时由于特征值大小不同需要进行均值归一化。
如果这个房子价格不归一化，它的数量级和你输入值规一化数量级差别太大，几十万的数量级和个位小数做回归，就不能保证收敛了，预测的y和实际上y误差几十万差的太多了。

data2 = (data2 - data2.mean()) / data2.std()  # 这是标准通用的均值归一化公式
print(data2.head())

均值归一化之后数据大小就很均匀，均值归一化结果：

          0         1         2
0  0.130010 -0.223675  0.475747
1 -0.504190 -0.223675 -0.084074
2  0.502476 -0.223675  0.228626
3 -0.735723 -1.537767 -0.867025
4  1.257476  1.090417  1.595389

逻辑回归的本质就是线性回归中嵌套一个sigmoid函数，为了把与预测结果分到（0，1）这个区间
，其中大于0.5的就是A类别，小于0.5的就是B类别。

 

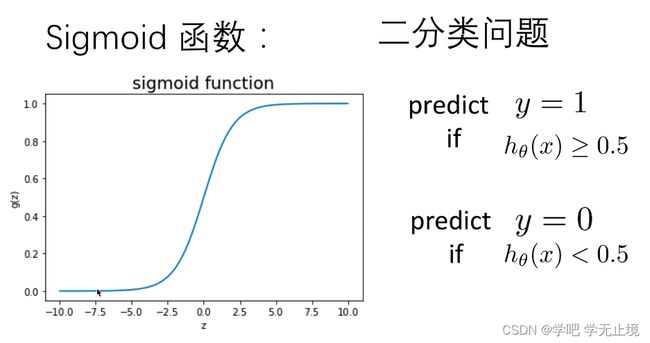
本问题的解决方案其实和线性回归如出一辙，只不过在假设函数这里多了一个sigmoid嵌套函数。

 

     

总结就是：

 

实现sigmoid函数

def sigmoid(z):
    return 1 / (1+np.exp(-z))

实现逻辑回归的代价函数，两个部分，$-y(log(h_{\theta }(x))和-(1-y)log(1-h_{\theta }(x))$

def computeCost(X, y, theta):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T) + 1e-5))  # 结果是个（100，1）矩阵
    second = np.multiply((1-y), np.log(1 - sigmoid(X * theta.T) + 1e-5))  # 结果也是个（100，1）矩阵
    return np.sum(first - second) / (len(X))

现在我们来做一些变量初始化。

data.insert(0, 'ones', 1)# 让我们在训练集中添加一列，以便我们可以使用向量化的解决方案来计算代价和梯度。在训练集的左侧插入一列全为1的列，以便
# 计算即x0=1 loc为O, name为ones,value为1.
# 看下data共有多少列
cols = data.shape[1]  # 表示得到data一共有4列，即cols=4
print("看看有多少列:",  cols)
# pandas中利用.iloc选取数据loc; ','前的部分标明选取的行，','后的部分标明选取的列。
X = data.iloc[:, : cols-1]
y = data.iloc[:, cols-1: cols]
theta = np.full((1, X.shape[1]), 0)    # np.full((行数，列数)， 想要填充的数字)

代价函数是应该是numpy矩阵，所以我们需要转换x和y成矩阵，然后才能使用它们。 我们还需要初始化theta，即把theta所有元素都设置为0。

# pandas读取的数据是DataFrame形式，优势是能对数据进行很多操作,但要想进行矩阵运算，要将DataFrame形式转换为矩阵，例如x=np.matrix(X.values)
# 将X和y转换为矩阵
X = np.matrix(X.values)
y = np.matrix(y.values)

3. 批量梯度下降（Batch gradient decent）

关键点在于theta0和thata1要同时更新，需要用temp进行临时存储。
temp[0, j]这一行是$\theta$的迭代公式，也是梯度下降函数的核心。也就是：

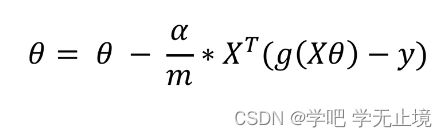
def gradientDescent(X, y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = sigmoid(X @ theta.T) - y  # 计算出每一组数据的误差，每行都是样本的误差

        for j in range(parameters):
            term = np.multiply(error, X[:, j])   # X[ : , j]的意思是X[所有行，第j列]
            temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))   # 前面转不转置和上课学的公式不太一样，这没关系，因为书
            # 上的转置是考虑了求和，我们这里的转置是为了变成可以相乘的方块，至于求和最后用了sum直接求

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

初始化学习速率和迭代次数

alpha = 0.004  # 看up主ladykaka007设置的
iters = 200000  # 看up主ladykaka007设置的; 设置为400000迭代曲线效果就很明显

#调用梯度下降函数，计算迭代后的最优值

g, cost = gradientDescent(X, y, theta, alpha, iters)
# g为迭代完之后的theta;（按return的theta， cost排序）
print("g:", g)

print("cost", cost)

输出最优值g、迭代的各代cost为：

g: [[-23.7738814    0.20685538   0.1999667 ]]
cost [1.9879301  3.38633924 4.52907912 ... 0.25839972 0.24712894 0.25839539]

代入最优值theta，计算最小成本

minCost = computeCost(X, y, g)
print("minCost:", minCost)   # 和up主ladykaka007的结果差不多，她是minCost0.26，我是0.25839

输出最小成本为：

minCost: 0.25839538944259954

预测函数：

def predict(X, theta):
    prob = sigmoid(X @ theta.T)  # 结果prob是一个（100，1）矩阵
    return [1 if x >= 0.5 else 0 for x in prob]  # 遍历prob这个（100，1）矩阵，如果其中数大于0.5，就预测于1，即为通过exam;否则为0，
    # 即未通过exam

y_=np.array(predict(X, g))  # 将最终的g(即最优值theta)代入X*theta.T,让矩阵X与最优的theta挨个乘，得到一个(100, 1)的矩阵
y_pre = y_.reshape(len(y_), 1)  # .reshape(a,b)表示以a行b列的数组形式显示，即将y_表示为(100，1)矩阵形式（虽然本来就长这样,但将它从数组变成了矩阵？）
admi = np.mean(y_pre == y)  # x == y表示两个数组中的值相同时，输出True；否则输出False，其中True=1,False=0;即可得到一个（100，1）的矩阵，
# 其中预测值的y_pre与真实y之间吻合的那行就是1，不吻合的那行就是0。np.mean()为计算矩阵的均值，即为正确率

print("预测正确的概率：", admi)

输出的预测准确率：

预测正确的概率： 0.91

画决策边界：
可以推导出：关于$x_1,x_2$的公式，为一条直线。

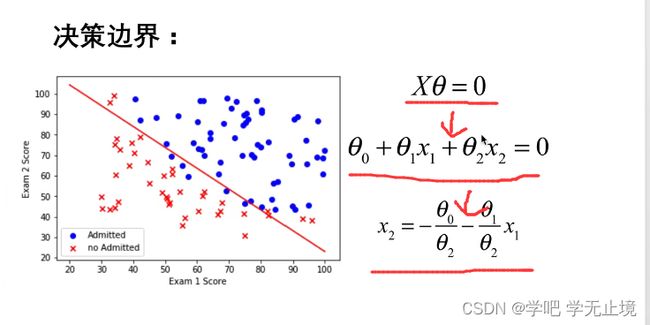
coef1 = -g[0, 0] / g[0, 2]
coef2 = -g[0, 1] / g[0, 2]

x = np.linspace(20, 100, 100) #  # 从最小数据到最大数据（即所有数据）中随机抽100个数据点，用np.linspace可以将这些点用等差数列排列出来，即
# 得到一个个间隔均匀的x点
f = coef1 + coef2 * x
fig, ax = plt.subplots(figsize=(12, 8))  # fig代表绘图窗口(Figure)；ax代表这个绘图窗口上的坐标系(axis)，一般会继续对ax进行操作
ax.scatter(data[data['admitted'] == 0]['exam1'], data[data['admitted'] == 0]['exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['admitted'] == 1]['exam1'], data[data['admitted'] == 1]['exam2'], c='b', marker='o', label='y=1')
ax.legend(loc=1) # 标签位置默认
ax.set(xlabel='exam1',
       ylabel='exam2')
ax.plot(x, f, c='g')
plt.show()  # 数图上分错的点有9个，总共100个点，说明正确率有91%，和弹幕大家一样

输出决策边界图像如下：

画迭代曲线，但是此次的曲线是震荡的，很密集的上下的，所以看起来是一大块红色，但从100000次之后还是开始逐渐收敛的。下图为iters=200000时的迭代曲线，当迭代次数为400000时曲线比较明显。

参考文献：
[1] https://github.com/PlayPurEo/ML-and-DL/blob/master/basic model/2.logistic%20regression/logistic.py
[2] https://www.bilibili.com/video/BV1bt411p74v?p=9&spm_id_from=pageDriver
[3] https://www.bilibili.com/video/BV1Yi4y1P7sJ?spm_id_from=333.999.0.0
[4] hhttps://blog.csdn.net/qq_40918859/article/details/120932686?spm=1001.2101.3001.6650.12&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-12-120932686-blog-88377195.pc_relevant_scanpaymentv1&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-12-120932686-blog-88377195.pc_relevant_scanpaymentv1&utm_relevant_index=16

写在最后： 关于本节的作业二，是一个非线性分类的二元逻辑回归。我一顿操作猛如虎，一看准确率0.5。虽然依然是用的批量梯度下降法，可是不知道问题出在哪，准备先放一放，这些都是比较老的东西，理解原理并会应用就行，不打算死磕，目前时间紧迫，还是准备抓紧时间赶进度。
参考文献 [4] 的文章也是用的批量梯度下降法（但是代码量感觉比我的大了好多），在此先做个标记，以后有空闲了再回来看，顺便试试用正则化的方式求解。