cs231n assignment1 two-layer-net
two-layer-net
首先完成神经网络对scores和损失函数的计算,其中激活函数使用RELU函数,即max(0,x)函数。
neural_net.py的loss()函数
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
h1 = np.maximum(0,X.dot(W1) + b1)
scores = h1.dot(W2) + b2
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# 求指数 (N,C)
exp_scores = np.exp(scores)
# 求和,变为 (N,1)
row_sum = np.sum(exp_scores, axis=1).reshape(N, 1)
norm_scores = exp_scores / row_sum
data_loss = - 1 / N * np.sum(np.log(norm_scores[np.arange(N),y]))
reg_loss = 0.5 * reg * (np.sum(W1 * W1) + np.sum(W2 * W2))
loss = data_loss + reg_loss
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
接下来是反向传播计算梯度,这部分有一定的难度,下面我将我自己的理解记录下来。
整体算法步骤,使用链式求导法则。每一个变量的梯度与该变量的原始大小保持一致。
下面是计算图,从左到右为神经网络正向传递,横线上方为计算得到的值;从右到左为反向传播,横线下方为梯度。

约定,所有的导数均为Loss对该变量的导数,即 d L o s s d 变 量 \frac{d_{Loss}}{d_{变量}} d变量dLoss,因此在程序中 d L o s s d_{Loss} dLoss省略不写,只写出分母。
- 计算 d s c o r e s d_{scores} dscores,即数学表达为 d L o s s d s c o r e s \frac{d_{Loss}}{d_{scores}} dscoresdLoss,因为在data_loss计算过程中将正确分类的得分减去了,故在计算导数过程中需要对正确分类的导数值减一。
- d b 2 d_{b2} db2= d s c o r e s d_{scores} dscores,显然。
- 到了乘法器,可知 d L o s s d h 1 \frac{d_{Loss}}{d_{h_1}} dh1dLoss = d L o s s d s c o r e s d s c o r e s d h 1 \frac{d_{Loss}}{d_{scores}}\frac{d_{scores}}{d_{h_1}} dscoresdLossdh1dscores,本地导数 d s c o r e s d h 1 = W 2 \frac{d_{scores}}{d_{h_1}}=W_2 dh1dscores=W2,故得 d h 1 = W 2 d_{h_1} = W_2 dh1=W2 * d s c o r e s d_{scores} dscores。
- 同理对 d W 2 = h 1 d_{W_2} = h_1 dW2=h1 * d s c o r e s d_{scores} dscores。
- 到了max函数,本地导数结果是:不大于0的导数为0,大于0的导数为本身的值。故 d R e l u = ( h 1 > 0 ) ∗ d h 1 d_{Relu} = (h_1 > 0) * d_{h_1} dRelu=(h1>0)∗dh1
- 然后是 d b 1 d_{b_1} db1同 d R e l u d_{Relu} dRelu。
- 最后是个乘法器,与上面类似。
- 最后对正则化项分别对 W 1 W_1 W1和 W 2 W_2 W2求导,即 d 0.5 ∗ r e g ∗ W 1 ∗ W 1 d W 1 = r e g ∗ W 1 \frac{d_{0.5 *reg * W_1 * W_1}}{d_{W_1}} = reg * W_1 dW1d0.5∗reg∗W1∗W1=reg∗W1 ,同理可以求出 d W 2 {d_{W_2}} dW2 的正则化项。
代码如下:
dscores = norm_scores.copy()
dscores[range(N),y] -= 1
dscores /= N #(N,C)
db2 = np.sum(dscores,axis=0) #(C,)
dh1 = dscores.dot(W2.T) #(N,H)
dW2 = h1.T.dot(dscores) + reg * W2 #(H,C)
dRelu = (h1 > 0) * dh1 #(N,H)
dW1 = X.T.dot(dRelu) + reg * W1 #(D,H)
db1 = np.sum(dRelu,axis=0) #(H,)
grads['b2'] = db2
grads['W2'] = dW2
grads['W1'] = dW1
grads['b1'] = db1
Training data
主要完成随机选择数据和对参数进行更新
neural_net.py中的train()
idx = np.random.choice(num_train,batch_size,replace=True)
X_batch = X[idx,:]
y_batch = y[idx]
self.params['W2'] += -learning_rate * grads['W2']
self.params['b2'] += -learning_rate * grads['b2']
self.params['W1'] += -learning_rate * grads['W1']
self.params['b1'] += -learning_rate * grads['b1']
predict()
scores = self.loss(X)
y_pred = np.argmax(scores, axis=1)
接下来通过自己验证来选择超参,验证步骤:
- 根据学习曲线得到该模型处于欠拟合状态,故首先调整隐藏层的大小,写一个循环对隐藏层进行循环测试。
- 根据梯度下降图像来看,学习率过低,对学习率增大并进行循环。
- 增加迭代次数
- 减小正则化参数
效果:当hidden_size=150, reg=0.09, learning_rate=1e-3时,准确率达到53.7%
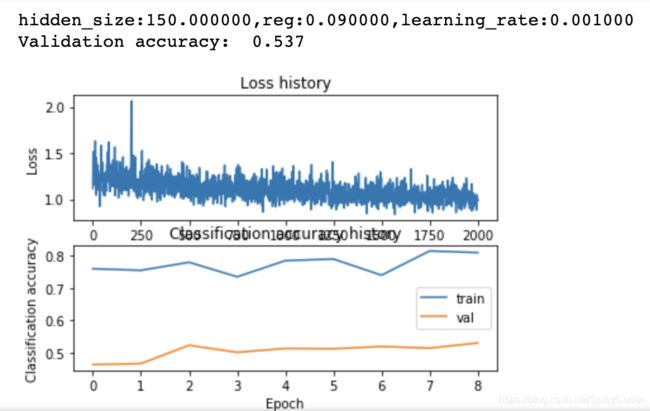
代码:
input_size = 32 * 32 * 3
hidden_size = [100,125,150]
num_classes = 10
reg = [0.03,0.05,0.09]
learing_rate = [1e-3]
best_acc = 0.40
for hs in hidden_size:
net = TwoLayerNet(input_size, hs, num_classes)
for r in reg:
for lr in learing_rate:
# Train the network
stats = net.train(X_train, y_train, X_val, y_val,
num_iters=2000, batch_size=200,
learning_rate=lr, learning_rate_decay=0.95,
reg=r, verbose=False)
# Predict on the validation set
val_acc = (net.predict(X_val) == y_val).mean()
print('hidden_size:%f,reg:%f,learning_rate:%f'%(hs,r,lr))
print('Validation accuracy: ', val_acc)
if (val_acc > best_acc):
best_acc = val_acc
best_net = net
plt.subplot(2, 1, 1)
plt.plot(stats['loss_history'])
plt.title('Loss history')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.subplot(2, 1, 2)
plt.plot(stats['train_acc_history'], label='train')
plt.plot(stats['val_acc_history'], label='val')
plt.title('Classification accuracy history')
plt.xlabel('Epoch')
plt.ylabel('Classification accuracy')
plt.legend()
plt.show()
pass
将网络中W1可视化:

最后在测试数据集上的准确率为:Test accuracy: 0.545
Inline Question
Inline Question
Now that you have trained a Neural Network classifier, you may find that your testing accuracy is much lower than the training accuracy. In what ways can we decrease this gap? Select all that apply.
- Train on a larger dataset.
- Add more hidden units.
- Increase the regularization strength.
- None of the above.
Y o u r A n s w e r : \color{blue}{\textit Your Answer:} YourAnswer:
1、2、3
Y o u r E x p l a n a t i o n : \color{blue}{\textit Your Explanation:} YourExplanation:
当间隙很大时,很可能发生了过拟合,因此增加训练集、增加隐藏层单元数、增加正则化参数都可以降低过拟合程度,从而减小间隙大小。
参考文章:
cs231n的第一次作业2层神经网络