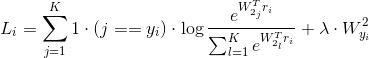CS231n 课程作业 Assignment One（五）两层神经网络分类器（0816）

两层神经网络分类器–Neural Network（2layers）

全连接神经网络、单隐藏层

一、原理

1.1 全连接神经网络

基础理论见另一篇文章–全连接神经网络

1.2 损失函数

（待完善，想看可留言）

二、实现

2.1 损失函数与求导

    def loss(self, X, y=None, reg=0.0):
        """
        Compute the loss and gradients for a two layer fully connected neural
        network.

        Inputs:
        - X: Input data of shape (N, D). Each X[i] is a training sample.
        - y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
          an integer in the range 0 <= y[i] < C. This parameter is optional; if it
          is not passed then we only return scores, and if it is passed then we
          instead return the loss and gradients.
        - reg: Regularization strength.

        Returns:
        If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
        the score for class c on input X[i].

        If y is not None, instead return a tuple of:
        - loss: Loss (data loss and regularization loss) for this batch of training
          samples.
        - grads: Dictionary mapping parameter names to gradients of those parameters
          with respect to the loss function; has the same keys as self.params.
        """
        # Unpack variables from the params dictionary
        W1, b1 = self.params['W1'], self.params['b1']
        W2, b2 = self.params['W2'], self.params['b2']
        N, D = X.shape

        # Compute the forward pass
        scores = None
        #############################################################################
        # TODO: Perform the forward pass, computing the class scores for the input. #
        # Store the result in the scores variable, which should be an array of      #
        # shape (N, C).                                                             #
        #############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        h_output = np.maximum(0,X.dot(W1)+b1) #第一层输出(N,H) relu激活
        scores = h_output.dot(W2)+b2 #第二层线性输出 (N,C) 之后接softmax
        
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # If the targets are not given then jump out, we're done
        if y is None:
            return scores

        # Compute the loss
        loss = None
        #############################################################################
        # TODO: Finish the forward pass, and compute the loss. This should include  #
        # both the data loss and L2 regularization for W1 and W2. Store the result  #
        # in the variable loss, which should be a scalar. Use the Softmax           #
        # classifier loss.                                                          #
        #############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        
        #经过softmax层计算loss
        shift_scores = scores - np.max(scores,axis=1).reshape((-1,1))
        softmax_output = np.exp(shift_scores)/np.sum(np.exp(shift_scores),axis=1).reshape(-1,1)
        loss = -np.sum(np.log(softmax_output[range(N),list(y)]))
        loss/=N
        loss+=reg*(np.sum(W1*W1)+np.sum(W2*W2))
        
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # Backward pass: compute gradients
        grads = {}
        #############################################################################
        # TODO: Compute the backward pass, computing the derivatives of the weights #
        # and biases. Store the results in the grads dictionary. For example,       #
        # grads['W1'] should store the gradient on W1, and be a matrix of same size #
        #############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        dscores = softmax_output.copy()
        dscores[range(N),list(y)]-=1
        dscores/=N
        grads['W2'] = h_output.T.dot(dscores) + 2*reg*W2
        grads['b2'] = np.sum(dscores,axis=0)

        dh = dscores.dot(W2.T)
        dh_ReLu = (h_output>0)*dh
        grads['W1'] = X.T.dot(dh_ReLu) + 2*reg*W1
        grads['b1'] = np.sum(dh_ReLu,axis = 0)
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        return loss, grads

代码分析：

关键点在于y是否为none
此函数用于计算loss，以及各个参数的梯度。就是把两个神经层以及最后一层softmax串联起来

2.2 训练过程

神经网络训练过程主要是完成以下工作：

1、接收数据，进行批处理和迭代相关参数的设置
2、喂数据，得到 loss和梯度
3、更新神经网络参数w1，w2，b1，b2
4、设置指数衰减学习率

    def train(self, X, y, X_val, y_val,
              learning_rate=1e-3, learning_rate_decay=0.95,
              reg=5e-6, num_iters=100,
              batch_size=200, verbose=False):
        """
        Train this neural network using stochastic gradient descent.

        Inputs:
        - X: A numpy array of shape (N, D) giving training data.
        - y: A numpy array f shape (N,) giving training labels; y[i] = c means that
          X[i] has label c, where 0 <= c < C.
        - X_val: A numpy array of shape (N_val, D) giving validation data.
        - y_val: A numpy array of shape (N_val,) giving validation labels.
        - learning_rate: Scalar giving learning rate for optimization.
        - learning_rate_decay: Scalar giving factor used to decay the learning rate
          after each epoch.
        - reg: Scalar giving regularization strength.
        - num_iters: Number of steps to take when optimizing.
        - batch_size: Number of training examples to use per step.
        - verbose: boolean; if true print progress during optimization.
        """
        num_train = X.shape[0]
        iterations_per_epoch = max(num_train / batch_size, 1)

        # Use SGD to optimize the parameters in self.model
        loss_history = []
        train_acc_history = []
        val_acc_history = []

        for it in range(num_iters):
            X_batch = None
            y_batch = None

            #########################################################################
            # TODO: Create a random minibatch of training data and labels, storing  #
            # them in X_batch and y_batch respectively.                             #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            idx = np.random.choice(num_train,batch_size,replace =True)
            X_batch = X[idx]
            y_batch = y[idx]
            
            pass

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            # Compute loss and gradients using the current minibatch
            loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
            loss_history.append(loss)

            #########################################################################
            # TODO: Use the gradients in the grads dictionary to update the         #
            # parameters of the network (stored in the dictionary self.params)      #
            # using stochastic gradient descent. You'll need to use the gradients   #
            # stored in the grads dictionary defined above.                         #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            self.params['W2'] += -learning_rate * grads['W2']
            self.params['b2'] += -learning_rate * grads['b2']
            self.params['W1'] += -learning_rate * grads['W1']
            self.params['b1'] += -learning_rate * grads['b1']
            
            pass

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            if verbose and it % 100 == 0:
                print('iteration %d / %d: loss %f' % (it, num_iters, loss))

            # Every epoch, check train and val accuracy and decay learning rate.
            if it % iterations_per_epoch == 0:
                # Check accuracy
                train_acc = (self.predict(X_batch) == y_batch).mean()
                val_acc = (self.predict(X_val) == y_val).mean()
                train_acc_history.append(train_acc)
                val_acc_history.append(val_acc)

                # Decay learning rate
                learning_rate *= learning_rate_decay

        return {
          'loss_history': loss_history,
          'train_acc_history': train_acc_history,
          'val_acc_history': val_acc_history,
        }

2.3 预测部分

输入数据，计算一轮前向通道，得到输出标签

   def predict(self, X):
        """
        Use the trained weights of this two-layer network to predict labels for
        data points. For each data point we predict scores for each of the C
        classes, and assign each data point to the class with the highest score.

        Inputs:
        - X: A numpy array of shape (N, D) giving N D-dimensional data points to
          classify.

        Returns:
        - y_pred: A numpy array of shape (N,) giving predicted labels for each of
          the elements of X. For all i, y_pred[i] = c means that X[i] is predicted
          to have class c, where 0 <= c < C.
        """
        y_pred = None

        ###########################################################################
        # TODO: Implement this function; it should be VERY simple!                #
        ###########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        h = np.maximum(0,X.dot(self.params['W1'])+self.params['b1'])
        scores = h.dot(self.params['W2'])+self.params['b2']
        y_pred = np.argmax(scores,axis=1)
        
        pass

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        return y_pred

三、调用分类器进行图片分类

3.1 Forward pass: compute scores

scores = net.loss(X)
print('Your scores:')
print(scores)
print()
print('correct scores:')
correct_scores = np.asarray([
  [-0.81233741, -1.27654624, -0.70335995],
  [-0.17129677, -1.18803311, -0.47310444],
  [-0.51590475, -1.01354314, -0.8504215 ],
  [-0.15419291, -0.48629638, -0.52901952],
  [-0.00618733, -0.12435261, -0.15226949]])
print(correct_scores)
print()

# The difference should be very small. We get < 1e-7
print('Difference between your scores and correct scores:')
print(np.sum(np.abs(scores - correct_scores)))

输出：

Your scores:
[[-0.81233741 -1.27654624 -0.70335995]
 [-0.17129677 -1.18803311 -0.47310444]
 [-0.51590475 -1.01354314 -0.8504215 ]
 [-0.15419291 -0.48629638 -0.52901952]
 [-0.00618733 -0.12435261 -0.15226949]]

correct scores:
[[-0.81233741 -1.27654624 -0.70335995]
 [-0.17129677 -1.18803311 -0.47310444]
 [-0.51590475 -1.01354314 -0.8504215 ]
 [-0.15419291 -0.48629638 -0.52901952]
 [-0.00618733 -0.12435261 -0.15226949]]

Difference between your scores and correct scores:
3.6802720745909845e-08

3.2 Forward pass: compute loss

loss, _ = net.loss(X, y, reg=0.05)
correct_loss = 1.30378789133

# should be very small, we get < 1e-12
print('Difference between your loss and correct loss:')
print(np.sum(np.abs(loss - correct_loss)))

输出：

Difference between your loss and correct loss:
1.7985612998927536e-13

3.3 Backward pass

This will compute the gradient of the loss with respect to the variables W1, b1, W2, and b2. Now that you (hopefully!) have a correctly implemented forward pass, you can debug your backward pass using a numeric gradient check:

from cs231n.gradient_check import eval_numerical_gradient

# Use numeric gradient checking to check your implementation of the backward pass.
# If your implementation is correct, the difference between the numeric and
# analytic gradients should be less than 1e-8 for each of W1, W2, b1, and b2.

loss, grads = net.loss(X, y, reg=0.05)

# these should all be less than 1e-8 or so
for param_name in grads:
    f = lambda W: net.loss(X, y, reg=0.05)[0]
    param_grad_num = eval_numerical_gradient(f, net.params[param_name], verbose=False)
    print('%s max relative error: %e' % (param_name, rel_error(param_grad_num, grads[param_name])))

输出：

W2 max relative error: 3.440708e-09
b2 max relative error: 4.447625e-11
W1 max relative error: 3.561318e-09
b1 max relative error: 2.738421e-09

3.4 Train the network

To train the network we will use stochastic gradient descent (SGD), similar to the SVM and Softmax classifiers. Look at the function TwoLayerNet.train and fill in the missing sections to implement the training procedure. This should be very similar to the training procedure you used for the SVM and Softmax classifiers. You will also have to implement TwoLayerNet.predict, as the training process periodically performs prediction to keep track of accuracy over time while the network trains.

Once you have implemented the method, run the code below to train a two-layer network on toy data. You should achieve a training loss less than 0.02.

net = init_toy_model()
stats = net.train(X, y, X, y,
            learning_rate=1e-1, reg=5e-6,
            num_iters=100, verbose=False)

print('Final training loss: ', stats['loss_history'][-1])

# plot the loss history
plt.plot(stats['loss_history'])
plt.xlabel('iteration')
plt.ylabel('training loss')
plt.title('Training Loss history')
plt.show()

输出：Final training loss: 0.017149607938732093

3.5 Load the data

from cs231n.data_utils import load_CIFAR10

def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000):
    """
    Load the CIFAR-10 dataset from disk and perform preprocessing to prepare
    it for the two-layer neural net classifier. These are the same steps as
    we used for the SVM, but condensed to a single function.  
    """
    # Load the raw CIFAR-10 data
    cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
    
    # Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
    try:
       del X_train, y_train
       del X_test, y_test
       print('Clear previously loaded data.')
    except:
       pass

    X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
        
    # Subsample the data
    mask = list(range(num_training, num_training + num_validation))
    X_val = X_train[mask]
    y_val = y_train[mask]
    mask = list(range(num_training))
    X_train = X_train[mask]
    y_train = y_train[mask]
    mask = list(range(num_test))
    X_test = X_test[mask]
    y_test = y_test[mask]

    # Normalize the data: subtract the mean image
    mean_image = np.mean(X_train, axis=0)
    X_train -= mean_image
    X_val -= mean_image
    X_test -= mean_image

    # Reshape data to rows
    X_train = X_train.reshape(num_training, -1)
    X_val = X_val.reshape(num_validation, -1)
    X_test = X_test.reshape(num_test, -1)

    return X_train, y_train, X_val, y_val, X_test, y_test


# Invoke the above function to get our data.
X_train, y_train, X_val, y_val, X_test, y_test = get_CIFAR10_data()
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)

输出：

Train data shape:  (49000, 3072)
Train labels shape:  (49000,)
Validation data shape:  (1000, 3072)
Validation labels shape:  (1000,)
Test data shape:  (1000, 3072)
Test labels shape:  (1000,)

3.6 Train a network

input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
net = TwoLayerNet(input_size, hidden_size, num_classes)

# Train the network
stats = net.train(X_train, y_train, X_val, y_val,
            num_iters=1000, batch_size=200,
            learning_rate=1e-4, learning_rate_decay=0.95,
            reg=0.25, verbose=True)

# Predict on the validation set
val_acc = (net.predict(X_val) == y_val).mean()
print('Validation accuracy: ', val_acc)

输出：

iteration 0 / 1000: loss 2.302954
iteration 100 / 1000: loss 2.302550
iteration 200 / 1000: loss 2.297648
iteration 300 / 1000: loss 2.259602
iteration 400 / 1000: loss 2.204170
iteration 500 / 1000: loss 2.118565
iteration 600 / 1000: loss 2.051535
iteration 700 / 1000: loss 1.988466
iteration 800 / 1000: loss 2.006591
iteration 900 / 1000: loss 1.951473
Validation accuracy:  0.287

3.7 Debug the training

With the default parameters we provided above, you should get a validation accuracy of about 0.29 on the validation set. This isn’t very good.

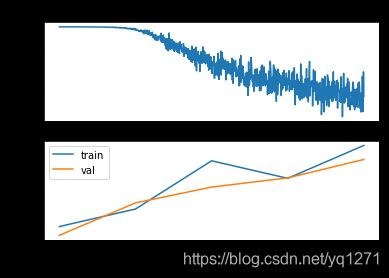
One strategy for getting insight into what’s wrong is to plot the loss function and the accuracies on the training and validation sets during optimization.

Another strategy is to visualize the weights that were learned in the first layer of the network. In most neural networks trained on visual data, the first layer weights typically show some visible structure when visualized.

# Plot the loss function and train / validation accuracies
plt.subplot(2, 1, 1)
plt.plot(stats['loss_history'])
plt.title('Loss history')
plt.xlabel('Iteration')
plt.ylabel('Loss')

plt.subplot(2, 1, 2)
plt.plot(stats['train_acc_history'], label='train')
plt.plot(stats['val_acc_history'], label='val')
plt.title('Classification accuracy history')
plt.xlabel('Epoch')
plt.ylabel('Classification accuracy')
plt.legend()
plt.show()

权重矩阵可视化

from cs231n.vis_utils import visualize_grid

# Visualize the weights of the network

def show_net_weights(net):
    W1 = net.params['W1']
    W1 = W1.reshape(32, 32, 3, -1).transpose(3, 0, 1, 2)
    plt.imshow(visualize_grid(W1, padding=3).astype('uint8'))
    plt.gca().axis('off')
    plt.show()

show_net_weights(net)

3.8 Tune your hyperparameters

What’s wrong?. Looking at the visualizations above, we see that the loss is decreasing more or less linearly, which seems to suggest that the learning rate may be too low. Moreover, there is no gap between the training and validation accuracy, suggesting that the model we used has low capacity, and that we should increase its size. On the other hand, with a very large model we would expect to see more overfitting, which would manifest itself as a very large gap between the training and validation accuracy.

Tuning. Tuning the hyperparameters and developing intuition for how they affect the final performance is a large part of using Neural Networks, so we want you to get a lot of practice. Below, you should experiment with different values of the various hyperparameters, including hidden layer size, learning rate, numer of training epochs, and regularization strength. You might also consider tuning the learning rate decay, but you should be able to get good performance using the default value.

Approximate results. You should be aim to achieve a classification accuracy of greater than 48% on the validation set. Our best network gets over 52% on the validation set.

Experiment: You goal in this exercise is to get as good of a result on CIFAR-10 as you can (52% could serve as a reference), with a fully-connected Neural Network. Feel free implement your own techniques (e.g. PCA to reduce dimensionality, or adding dropout, or adding features to the solver, etc.).

best_net = None # store the best model into this 

#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained  #
# model in best_net.                                                            #
#                                                                               #
# To help debug your network, it may help to use visualizations similar to the  #
# ones we used above; these visualizations will have significant qualitative    #
# differences from the ones we saw above for the poorly tuned network.          #
#                                                                               #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
# write code to sweep through possible combinations of hyperparameters          #
# automatically like we did on the previous exercises.                          #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
results = {}
best_val = -1
learning_rates = [1e-3, 1.2e-3, 1.75e-3]
regularization_strengths = [1, 1.25, 1.5]

for lr in learning_rates:
    for reg in regularization_strengths:
        net = TwoLayerNet(input_size, hidden_size, num_classes)
        loss_hist = net.train(X_train, y_train, X_val, y_val,
                    num_iters=2000, batch_size=200,
                    learning_rate=lr, learning_rate_decay=0.95,
                    reg=reg, verbose=False)
        y_train_pred = net.predict(X_train)
        y_val_pred = net.predict(X_val)
        y_train_acc = np.mean(y_train_pred==y_train)
        y_val_acc = np.mean(y_val_pred==y_val)
        results[(lr,reg)] = [y_train_acc, y_val_acc]
        if y_val_acc > best_val:
            best_val = y_val_acc
            best_net = net
for lr, reg in sorted(results):
    train_accuracy, val_accuracy = results[(lr, reg)]
    print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
                lr, reg, train_accuracy, val_accuracy))
    
print('best validation accuracy achieved during cross-validation: %f' % best_val)
pass

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

输出：

lr 1.000000e-03 reg 1.000000e+00 train accuracy: 0.494939 val accuracy: 0.477000
lr 1.000000e-03 reg 1.250000e+00 train accuracy: 0.481837 val accuracy: 0.472000
lr 1.000000e-03 reg 1.500000e+00 train accuracy: 0.474061 val accuracy: 0.458000
lr 1.200000e-03 reg 1.000000e+00 train accuracy: 0.496939 val accuracy: 0.469000
lr 1.200000e-03 reg 1.250000e+00 train accuracy: 0.465755 val accuracy: 0.464000
lr 1.200000e-03 reg 1.500000e+00 train accuracy: 0.470939 val accuracy: 0.455000
lr 1.750000e-03 reg 1.000000e+00 train accuracy: 0.475673 val accuracy: 0.449000
lr 1.750000e-03 reg 1.250000e+00 train accuracy: 0.474204 val accuracy: 0.455000
lr 1.750000e-03 reg 1.500000e+00 train accuracy: 0.464551 val accuracy: 0.464000
best validation accuracy achieved during cross-validation: 0.477000

调用最佳参数

# Print your validation accuracy: this should be above 48%
val_acc = (best_net.predict(X_val) == y_val).mean()
print('Validation accuracy: ', val_acc)

# Visualize the weights of the best network
show_net_weights(best_net)

输出：Validation accuracy: 0.477

3.9 Run on the test set

# Print your test accuracy: this should be above 48%
test_acc = (best_net.predict(X_test) == y_test).mean()
print('Test accuracy: ', test_acc)

输出：Test accuracy: 0.5

四、问题

Inline Question

提问：Now that you have trained a Neural Network classifier, you may find that your testing accuracy is much lower than the training accuracy. In what ways can we decrease this gap? Select all that apply.
1.Train on a larger dataset.
2.Add more hidden units.
3.Increase the regularization strength.
4.None of the above.

翻译：既然您已经训练了神经网络分类器，您可能会发现测试精度远低于训练精度。 我们可以通过哪些方式缩小这一差距？ 选择所有符合条件的。
1.训练更大的数据集
2.添加更多隐藏单位。
3.增加正则强度。
4.以上都不是。

回答：1.2