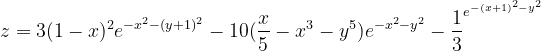遗传算法及python实现
目录
一、遗传算法概念
二、遗传算法应用实例
基础概念:
1、种群和个体:
2、编码、解码与染色体:
3、适应度和选择:
4、 交叉、变异:
三、遗传算法python完整代码
“适者生存,不适者淘汰”
一、遗传算法概念
用于解决最优化问题的一种搜索算法
(1)具有相同或类似的功能的算法:
- 粒子群算法(PSO)
- 退火算法
- 蚁群算法
(2)常用场景:求解目标函数的最大值或者最小值问题
二、遗传算法应用实例
目标函数:
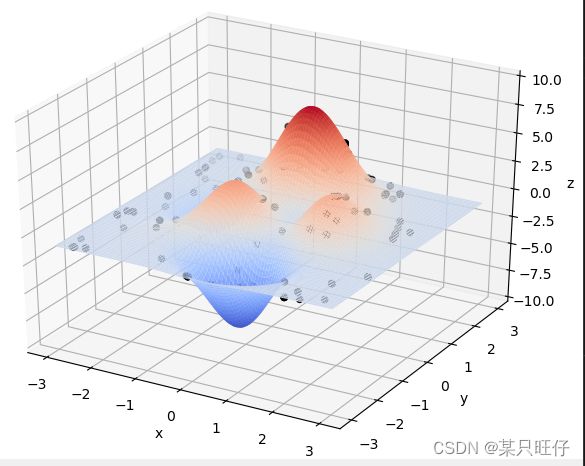
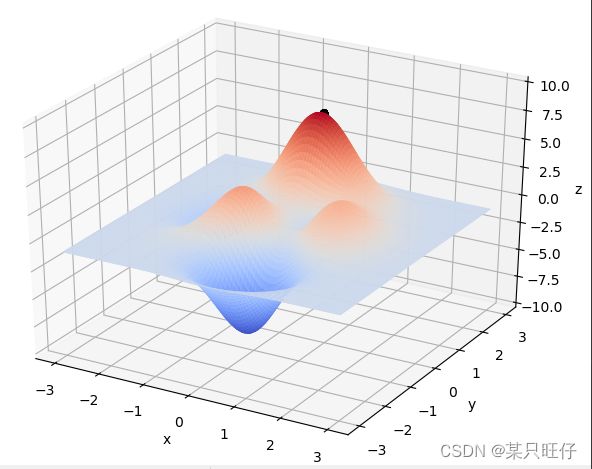
函数图像:
基础概念:
1、种群和个体:
在遗传算法里,个体通常为某个问题的一个解,并且该解在计算机中被编码为一个向量表示
在该例子中,问题的一个可能解的通用形式为(x,y),例如(0,1),(2,3)......而这一组组可能解组成的集合叫作种群。
2、编码、解码与染色体:
- 编码:将一组可能解编码成一个向量,即我们将不同的实数转化成不同的0,1二进制串表示,其中保持某种映射关系
 。考虑到遗传算法的程序中,我们首先是对二进制串进行操作的,而不是先随机生成十进制数再编码的,因此我们无需知道具体的映射关系。
。考虑到遗传算法的程序中,我们首先是对二进制串进行操作的,而不是先随机生成十进制数再编码的,因此我们无需知道具体的映射关系。 - 解码:将编码后的二进制串转换成十进制串,也就是需要y=f(x)的逆映射。
1. 将二进制码按权展开,转化成十进制数
例如:二进制码为 [1 1 0 1 0] ,转化成十进制数为 ![]()
2. 将转化的十进制数压缩到[0,1]之间的小数
3. 将这个小数映射到我们所需要的区间内
例如:我们此时函数中x的取值范围为[-3,3],y的取值范围为[-3,3]
![]()
![]()
通用公式:num为2步得到的小数,![]() 为x的上限,
为x的上限,![]() 为x的下限,
为x的下限,![]() 为y的上限, ,
为y的上限, ,![]() 为y的下限
为y的下限
![]()
![]()
3、适应度和选择:
我们在求最大值的问题中可以直接用可能解(个体)对应的函数的函数值的大小来评估,这样可能解对应的函数值越大越有可能被保留下来。在求最小值问题上,函数值越小的可能解对应的适应度应该越大,同时适应度也不能为负值,先将适应度减去最大预测值,将适应度可能取值区间压缩为 [ n p . m i n ( p r e d ) − n p . m a x ( p r e d ) , 0 ] [np.min(pred)-np.max(pred), 0] [np.min(pred)−np.max(pred),0],然后添加个负号将适应度变为正数,同理为了不出现0,最后在加上一个很小的正数。
#求解函数最大值
def get_fitness(pop):
x,y = translateDNA(pop) #解码过程
pred = F(x, y) #代入原函数求解适应度
return (pred - np.min(pred)) + 1e-3 #减去最小的适应度是为了防止适应度出现负数,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度
#求解函数最小值
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return -(pred - np.max(pred)) + 1e-3
选择时的原则: 适应度越高,被选择的机会越高,而适应度低的,被选择的机会就低。而不是完全以适应度高低为导向,否则容易陷入局部最优解。
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness)/(fitness.sum()) )
return pop[idx]
4、 交叉、变异:
交叉是指每一个个体是由父亲和母亲两个个体繁殖产生,子代个体的DNA(二进制串)获得了一半父亲的DNA,一半母亲的DNA,但是这里的一半并不是真正的一半,这个位置叫做交配点,是随机产生的,可以是染色体的任意位置。通过交叉子代获得了一半来自父亲一半来自母亲的DNA,但是子代自身可能发生变异,使得其DNA即不来自父亲,也不来自母亲,在某个位置上发生随机改变,通常就是改变DNA的一个二进制位(0变到1,或者1变到0)。
找交配片段的方法:对DNA进行剪接,找到两处随机点位置,对中间的片段进行交叉操作。
交叉概率,范围一般是0.6~1,突变常数(又称为变异概率),通常是0.1或者更小。
#交叉
def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
new_pop = []
for father in pop: #遍历种群中的每一个个体,将该个体作为父亲
child = father #孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: #产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] #再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE*2) #随机产生交叉的点
child[cross_points:] = mother[cross_points:] #孩子得到位于交叉点后的母亲的基因
mutation(child) #每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
#变异
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: #以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE) #随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point]^1 #将变异点的二进制为反转
三、遗传算法python完整代码
转载:遗传算法详解 附python代码实现_重学CS的博客-CSDN博客_python遗传算法
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
DNA_SIZE = 24
POP_SIZE = 200
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 50
X_BOUND = [-3, 3]
Y_BOUND = [-3, 3]
def F(x, y):
return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X,Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
ax.set_zlim(-10,10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return (pred - np.min(pred)) + 1e-3 #减去最小的适应度是为了防止适应度出现负数,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度
def translateDNA(pop): #pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:,1::2]#奇数列表示X
y_pop = pop[:,::2] #偶数列表示y
#pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
return x,y
def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
new_pop = []
for father in pop: #遍历种群中的每一个个体,将该个体作为父亲
child = father #孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: #产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] #再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE*2) #随机产生交叉的点
child[cross_points:] = mother[cross_points:] #孩子得到位于交叉点后的母亲的基因
mutation(child) #每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: #以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE*2) #随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point]^1 #将变异点的二进制为反转
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness)/(fitness.sum()) )
return pop[idx]
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x,y = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
if __name__ == "__main__":
fig = plt.figure()
ax = Axes3D(fig)
plt.ion()#将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_3d(ax)
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS):#迭代N代
x,y = translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x, y, F(x,y), c='black', marker='o');plt.show();plt.pause(0.1)
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
#F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
fitness = get_fitness(pop)
pop = select(pop, fitness) #选择生成新的种群
print_info(pop)
plt.ioff()
plot_3d(ax)
在Visual Studio Code中运行结果如下:
- max_fitness: 0.001246770880719005
- 最优的基因型: [1 1 0 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 0 1
0 0 1 0 1 0 0 1 1 1 1]
- (x, y): (0.09614021159054165, 1.4999898970121084)