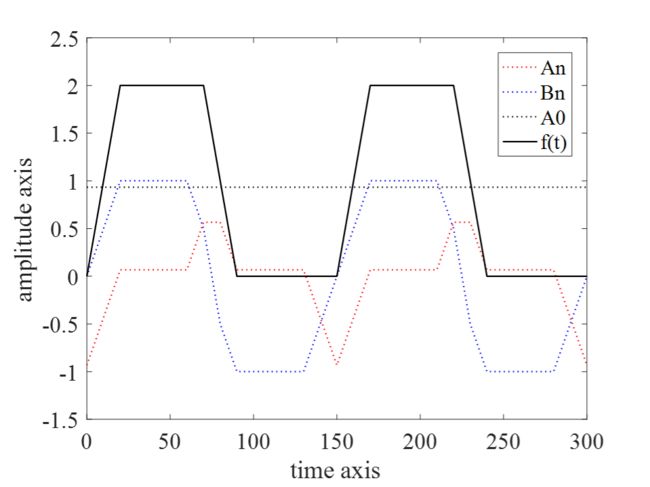
梯形波的傅里叶级数分解
文章目录
- 1.前言
- 2.动手开搞
- 3.导入matlab 进行plot
-
- 3.1 A=1,T=100,m=10,h=30,p=20
- 3.2 A=1,T=100,m=5,h=40,p=5
- 3.3 A=2,T=150,m=20,h=50,p=1
- 3.4 奇偶对称性
- 4.代码
1.前言
想必大家搜索看到这篇文章的时候,大概已经是踏入信号与系统的大门,不满足于书上的简单的矩形波三角波,想探探梯形波,今天它来了~
信号一定是让你可以在硬件领域有提升的一门课程!请大家放心。
今天有点忙,上午办事,下午要睡觉,晚上要做一个题目,周五是在徘徊犹豫的边缘,这题做不做,这题搞一下一定是要3-4个小时左右。
事情起因这样:
前几天在CSDN 硬件工程师炼成之路 大佬 的一篇文章《不同的反射系数,信号的是怎样的呢?》写的很好,里面大概是讲了源端发射到终端,用信号反射的观点,去计算源端和终端的电压波形。
用的是梯形波:
因为实际的TX端,边沿不可能无限陡峭,脉宽也要做成可控。这个波形比单纯的矩形波更常用。
傅里叶级数真的优雅,一般书本上的习题也都是三角波、矩形波,积分起来相对容易。脑子里突然一热,想把边沿可变+脉宽可控的梯形波,用傅里叶级数分解掉。

有点飘了,数学底子不行,不会用对称性,积分也不熟练了,没什么技巧,就是死做。
2.动手开搞
周五晚上就酝酿了,徘徊退缩了很久想一想还是积一下,网上仅有的资源也几乎只有一个答案,而且边沿不灵活,数学表达式也不是我想要的。
列表达式:

然后开始漫长的积分,很长很长,很细很细,像是高中的笨小孩,死做椭圆的题,设未知数,代入方程越解越长:
过程非常的痛苦,实不相瞒持续了3个小时,输完所有公式,从18.30持续纠错到近了22.30,洋洋洒洒7-8页的重复劳动。
*所有详细的推导放在网盘里了
3.导入matlab 进行plot
matlab是个高级计算器了,可以帮你验证下积分的结果正确与否。
把word里的公式全部打入 matlab文件,看看波图
3.1 A=1,T=100,m=10,h=30,p=20
(1)振幅A=1,周期T=100,上升时间m=10,正脉宽=30,下降时间p=20;
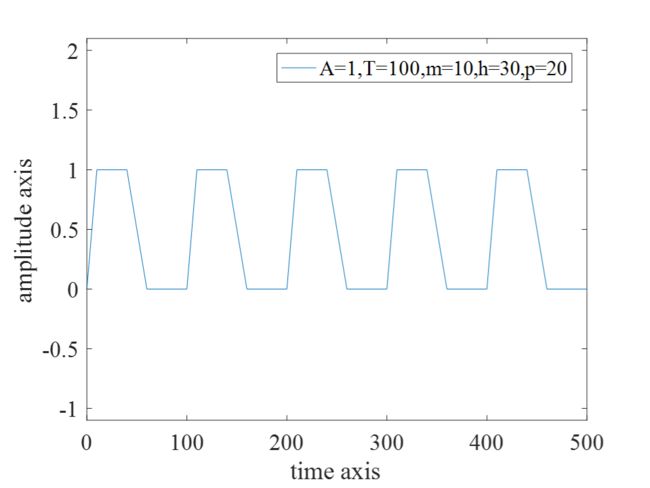
3.2 A=1,T=100,m=5,h=40,p=5
(2)振幅A=1,周期T=100,上升时间m=5,正脉宽=40,下降时间p=5;
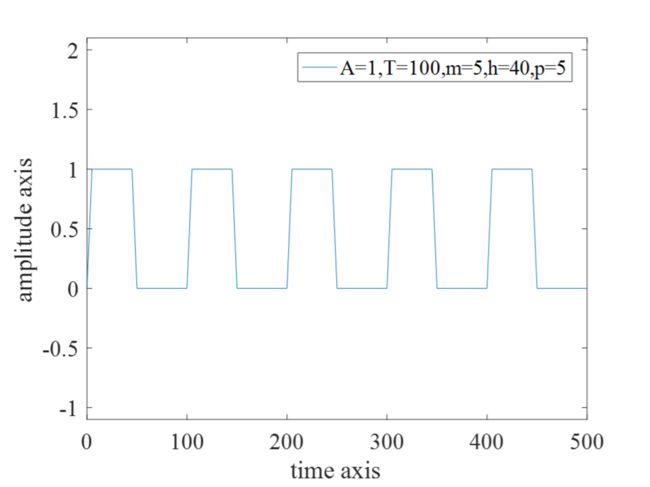
3.3 A=2,T=150,m=20,h=50,p=1
(3)振幅A=2,周期T=150,上升时间m=20,正脉宽=50,下降时间p=1;
3.4 奇偶对称性

可以看到An是偶函数,Bn是奇函数,A0是f(t)的直流分量。
波形非常的完美,不过无法想象,为什么要在那些点跳变,把这三个值相加就正好是一个梯形波。
4.代码
clear all;
close all;
%parameter set
n=1:1:10;
A=2;T=150;m=20;h=50;p=20;
t=0:0.01:2*T;
str=strcat('A=',num2str(A),',T=',num2str(T),',m=', ...
num2str(m),',h=',num2str(h),',p=',num2str(p) )
%(2./T)
%n.*omg
omg=2.*pi./T;
%(n.*omg)
% A./(n.*omg)
g1 =(1./(n.*omg));
X1= (A./(n.*omg)).*sin(n.*omg.*m) + ...
(A./m).*( 1./ ( (n.*omg).*(n.*omg) ) ).*cos(n.*omg.*m)- ...
(A./m).*( 1./ ( (n.*omg).*(n.*omg) ) );
X2=(A./(n.*omg)).*sin(n.*omg.*m+n.*omg.*h) - ...
(A./(n.*omg)).*sin(n.*omg.*m);
% v1 (A./p).*(1./(n.*omg))
v1 = (A./p).*(1./(n.*omg));
X3_1= -v1.*(m+h+p) .* sin(n.*omg.*m+n.*omg.*h+n.*omg.*p) + ...
v1 .*(m+h).*sin(n.*omg.*m+n.*omg.*h) + ...
-v1.*g1.*cos(n.*omg.*m+n.*omg.*h+n.*omg.*p) + ...
v1.*g1.*cos(n.*omg.*m+n.*omg.*h);
v2 =(A.*m)./(p.*n.*omg);
X3_2 = v2 .* sin(n.*omg.*m+n.*omg.*h+n.*omg.*p) - ...
v2 .* sin(n.*omg.*m+n.*omg.*h);
v3 = (A)./ (n.*omg);
X3_3=v3 .* sin(n.*omg.*m+n.*omg.*h+n.*omg.*p) - ...
v3 .* sin(n.*omg.*m+n.*omg.*h);
v4 =(A.*h)./(p.*n.*omg);
X3_4 = v4 .* sin(n.*omg.*m+n.*omg.*h+n.*omg.*p) - ...
v4 .* sin(n.*omg.*m+n.*omg.*h);
X3=X3_1 + X3_2 + X3_3 + X3_4;
an=(2./T).*X1+(2./T).*X2+(2./T).*X3;
%
K1=(-A.*g1) .*cos(n.*omg.*m)+ (A./m).*g1.*g1.*sin(n.*omg.*m);
K2= -A.*g1 .* cos(n.*omg.*m + n.*omg.*h) + A.*g1.* cos(n.*omg.*m);
g2=(A./p);
K3_1=g2.*g1.*(m+h+p).*cos(n.*omg.*m + n.*omg.*h+n.*omg.*p) - ...
g2.*g1.*(m+h).*cos(n.*omg.*m + n.*omg.*h) - ...
g2.*g1.*g1.*sin(n.*omg.*m + n.*omg.*h+n.*omg.*p) + ...
g2.*g1.*g1.*sin(n.*omg.*m + n.*omg.*h);
g3=(A.*m)./(p.*n.*omg);
K3_2 = -g3.*cos(n.*omg.*m + n.*omg.*h+n.*omg.*p) + ...
g3.*cos(n.*omg.*m + n.*omg.*h) ;
K3_3 = -A.*g1.*cos(n.*omg.*m + n.*omg.*h+n.*omg.*p) + ...
A.*g1.*cos(n.*omg.*m + n.*omg.*h);
g4 = (A.*h)./(p.*n.*omg);
K3_4 = -g4.* cos(n.*omg.*m + n.*omg.*h+n.*omg.*p) + ...
+g4.* cos(n.*omg.*m + n.*omg.*h);
K3=K3_1 + K3_2 + K3_3 + K3_4;
bn=(2./T).*K1+(2./T).*K2+(2./T).*K3;
ft=zeros(1,length(t));
A0= A.*m./(2.*T) + ...
A.*h./T + ...
-(A./(2.*T.*p)) .* ( (m+h+p).* (m+h+p) -(m+h).*(m+h) ) +...
(1./T) .* (A.*m./p + A +A.*h./p ) .*p ;
for j =1:1:n(end)
ft=ft + an(j) .* cos(j.*omg.*t) + bn(j) .* sin(j.*omg.*t);
end
figure(1)
plot(t, A0 + ft)
m_max= max(A0 + ft);
m_min= min(A0 + ft);
axis([0,t(end) m_min-1.1 m_max+1.1])
legend(str)
xlabel('time axis')
ylabel('amplitude axis')
set(gca,'Fontname','Times New Roman','FontSize',15);
if 0
figure(2)
AN=zeros(1,length(t));
BN=zeros(1,length(t));
for j =1:1:n(end)
AN=AN + an(j) .* cos(j.*omg.*t);
end
for j =1:1:n(end)
BN=BN + bn(j) .* sin(j.*omg.*t);
end
plot(t, AN,':r','Linewidth',1);
hold on;
plot(t, BN,':b','Linewidth',1);
hold on;
plot(t, A0.*ones(1,length(t)),':k','Linewidth',1);
hold on;
plot(t, A0+BN+AN,'-k','Linewidth',1);
hold on;
legend('An','Bn','A0','f(t)');
xlabel('time axis')
ylabel('amplitude axis')
set(gca,'Fontname','Times New Roman','FontSize',15);
end
% + bn(j) .* sin(j.*omg.*t)
完整的文档放在网盘自取:
链接:https://pan.baidu.com/s/1kHA5rh2I8Fx54K3No3O79Q?pwd=AAAA
提取码:AAAA
欢迎关注我的公众号:沈土豪的书屋