GAMES 202 - 学习笔记（03）

GAMES 202 - 学习笔记（03）

原课程视频链接以及官网
b站视频链接: https://www.bilibili.com/video/av887241709/.
课程官网链接: https://sites.cs.ucsb.edu/~lingqi/teaching/games202.html.

上节课遗留的微积分部分课程不会再单独进行复习了，转而在每一节涉及到微积分的地方再进行解释，课程接下来会先主要介绍 Real-Time Shadows 这个话题

Real-Time Shadows

Recap: Shadow Mapping

课程首先回顾了 Shadow Mapping 的原理以及存在的问题和解决方案。

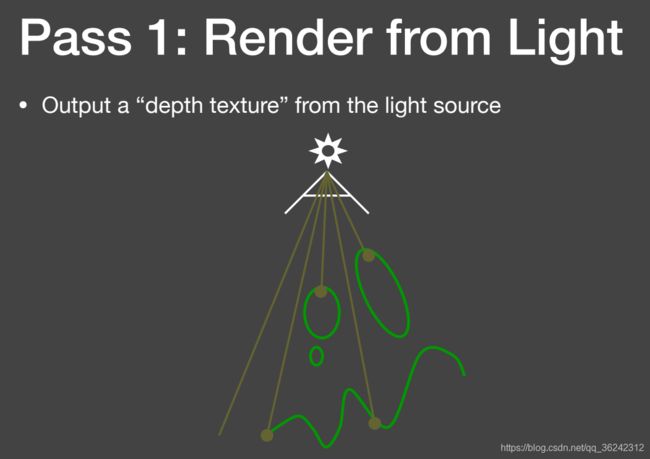
Shadow Mapping 是针对点光源制作阴影的技术。它是两趟（2-pass） 的算法：

1. 第一趟从光源出发，记录从光源看向场景的深度 $D_l$
   

2. 第二趟从实际相机位置出发，看向场景，在着色过程中查看每个点能否被光源照亮，即比较 $D_v<D_l$，注意此时 $D_v,D_l$ 应处于同一空间
   

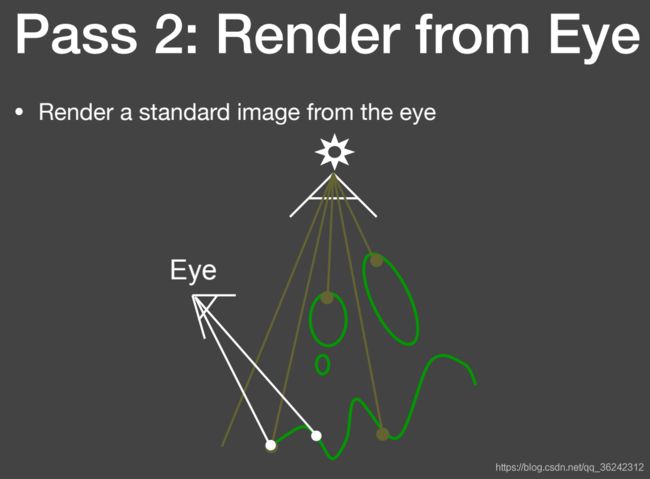
它是图像空间算法，因为需要知道的是光源到场景的深度就可以做 Shadow Mapping，它也存在一些问题，比如自遮挡和走样问题


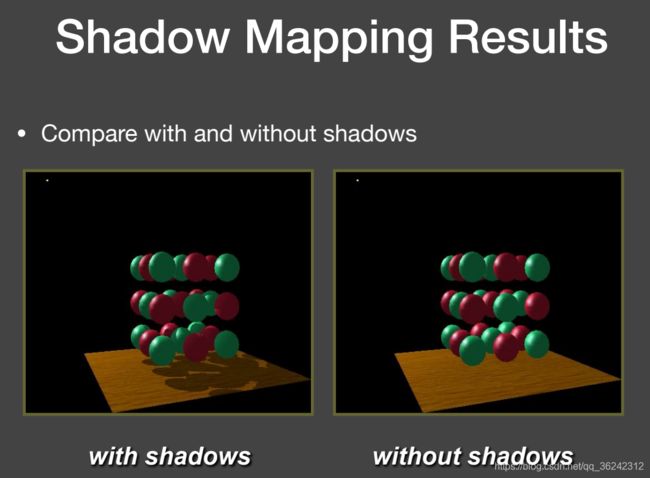
通过在 Shadow Mapping 的两趟中，对光源处所获得的深度进行可视化，可以得到如下结果：


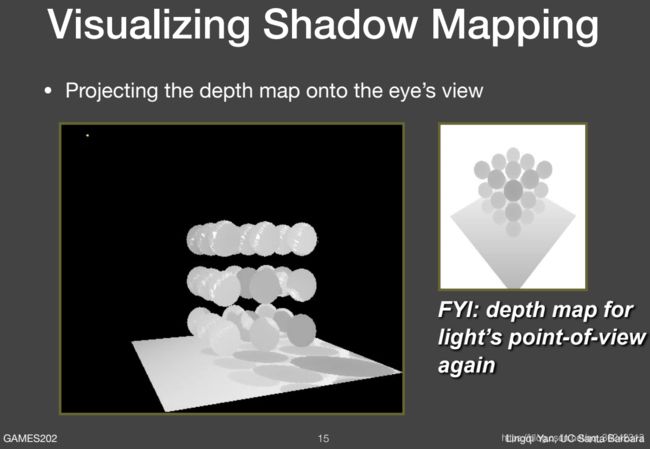
Shadow Mapping 存在的问题：

自遮挡（Self occlusion）: 是由于深度精度问题导致的。由于从光源处看向场景，会把场景的一块区域（图中红色线段区域）离散成光源处成像平面的像素，这时再与之比较，很有可能发生自遮挡问题：

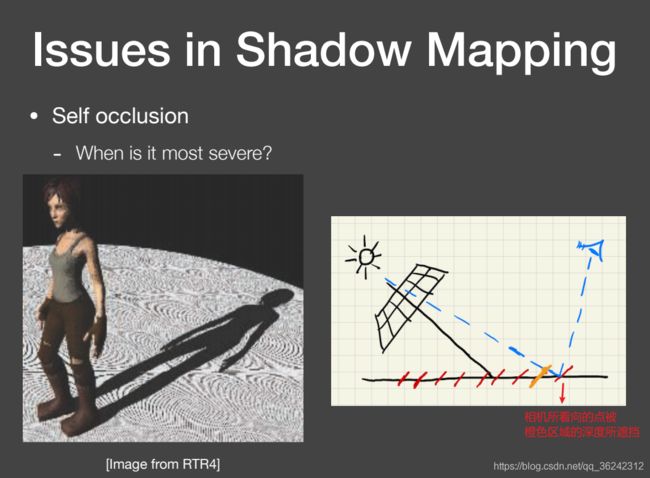
解决办法是，两趟的比较结果在一定范围内不计算阴影，添加一定的 bias，但是这同样会引来其他问题，即阴影出现断裂：

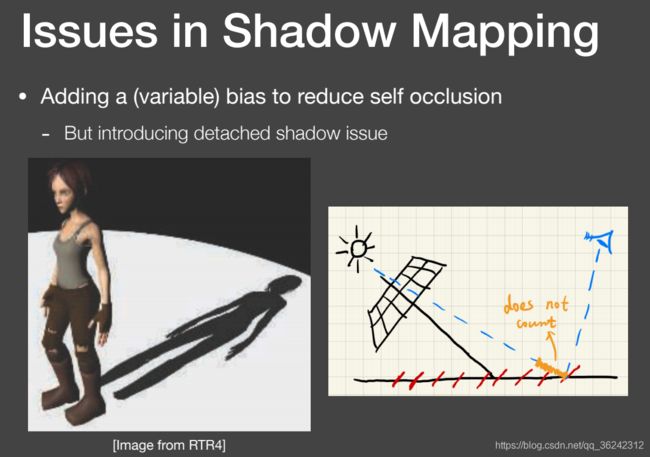
学术界也提出方法来解决这个问题，但是由于实现多了一些复杂计算和存储，所以没有得到广泛的应用：

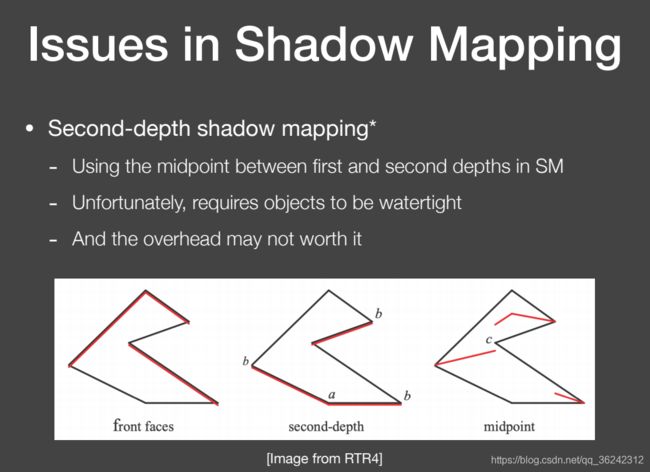
走样问题：由于深度缓冲分辨率导致的，可以采用 Cascaded Shadow Maps （该方法提供了不同分辨率的深度纹理）等方法来解决

The math behind shadow mapping

课程接下来讲了一下 Shadow Mapping 背后的数学原理：

首先在实时渲染（RTR）中，我们都考虑不等式为近似相等。在实时渲染中，有一个重要的近似为：
$${\int }_{\Omega }f(x)g(x)\mathrm{d}x\approx \frac{{\int }_{\Omega }f(x)\mathrm{d}x}{{\int }_{\Omega }\mathrm{d}x}\cdot {\int }_{\Omega }g(x)\mathrm{d}x$$

该近似何时较为准确？当：

①Small support （积分域较小）时
②$g(x)$ 较为平滑时

近似结果较为准确

考虑上一节课所说渲染方程，我们可以将它通过上述近似方法表示为：
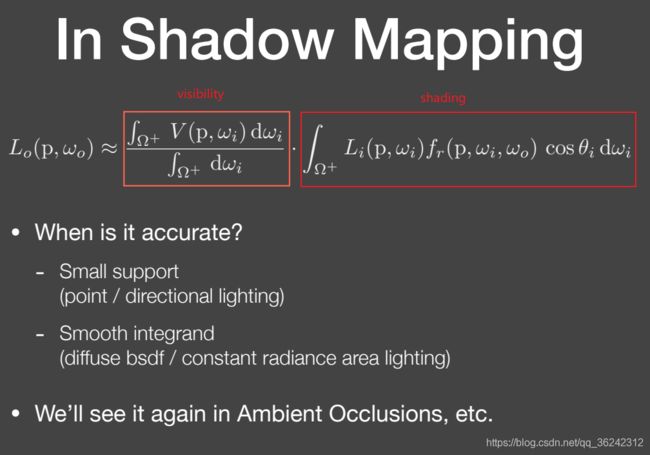
$$L_o\left(\mathrm{p},{\omega }_o\right)\approx \frac{{\int }_{{\Omega }^{+}}V\left(\mathrm{p},{\omega }_i\right)\mathrm{d}{\omega }_i}{{\int }_{{\Omega }^{+}}\mathrm{d}{\omega }_i}\cdot {\int }_{{\Omega }^{+}}{L}_i\left(\mathrm{p},{\omega }_i\right)f_r\left(\mathrm{p},{\omega }_i,{\omega }_o\right)\cos {\theta }_i\mathrm{d}{\omega }_i$$

第一项为 visibility，第二项为 shading，它们两者的乘积 $visibility\cdot shading$ 正是 Shadow Mapping 的实现原理

此时想要它比较准确，那么根据上述情况就可以得出：

①Small support （积分域较小）时：取 V 为积分中单个结果，即点光源
②$g(x)$ 较为平滑时：此时 $L_i$ 为 constant radiance area lighting 或 $f_r$ 为 diffuse bsdf（因为 constant radiance area lighting 和 diffuse bsdf较为平滑）

Percentage closer soft shadows

这是一种做软阴影的方法：

在讲 PCSS 之前，先讲一下 PCF，因为 PCSS 是基于 PCF 的一种自适应做软阴影的方法

Percentage Closer Filtering (PCF)

PCF 是一种滤波方法，早期是用来做阴影边界的抗锯齿效果的，后面人们又发现可以通过它来滤波阴影比较的结果（Filtering the results of shadow comparisons），使得产生的阴影结果有过渡效果

需要注意的两点：

1. PCF 不是对最终的阴影结果的 filter

2. PCF 不是对 shadow mapping 第一趟得到的深度图（shadow map）的 filter
（这里的 filter 理解成平滑/平均就行了）

PCF 的做法：

1. 在 shadow mapping 的第二趟的比较深度的过程中，不是和一个像素进行比较，而是和一个窗口大小的像素进行比较

2. 对结果进行（加权）平均

这种方式也对应了前面所述的 $visibility\cdot shading$，由于此时 visibility 不是非0即1，所以得到的阴影也会出现逐渐消隐的效果

PCF 的结果：

PCSS 的原理

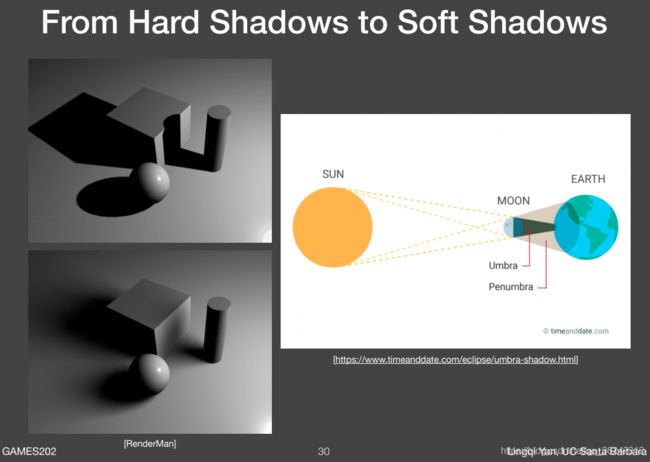
通过结果我们可以发现，PCF 滤波后的阴影会出现一定程度的过渡/渐隐，但是在实际中，我们看到的阴影的过渡/渐隐在不同位置的程度是不同的。换句话说，当阴影接收物离阴影投射物越近时，阴影越“硬”，反之阴影越“软”：

前面通过 PCF 我们可以做出软阴影，但是现在我们希望它在不同区域的阴影过渡/渐隐程度是不同的，所以这里就引入了 Percentage Closer Soft Shadows（PCF），来做这样一个自适应软阴影的效果

它的自适应是这样做的：

首先定义 blocker depth 用于描述面光源离阴影接收物的深度，receiver depth 描述面光源离阴影投射物的深度，$w_{Penumbra}$ 描述 PCF 的滤波窗口大小，$w_{Light}$ 描述面光源的面积

可以发现这里存在一个相似三角形：
$$w_{\text{Penumbra }}/w_{\text{Light }}=\left(d_{\text{Receiver }}-d_{\text{Blocker }}\right)/d_{\text{Blocker }}$$

当 blocker depth 离 receiver depth 越近时，得到的 $w_{\text{Penumbra }}$ 就越小，反之越大，这也符合真实世界的阴影 。所以通过引入 blocker depth ，我们就可以自适应的调整 PCF 的滤波窗口大小

一些其他问题：

①blocker depth 如何定义？

对于一个着色点来说， 在一定窗口范围内， shadow map 中能够挡住这个着色点的深度的平均值定义为 blocker depth

②面光源如何生成 shadow map？

面光源不可能生成 shadow map，为了模拟面光源生成的软阴影，通常是在面光源中选定一个位置（中点）先去模拟点光源

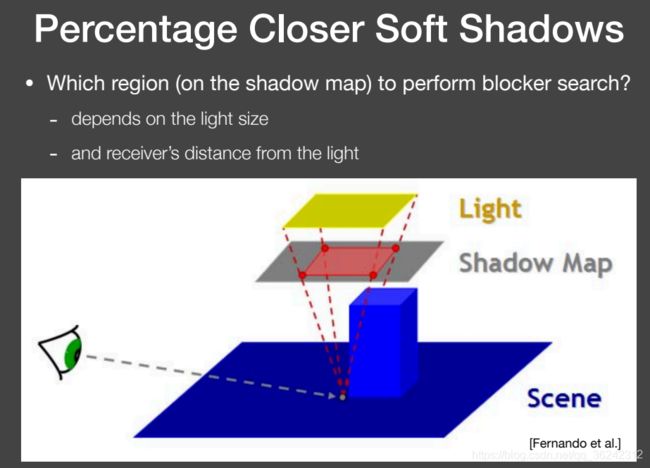
③生成 blocker depth 的搜索窗口范围如何规定？

取决于两点：

1. 面光源的大小
2. receiver 到光源的距离

PCSS 的结果：