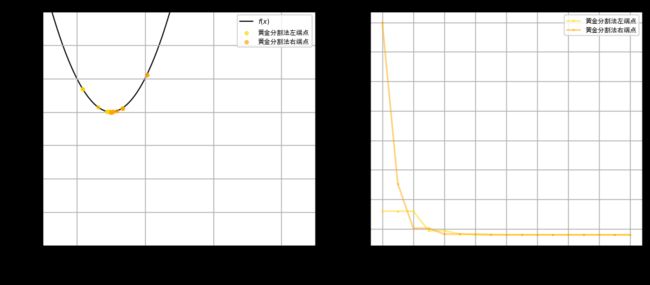
一维搜索的python实现
一维搜索python实现
求解函数的参数说明:
-
x1:初始迭代点,限牛顿法和梯度下降法
-
a,b:初始搜索区间的左右端点,限黄金分割法和对分法
-
iteration:最大迭代次数
-
delta:当迭代前后的x的差值的绝对值小于delta时,认为已经收敛,终止迭代
-
s:ax[0]的散点的大小,默认为3
-
alpha:ax[0]的散点的透明度,默认为0.5
求解一维搜索问题的过程:
-
在func函数中设置需要最优化的函数表达式
-
设置求解函数中的参数,除初始迭代点或初始迭代区间外均可取默认值
-
为使作图范围合适,在主函数中设置恰当的X和ax[0].set_xlim
-
运行主函数
导入必要包
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator #使x轴的坐标均为整数
import sympy as sp #符号求导用
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
定义需要优化的函数
def func(x):
if(isinstance(x, str) and x == 'sign'):
x = sp.symbols('x')
#y = pow(x, 4)+9*x*x-6*x+2 # 自定义要求解的函数
y=x*(x+2)
#y=pow(x,3)-2*t+1
return y
求导函数
def derivate(x1):
x = sp.symbols('x')
f = func('sign')
fx = sp.diff(f, x)
return float(fx.evalf(subs={x: x1}))
对分法
def Bisection(a,b,iteration=100, delta=1e-5,s=10,alpha=0.5): # a:左端点,b:右端点
dotx = [(a+b)/2] # 保存迭代点的横坐标,用来绘制折线图,先记录初始点
doty = [func((a+b)/2)] # 保存迭代点的纵坐标
n = 1 # 记录迭代次数
colors = "Lime"#绘图时使用的颜色
name = '对分法'#方法名,用于图例
l=a#需要迭代的左端点,初始为搜索区间的左端点
r=b#右端点
mid = (l+r)/2
for i in range(iteration):
dotx.append(mid) # 添加迭代点的横坐标
doty.append(func(mid)) # 添加迭代点的纵坐标
n = n+1
if(derivate(mid)<0):
l=mid
elif(derivate(mid)>0):
r=mid
else:
break;
if(abs(l-r)<delta):#左右端点距离足够小就结束迭代
break;
mid = (l+r)/2
ax[0].scatter(dotx, doty, marker='o', s=s, color=colors,
alpha=0.5, zorder=2, label=name) # 绘制迭代点
ax[1].plot(np.arange(0, n), doty, 'o-',
color=colors, markersize=1,label=name,alpha=0.5) # 绘制函数值下降曲线
#输出结果和迭代点
dotx = [round(x,3) for x in dotx] #迭代点保留3位小数
print(name+'的结果:'+'('+str(mid)+','+str(func(mid))+')')
print('中点的迭代点为:'+str(dotx))
return
牛顿法
def Newton(x, iteration=100, delta=1e-5,s=10,alpha=0.5): # 绘制迭代点和下降曲线
dotx = [x] # 保存迭代点的横坐标,用来绘制折线图,先记录初始点
doty = [func(x)] # 保存迭代点的纵坐标
n = 1 # 记录迭代次数
colors = "red"
name = '牛顿法'
for i in range(iteration):
if(derivate(x) < 1e-6):#防止导数为0
break
xnext = x-derivate(x)/(derivate(x+1e-6)-derivate(x-1e-6))*2e-6#把导数的数值微分作为二阶导数
dotx.append(xnext) # 添加迭代点的横坐标
doty.append(func(xnext)) # 添加迭代点的纵坐标
n = n+1
if(abs(x-xnext) < delta): # 终止条件
break
x = xnext
ax[0].scatter(dotx, doty, marker='o', s=s, color=colors,
alpha=0.5, zorder=2, label=name) # 绘制迭代点
ax[1].plot(np.arange(0, n), doty, 'o-',
color=colors, markersize=1,label=name,alpha=0.5) # 绘制函数值下降曲线
#输出结果和迭代点
dotx = [round(x,3) for x in dotx] #迭代点保留3位小数
print(name+'的结果:'+'('+str(x)+','+str(func(x))+')')
print('迭代点为:'+str(dotx))
return
梯度下降法
def Gradient(x, lr, iteration=100, delta=1e-5,s=10,alpha=0.5): # 绘制迭代点和下降曲线
dotx = [x] # 保存迭代点的横坐标,用来绘制折线图,先记录初始点
doty = [func(x)] # 保存迭代点的纵坐标
n = 1 # 记录迭代次数
colors = "navy"
name = '梯度下降法'
for i in range(iteration):
if(derivate(x) < 1e-6):#防止导数为0
break
xnext = x-derivate(x)*lr
dotx.append(xnext) # 添加迭代点的横坐标
doty.append(func(xnext)) # 添加迭代点的纵坐标
n = n+1
if(abs(x-xnext) < delta): # 新增的终止条件
break
x = xnext
ax[0].scatter(dotx, doty, marker='o', s=s, color=colors,
alpha=0.5, zorder=2, label=name) # 绘制迭代点
ax[1].plot(np.arange(0, n), doty, 'o-',
color=colors, markersize=1,label=name,alpha=0.5) # 绘制函数值下降曲线
#输出结果和迭代点
dotx = [round(x,3) for x in dotx] #迭代点保留3位小数
print(name+'的结果:'+'('+str(x)+','+str(func(x))+')')
print('迭代点为:'+str(dotx))
return
黄金分割法
def GoldDivide(a,b,iteration=100, delta=1e-5,s=10,alpha=0.5): # 绘制迭代点和下降曲线
dotx1 = [a] # 保存迭代点的横坐标,用来绘制折线图,先记录初始点
dotx2=[b]
doty1 = [func(a)] # 保存迭代点的纵坐标
doty2=[func(b)]
n = 1 # 记录迭代次数
colorsl = "gold"
colorsr = "orange"
name = '黄金分割法'
alpha=(np.sqrt(5)-1)/2
beta=1-(np.sqrt(5)-1)/2
t2=a+alpha*(b-a)
f2=func(t2)
t1=a+b-t2
f1=func(t1)
for i in range(iteration):
if(abs(t2-t1) < delta): #终止条件
t=(t1+t2)/2
break
if(f1<f2):
b=t2
t2=t1
f2=f1
t1=a+b-t2
f1=func(t1)
else:
a=t1
t1=t2
f1=f2
t2=a+b-t1
f2=func(t2)
dotx1.append(a) # 添加迭代点的横坐标
doty1.append(func(a)) # 添加迭代点的纵坐标
dotx2.append(b)
doty2.append(func(b))
n = n+1
t=(t1+t2)/2
ax[0].scatter(dotx1, doty1, marker='o', s=s, color=colorsl,
alpha=alpha, zorder=2, label=name+'左端点') # 绘制迭代点
ax[0].scatter(dotx2, doty2, marker='o', s=s, color=colorsr,
alpha=alpha, zorder=2, label=name+'右端点') # 绘制迭代点
ax[1].plot(np.arange(0, n), doty1, 'o-',color=colorsl, label=name+'左端点',markersize=1,alpha=0.5) # 绘制函数值下降曲线
ax[1].plot(np.arange(0, n), doty2, 'o-',color=colorsr, label=name+'右端点',markersize=1,alpha=0.5) # 绘制函数值下降曲线
#输出结果和迭代点
dotx1 = [round(x,3) for x in dotx1] #迭代点保留3位小数
dotx2 = [round(x,3) for x in dotx2] #迭代点保留3位小数
print(name+'的结果:'+'('+str(t)+','+str(func(t))+')')
print('左迭代点为:'+str(dotx1))
print('右迭代点为:'+str(dotx2))
return
主函数
# 画布的基础设置
X = np.linspace(-3, 5, 500) # X轴坐标数据
Y = func(X) # Y轴坐标数据
fig, ax = plt.subplots(1, 2, figsize=(10, 4), dpi=120) # 创建画布
ax[0].tick_params(labelsize=12) # 坐标字号
ax[1].tick_params(labelsize=12)
ax[1].xaxis.set_major_locator(MaxNLocator(integer=True))#函数的变化曲线的横坐标必须是整数
ax[0].set_xlabel('$x$') # 坐标名称
ax[0].set_ylabel('$y$')
ax[1].set_xlabel('迭代次数')
ax[1].set_ylabel('函数值')
ax[0].grid() # 增加网格
ax[1].grid()
ax[0].plot(X, Y, label="$f(x)$", color="black",
linewidth=1, zorder=1) # 作出函数图像
x0 = 2 #设置初始点,限牛顿法和梯度下降法
a=-3 #设置初始区间,限黄金分割法和对分法
b=5
#ax[0].scatter(x0, func(x0), color="black", s=10, label="初始点",zorder=3) # 绘制初始点,牛顿法和梯度下降用
# 函数求解与绘图
#Newton(x0, 100, delta=1e-1,s=10,alpha=0.8)
#print('\n')
#Gradient(x0, 0.02, 30, delta=1e-7,s=10,alpha=0.8)
#print('\n')
GoldDivide(a,b,iteration=100, delta=1e-3,s=10,alpha=0.8)
#print('\n')
#Bisection(a,b,iteration=100,delta=1e-1)
ax[0].set_xlim(-3,5)
ax[0].set_ylim(-5,2)
ax[0].legend(loc = 1, prop = {'size':6})#添加图例
ax[1].legend(loc = 1, prop = {'size':6})
plt.show()
黄金分割法的结果:(-1.0007739937854936,-0.99999940093362)
左迭代点为:[-3, -3, -3, -1.833, -1.833, -1.387, -1.111, -1.111, -1.111, -1.046, -1.046, -1.022, -1.006, -1.006, -1.006, -1.003, -1.003]
右迭代点为:[5, 1.944, 0.056, 0.056, -0.666, -0.666, -0.666, -0.836, -0.941, -0.941, -0.981, -0.981, -0.981, -0.991, -0.997, -0.997, -0.999]