2019独角兽企业重金招聘Python工程师标准>>> 
- 假设检验概念
参数估计是讨论用样本统计量估计总体参数的方法，总体参数μ在估计前是未知，而在假设检验中，则是先对μ的值做出一个假设，然后利用样本信息验证这个假设是否成立
- 检验统计量
- 一个总体参数的检验
- 统计量的确定
一、假设提出的问题
H0原假设，H1备择假设设定
1、原假设和备择假设互斥
2、先确定备择假设再确定原假设
3、等于号“=”总放在原假设上
4、因为研究目的的不同，对于同一问题的假设不一样，结论可能也不一样
5、原假设通常都是明确的
二、a显著水平
假设检验中的a，是指原假设正确时。人们却把它拒绝了的概率或者风险，它是公认小概率事件的概率值，必须在每一次统计检验之前确定，通常取
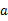=0.05或
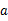=0.01，这表明，当做出接受原假设的决定时，其正确的可能性（概率）为95%或99%
=0.05或
=0.01，这表明，当做出接受原假设的决定时，其正确的可能性（概率）为95%或99%
显著性水平 - MBA智库百科
三、a与β错误
a错误：原假设是真的，但是我们却拒绝了
β错误：原假设是假的，但是我们却没有拒绝
一般首要控制a错误
β错误的影响因素
a、总体参数的真值：随着假设总体参数的减少而增大
b、显著水平a：当a减小时增大
c、总体标准差
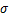：当
增大时增大
：当
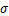增大时增大
d、样本容量n：n减小时增大
四、P值
1、在原假设为真的条件下，检验统计量的观察值大于或者等于其计算值的概率(通俗点说P值为当原假设为真时所得到的样本观察结果或更极端结果出现的概率)
P值很小，说明发生这种情况的概率很小，拒绝原价
理解
P值就是 原假设为真的概率，a 是显著性水平，代表小概率事件
当在双侧检验中 ， 当 a =0.05，P < 0.025（a/2=0.025） 则拒绝原假设（说明原假设出现的概率比小概率事件还要小，当然要拒绝），相反则接受原假设、
当在单侧检验中，当 a =0.05 ，P < 0.05 则拒绝原假设
--双侧检验为分布中两侧面积之和
2、反映实际观测到的数据一原假设H0之间不一致程度
3、被称为观察到的（或实测的）显著性水平
4、决策规则：（单侧检验）若p值
五、假设检验的结论表述
1、假设检验的目的在与试图找到拒绝原假设，而不是在证明什么是正确的
2、拒绝原假设时结论是清楚的，例如：H0：μ=10，拒绝H0，可以直接说μ=10
3、不拒绝原假设，并不能说明假设是正确，只能说当前没有充分数据，证明原假设是正确还是错误的
接受备择假设一定意味着原假设错误，没有拒绝原假设并不能说明备择假设一定错的