类EMD的“信号分解方法”及MATLAB实现（第七篇）——EWT

这是“类EMD”方法系列的第7篇，前几篇分别是EEMD、CEEMD、CEEMDAN、VMD、ICEEMDAN、LMD，想要看前几种方法的点击链接可以跳转。

经验小波变换（empirical wavelet transform,EWT）是2013年由Gilles提出[1]。这个方法是EMD方法和小波变换的结合，综合了EMD的自适应性和小波方法理论完备、计算简单快捷等特点。

1. EWT的概念

经验小波变换的核心思想其实并不难理解。

我们在做所谓的模态分解时，很多时候目的就是将不同频率段的信号单独提取出来，不过此时将面临一个难点：提取的频率范围该怎么选。之前提到的VMD方法是通过变分问题构造解决的这个问题；今天要介绍的EWT采用的是另外一个思路，即对信号的频谱进行分割划分，构建合适的小波滤波器组，对信号进行分解。

其分解过程大致如下：

步骤１：计算输入信号的傅里叶变换。
步骤２：将傅里叶频谱划分为Ｎ个连续段落，通过搜索频谱的局部极大值确定边界，并将其按降序进行排列，假设极大值个数为 Ｍ，当 Ｍ ≥Ｎ 时，保留前N－１个极大值，当 Ｍ＜Ｎ时，保留全部极大值并对Ｎ进行修正，最后，取两个局部极大值间的中间频率作为ωn。
步骤３：找到分割边界并分割频谱。
步骤4：构建合适的小波滤波器组，对信号进行分解。

相关的理论涉及比较繁复的计算过程，想要深入研究的同学可以看一下方法提出者的论文原文[1]，另外有一个PPT讲述了从EMD到EWT的推演过程[2]，有兴趣的话也可以看一下。

2.EWT的编程实现

ewt函数在MATLAB2020b版本中内置到官方库了，不过按照“类EMD”系列的代码的统一风格，笔者重新进行了封装，增加了绘制IMF分量与频谱对照的绘图函数,封装后的函数有两个。（另外，在MATLAB官方函数以外，还存在着第三方的ewt的工具箱，不过这里就不采用和集成了）

测试信号同样使用前两篇文章中的正弦信号与间断性高频脉冲合成的信号：

%% 1.生成仿真信号
fs = 400;  %采样频率
t = 0:1/fs:0.75; %时间轴
x = sin(2*pi*4*t); %低频正弦信号
y = 0.5*sin(2*pi*120*t); %高频正弦信号
for i = 1:length(t) %将高频信号处理成间断性
    if mod(t(i),0.25)>0.11&&mod(t(i),0.25)<0.12
    else
        y(i) = 0;
    end
end
sig = x+y; %信号叠加
figure('color','white')
plot(t,sig,'k') %绘制原始信号

（一）时域分解图

画EWT分解图的函数介绍如下：

function mra = pEWT(data,FsOrT)
% 画信号EWT分解图
% 输入：
% data为待分解信号
% FsOrT为采样频率或采样时间向量，如果为采样频率，该变量输入单个值；如果为时间向量，该变量为与y相同长度的一维向量。如果未知采样频率，可设置为1
% 输出：
% mra为经EWT分解后的各mra分量值
% 例1：（FsOrT为采样频率）
% fs = 100;
% t = 1/fs:1/fs:1;
% data = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% mra = pEWT(data,fs);
% 例2：（FsOrT为时间向量，需要注意此时FsOrT的长度要与y相同）
% t = 0:0.01:1;
% data = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% mra = pEWT(data,t);
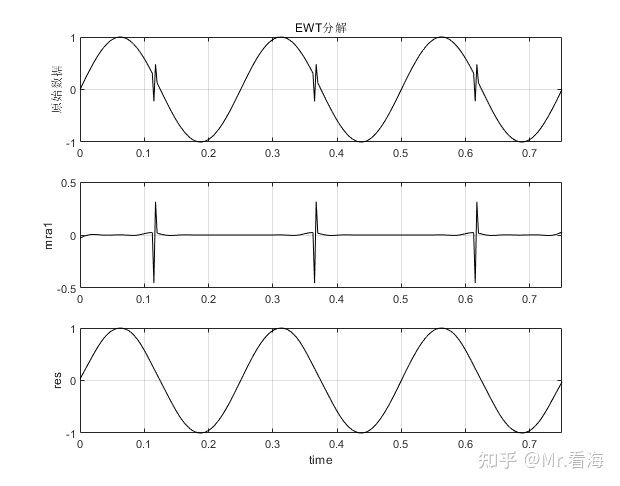
% 注意：该代码仅能在2020b及更新MATLAB版本中运行

应用上边的函数，画出的图是这样的：

注意，这里的分量没有用imf表示，而是用mra表示，即multiresolution analysis（多分辨率分析）

这个分解结果也可以说是完美的了，没有任何无效分量，有兴趣的同学可以翻一下之前EEMD、CEEMD、CEEMDAN、ICEEMDAN对同样一段信号做的分解效果，皆可以发现EWT的厉害之处了。

（二）时域分解图及对应频谱图

画EWT分解图及对应频谱图的函数介绍如下：

function mra = pEWTandFFT(y,FsOrT)
% 画信号EWT分解与各mra分量频谱对照图
% 输入：
% y为待分解信号
% FsOrT为采样频率或采样时间向量，如果为采样频率，该变量输入单个值；如果为时间向量，该变量为与y相同长度的一维向量
% 输出：
% mra为经EWT分解后的各mra分量值
% 例1：（FsOrT为采样频率）
% fs = 100;
% t = 1/fs:1/fs:1;
% y = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% mra = pEWTandFFT(y,fs);
% 例2：（FsOrT为时间向量，需要注意此时FsOrT的长度要与y相同）
% t = 0:0.01:1;
% y = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% mra = pEWTandFFT(y,t);

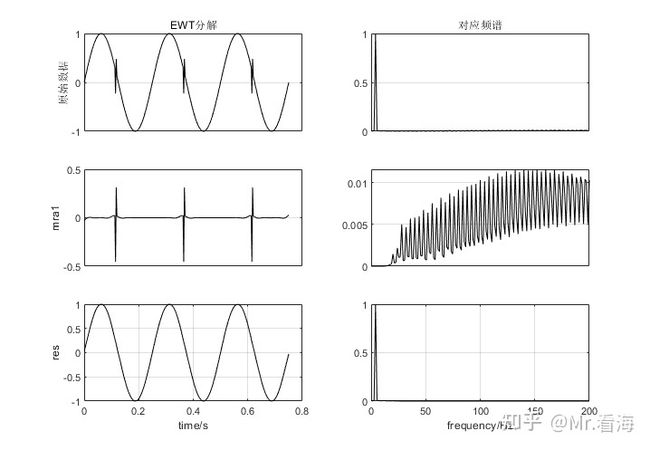
% 注意：该代码仅能在2020b及更新MATLAB版本中运行

画出的图是这样的：

上边的测试代码和封装函数，包括工具箱都可以在下述链接获取：

EWT画图工具（公开版） | 工具箱文档

EMD、EEMD、CEEMD、CEEMDAN、ICEEMDAN、VMD以及HHT相关的程序也有，编程不易，感谢支持~关于EMD、EEMD、CEEMD、VMD和HHT的相关介绍可以看这里：

Mr.看海：这篇文章能让你明白经验模态分解（EMD）——EMD在MATLAB中的实现方法

Mr.看海：希尔伯特谱、边际谱、包络谱、瞬时频率/幅值/相位——Hilbert分析衍生方法及MATLAB实现

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第一篇）——EEMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第二篇）——CEEMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第三篇）——CEEMDAN

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第四篇）——VMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第五篇）——ICEEMDAN

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第六篇）——LMD

参考

1. ^abGilles, Jérôme. “Empirical Wavelet Transform.” IEEE Transactions on Signal Processing 61, no. 16 (August 2013): 3999–4010. https://doi.org/10.1109/TSP.2013.2265222.
2. ^EWT讲解PPT http://pdfs.semanticscholar.org/3803/d42330506aff3a5cc5eaf69cf589c9c8929b.pdf