CEEMDAN：完全噪声辅助聚合经验模态分解（matlab）——学习笔记3

CEEMDAN：完全噪声辅助聚合经验模态分解——学习笔记3

从EMD到CEEMDAN

1.EMD

EMD算法将基于原始信号的局部特征时间尺度，将原始信号分解为特征模态函数，即将其分解为从高频到低频的一系列IMF分量。
算法分解步骤如下：

对于一个任意信号s(t)，通过三次样条插值分别提取出该信号的极大值、极小值包络线，根据得到的上下包络线计算得到均值曲线a(t)。则有：
$$h(t)=s(t)-a(t)$$
根据IMF分量成立条件判断h(t)是否为IMF分量，其中IMF作为单分量信号。其成立条件为：
（1）信号的局部极值点数和过零点数相等或至多相差一个，即信号中所有极大值和极小值围绕零轴线波动。
（2）在信号的任意一点上，由局部极大值和局部极小值分别连成的上包络线和下包络线的均值都为０。
如果h(t)满足条件，则有第一阶IMF分量：
$$IM{F}_1:c_1(t)=h(t)$$
第一阶剩余分量为：
$$r_1(t)=s(t)-c_1(t)$$
若r1(t)为非单调函数，则令：
$$s(t)=r_1(t)$$
再次通过三次样条插值取极值包络线，得到第2阶、第3阶……IMF分量，直到rn(t)为单调函数为止。
如果h(t)不满足条件，则令：
$$s(t)=h(t)$$
再次进行三次样条插值提取上下包络线，重复上述步骤，不断迭代，直到h(t)满足IMF分量条件为止。但是，为了让得到的分量具有物理意义，还需要对迭代次数进行限制，即仿柯西收敛准则，定义：
$$SD=\sum _{t=0}^T|h_{k-1}(t)-h_k(t){|}^2/h_{k-1}(t{)}^2$$
SD在0.2~0.3之间时，迭代筛选过程停止。

利用matlab自带的emd函数实现的emd分解如下：
采用一个任意的原始信号：

t=0.01:0.01:3;
f=10*sin(10*pi*t)+10*sin(20*pi*t)+20*sin(5*pi*t);
figure,plot(t,f,'linewidth',2.5),title('原始信号'),set(gcf,'color','w');

对其进行EMD分解，得到5个IMF分量：

[imf,residual]=emd(f,'Interpolation','spline','display',1);

EMD具有自适应性和多分辨率等特点，但是其缺点是：包络线拟合偏差，端点效应，模态混叠等。其中，模态混叠现象具体表现为：
（1）不同的特征频率出现在同一IMF分量中
（2）不同的IMF分量中存在相近的特征频率
针对模态混叠这一问题，又提出了其他三种分解方法：EEMD、CEEMD、CEEMDAN，它们都是建立在EMD算法的基础之上实现的。

---

2.EEMD&CEEMD

EEMD聚合经验模态分解与CEEMD互补聚合经验模态分解都是通过对原始信号添加足够多的随机白噪声，然后进行EMD分解，最后取平均值得到IMF分量。不同之处在于，CEEMD添加的噪声是成对的（一正一负），为的是解决EEMD中随机噪声残留的问题。这两种方法在此不做深究。

---

3.CEEMDAN

算法分解步骤如下：

其中$E_k(\ast )$为利用EMD算法产生的第k阶EMD分量，A(*)为计算的第一阶IMF分量所对应的一阶剩余分量，$\beta$为常数系数，w为添加的随机噪声。确定添加噪声的次数M，得到M个初始量$s_M(t)=s(t)+{\beta }_{k-1}{E}_k(w_M)$，对M个初始量采用EMD算法得到第一阶剩余分量，求平均值（/M）得到一阶平均剩余分量$r_1$，由公式：$c_1(t)=s(t)-r_1$可求出第一阶平均IMF分量，再令$s(t)=r_1$,重复上述步骤，以此类推，依次得到第2阶、第三阶IMF分量、……，直到$r_k$不能再被分解为止。

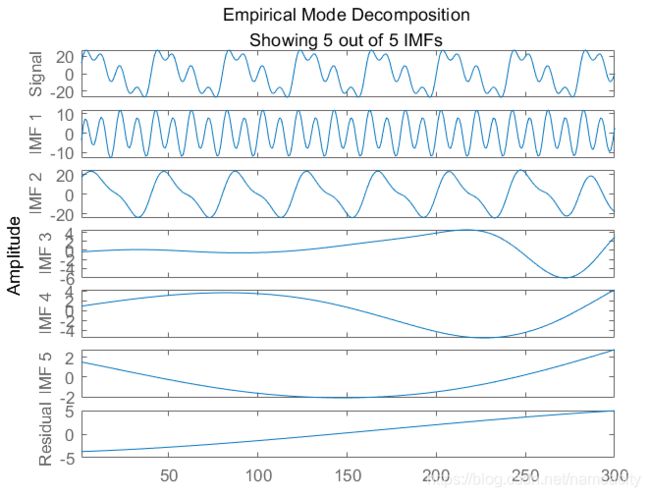
用matlab编写程序实现：
原始信号：

t=0.01:0.01:3;
f=10*sin(10*pi*t)+10*sin(20*pi*t)+20*sin(5*pi*t);
figure,plot(t,f,'linewidth',2.5),title('原始信号'),set(gcf,'color','w');

通过CEEMDAN算法得到的九个IMF分量：

[modes its]=ceemdan(f,0.2,500,5000);
t=1:length(f);

[a b]=size(modes);

figure;
subplot(a+1,1,1);
plot(t,f,'k');% the f signal is in the first row of the subplot
ylabel('f')
set(gca,'xtick',[])
axis tight;

color='rgbycmrgbycm';
for i=2:a
    subplot(a+1,1,i);
    plot(t,modes(i-1,:),color(i-1));
    ylabel (['IMF ' num2str(i-1)]);
    set(gca,'xtick',[])
    xlim([1 length(f)])
end

---

还可以对所分解得到的IMF分量进行选择，尤其是对于某些具有局部倾斜的信号，CEEMDAN算法可以很好的做到消除局部倾斜，选择的规则如下：
$$F=\sqrt{1/n\ast \sum _{i=1}^n[I_k(i)-I(i){]}^2}$$
i表示数据点数，n表示数据点总个数，$I_k(i)$表示第k阶IMF分量，$I(i)$表示原始信号，F最小值对应的就是应选择的分量信号。

对应的代码如下：

%找到需要的分解信号
[m,n]=size(modes);
scanstep=length(f);
f=0;
F=zeros(1,m);
for k=1:m
    for i=1:scanstep
        f=f+(modes(k,i)-f(1,i)).^2;
    end
     F(1,k)=sqrt((1/scanstep).*f);
end
minF_loc=find(F==min(min(F)))
figure,plot(t,modes(minF_loc,:)),xlabel('scanstep'),title(['第' num2str(minF_loc) '阶IMF分量(分解信号)']);

---

步骤流程图来自：

[1]陈净和. 基于噪声辅助经验模态分解的低温高速轴承故障诊断方法研究[D].北京交通大学,2019.

---

具体的程序参考：
https://download.csdn.net/download/nameacity/21390286