水平集图像分割并行加速算法设计与实现(串行、OpenMP、CUDA)——原理篇

本次水平集图像分割并行加速算法设计与实现包含：原理篇、串行实现篇、OpenMP并行实现篇与CUDA GPU并行实现篇四个部分。
原理篇主要讲解水平集图像分割的原理与背景。串行实现篇、OpenMP并行实现篇与CUDA GPU并行实现篇主要基于C++与OpenCV实现相应的图像分割与并行加速任务。本系列属于图像处理与并行程序设计结合类文章，希望对你有帮助。

背景

图像分割是一经典难题，发展至今仍没有一种囊括全部图像的通用分割技术，同时图像分割结果好坏也没有统一的标准。通常人们只对图像中的某一部分感兴趣，图像中的这一部分具有特殊性质，可以是单一区域，也可以是多个区域，称之为目标（前景），其余部分则被称为背景。在实际应用中，为了完成目标识别或特定任务，需要提取出图像中的目标，这是图像分割研究的重点。

基于主动轮廓模型的水平集图像分割技术以独特的优势在图像分割领域受到广泛关注。其优点主要体现于:

1. 该方法与图像的特征信息充分结合，使得曲线的演化具备良好的拓扑性质；
2. 将图像的离散性转化为具有连续性的泛函；
3. 由于数学理论具备完备性，可很好地把图像分割理论与数学物理方程结合。

基于上述优势，在图像分割技术中，水平集模型得到了广泛的应用，具有良好的发展前景和发展潜力。

理论基础

主动轮廓模型

基本思想

通过在图像中演化一组动态曲线，自适应地控制曲线的演化速度，使得其停驻在物体边缘处，从而检测出图像中感兴趣的物体。具体主动轮廓模型演化过程示例如下所示：

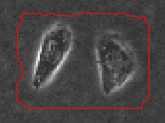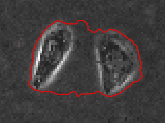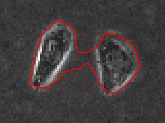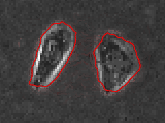
分类

1. 参数化主动轮廓：Snake(存在对初始位置敏感，可能收敛到局部极值点等问题)
2. 几何主动轮廓：水平集方法 (level set)

CV水平集模型

本次并行图像处理算法设计基于CV水平集模型，其是由Chan和Vese在Mumford D等研究人员提出的(MS)模型基础上构建的。论文原文具体链接如下：
CVPR原文链接
下面将对CV水平集模型原理进行详细介绍。

能量函数

假定待分割的图片为$u_0$，其仅仅由两个区域构成，图中的任何一个点用$u_0(x,y)$进行表示。现需要获得被曲线C包围的前景轮廓，让曲线C经过演化恰好停留在待分割物体的边缘处，由此提出式(1)中的能量函数。

$$\begin{array}{c}F(C)={\int }_{\text{isside }(C)}{\left|u_0(x,y)-c_1\right|}^{2}dxdy+{\int }_{\text{outside }(C)}{\left|u_0(x,y)-c_2\right|}^{2}dxdy\end{array}\text{\hspace{1em}(1)}$$
(1)式中的常数$c_1$和$c_2$分别是曲线C内部像素点的均值和C外部像素点的均值。设定原图$u_0$被曲线C分割为前景-inside(C)和背景-outside(C)两部分。对于待分割的图片$u_0$来说，当上述能量函数值最小时，所得的曲线C就是我们希望得到的待分割物体的轮廓（分割出的前景值更接近实际目标均值，分割出的背景值更接近实际背景均值）。为了更好的对图像进行分割，同时实现(1)式中能量函数的最小化，为其添加长度项与面积项作为正则项，由此将能量函数重新定义为式(2)所示。
$$\begin{array}{c}\begin{array}{rl}F(C)=\mu & \mathrm{Length}(C)+v\cdot \mathrm{Area}(\text{ inside }(C))\\ & +{\lambda }_1{\int }_{\text{inside }(C)}{\left|u_0(x,y)-c_1\right|}^{2}dxdy\\ & +{\lambda }_2{\int }_{\text{outside }(C)}{\left|u_0(x,y)-c_2\right|}^{2}dxdy\end{array}\end{array}\text{\hspace{1em}(2)}$$
其中$\mu ⩾0,v⩾0,{\lambda }_1,{\lambda }_2>0$。
为演化与求解(2)式中能量函数的最小值，可将曲线从二维升维到三维进行演化处理，即把关于曲线C的能量函数改写为关于水平集函数ϕ的能量函数，其后通过零水平集的演化模拟曲线的演化，以此实现相应的图像分割。具体升维操作，以及三维演化与二维演化对应关系如下图所示。（其中蓝色平面为z=0平面，灰色轮廓为零水平集对应轮廓）

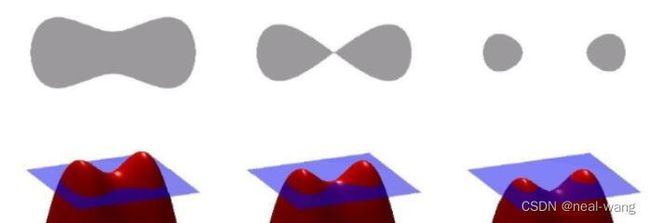
在运用水平集对曲线进行替换之前需要引入两个函数：Heaviside函数与Dirac函数。Heaviside函数本质为一阶跃函数，用于对零水平集的内外进行划分，具体如式(3)所示。
$$\begin{array}{c}H(z)=\{\begin{array}{ll}1& z\ge 0\\ 0& z<0\end{array}\end{array}\text{\hspace{1em}(3)}$$
Dirac函数本质为一冲激函数，主要用于在长度项中提取水平集轮廓线，具体如式(4)所示。
$$\begin{array}{c}\delta (z)=\frac{d}{dz}H(z)\end{array}\text{\hspace{1em}(4)}$$
由此可将能量函数转化为(5)式所示。
$$\begin{array}{c}\begin{array}{rl}& F\left(c_1,c_2,\varphi \right)=\mu {\int }_{\Omega }\delta (\varphi (x,y))|\nabla \varphi (x,y)|dxdy+v{\int }_{\Omega }H(\varphi (x,y))dxdy\\ & +{\lambda }_1{\int }_{\Omega }{\left|u_0(x,y)-c_1\right|}^{2}H(\varphi (x,y))dxdy\\ & +{\lambda }_2{\int }_{\Omega }{\left|u_0(x,y)-c_2\right|}^2(1-H(\varphi (x,y)))dxdy\end{array}\end{array}\text{\hspace{1em}(5)}$$
其中的$c_1$和$c_2$可以通过水平集函数ϕ求出，具体如式(6)所示。
$$\begin{array}{c}\{\begin{array}{l}{c}_1(\varphi )=\mathrm{average}\left(u_0\right)\text{ in }\{\varphi \ge 0\}\\ c_2(\varphi )=\mathrm{average}\left(u_0\right)\text{ in }\{\varphi <0\}\end{array}\end{array}\text{\hspace{1em}(6)}$$

变分法泛函求极值

针对泛函极值问题，可以运用变分法进行求解。根据欧拉-拉格朗日方程，可得其能量函数的梯度，并基于最陡梯度下降算法，进一步推导出水平集函数ϕ演化方程为式(7)所示。
$$\begin{array}{c}\frac{\partial \varphi }{\partial t}={\delta }_{ϵ}(\varphi )\left[\mu \cdot \mathrm{div}\left(\frac{\nabla \varphi }{|\nabla \varphi |}\right)-v-{\lambda }_1{\left(u_0-c_1\right)}^2+{\lambda }_2{\left(u_0-c_2\right)}^2\right]\end{array}\text{\hspace{1em}(7)}$$
由于冲击函数Dirac几乎处处为0，由此添加ϵ项对其进行平滑处理。由此改变Heaviside函数与Dirac函数为式(8)与(9)形式。
$$\begin{array}{c}{H}_{ϵ}=\frac{1}{2}\left(1+\frac{2}{\pi }\arctan \left(\frac{z}{ϵ}\right)\right)\end{array}\text{\hspace{1em}(8)}$$

$$\begin{array}{c}{\delta }_{ϵ}=H_{ϵ}^{\prime }=\frac{ϵ}{\pi }\frac{1}{z^2+{ϵ}^2}\end{array}\text{\hspace{1em}(9)}$$

当ϵ→0时，式(8)与式(9)分别收敛于式(3)与式(4)，且此时δϵ的支撑集是整个实数集R，不管初始曲线是何种形态，都可以得到全局最优解。

迭代演化求解

在实际实现过程中运用差分代替偏微分进行演化求解，其具体演化方程为式(10)所示。
$$\begin{array}{c}\begin{array}{rl}\frac{{\varphi }_{i,j}^{n+1}-{\varphi }_{i,j}^n}{\Delta t}& =L\left({\varphi }_{i,j}^n\right)\\ & ={\delta }_h\left({\varphi }_{i,j}^n\right)\left[\mu \left({\text{ curvature }}_{ij}\right)-v-{\lambda }_1{\left(u_{0,i,j}-c_1\right)}^2+{\lambda }_2{\left(u_{0,i,j}-c_2\right)}^2\right]\end{array}\end{array}\text{\hspace{1em}(10)}$$
(10)式中的差分方程可以转化为如下所示迭代形式：
$$\begin{array}{c}{\varphi }_{i,j}^{n+1}=L\left({\varphi }_{i,j}^n\right)\Delta t+{\varphi }_{i,j}^n\end{array}\text{\hspace{1em}(11)}$$
由此可通过循环迭代，完成水平集图像分割的演化求解。
下期将基于上述原理对水平集图像分割串行算法进行设计与实现，欢迎关注！