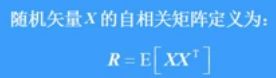计算机视觉与模式识别概念

模式：相同或相似的事物,要被识别的对象的数字化

模式类：相同或相似事物的全体（概率里的总体）

模式样本：对具体事物观测的观测数据

模式分布：大量观测获取的分布

模式识别：用计算机实现人类对环境中的事物进行识别，模式识别可以划分为“分类”和“回归”两种形式。本质是一种推理（inference过程）

模式识别的数学解释：模式识别可以看做一种函数映射f（x），将待识别模式x从输入空间映射到输出空间。函数（x）是关于已有知识的表达。

 

 

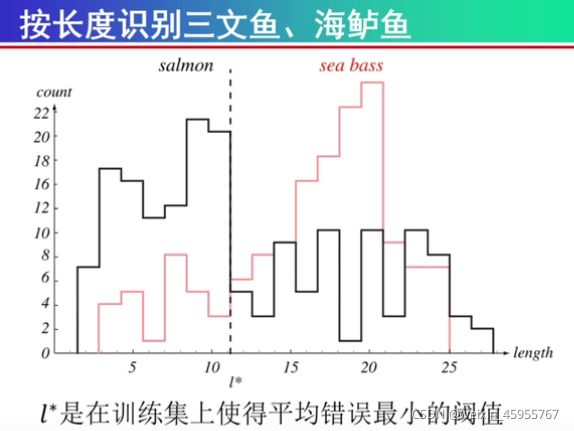
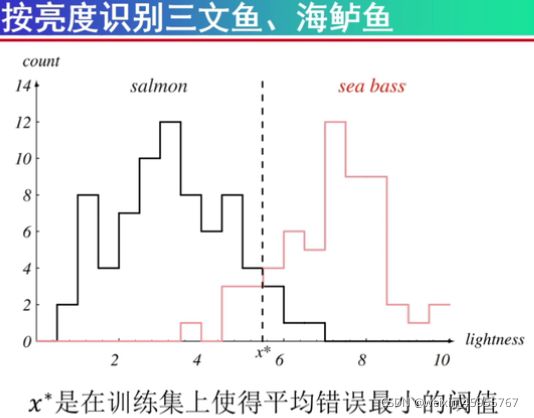
可以看出亮度分类效果比较好

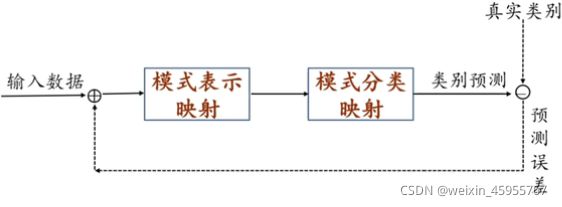
模式表示：从观察空间到表示空间的映射（就是特征提取），包括特征矢量，符号串，图，关系式

模式分类：从表示空间到类别空间的映射（分类器设计）

 

 输入数据就是训练样本

每个训练样本 , 都是通过采样得到的一个模式，即输入特征空

间中的一个向量；通常是高维度（即 p 很大），例如一幅图像。

训练样本可以认为是尚未加工的原始知识，模型则是经过学习（即加工

整理归纳等）后的真正知识表达。

所有训练样本假设满足independent and identical distribution (iid) 。

如果想学得好，这组训练样本要覆盖模型所有可能的分布空间。

模型：

        1.学习的是模型的参数

        2.模型的结构式设计人员事先给定的

        3.学习模型结构是当前和未来机器学习领域的研究内容之一

        线性模型

                1.模型本身就是直线，平面，超平面

                2.什么用？ 用来分线性可分的数据

        非线性模型

                1.模型本身是曲线，曲面，超曲面

                2.什么用？适用于线性不可分/线性不可表达的数据

                3.多项式，决策树都是非线性模型（多项式竟然是非线性模型）

 模型参数量和样本数量的关系

                为什么可以表达为线性方程的解？

                        已知方程的结构和解然后求方程的系数

                        训练样本就是方程的解

               模型参数量和样本数量的关系

                        训练样本数 等于  超参数个数  超参数有唯一解（几个方程，几个未知量的问题

或者就是AX=y 其中特征矩阵和参数矩阵满秩）

                        训练样本数 >  超参数个数   超参数有多个解

                        训练样本数<超参数个数     超参数没有解

 目标函数：也叫损失函数（损失是目标函数实现的方式之一）

        什么地方用：训练模型的时候用

        有什么用： 给参数解加入约束条件

优化算法和目标函数的关系：

        优化算法是最小化或最大化目标函数获取对应模型参数的方法

        很常见的例子：SGD,Adam

机器学习的方式：

        真值？ 是训练集的标签

        监督学习，无监督学习，半监督学习，强化学习

模型性能的评估方法：

        留出法竟然是评估方法而不是训练方法

        k折交叉验证

模型性能的评估指标：

        

        精度（Precision）：预测为阳性样本的准确程度。在信息检索领域，也

称作查准率。

        召回率（Recall）：也称作敏感度（sensitivity），全部阳性样本中被预

测为阳性的比例。在信息检索领域也称作查全率。

        

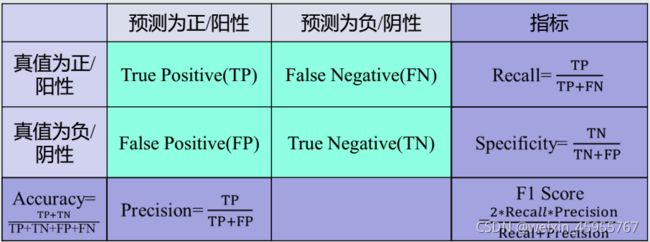
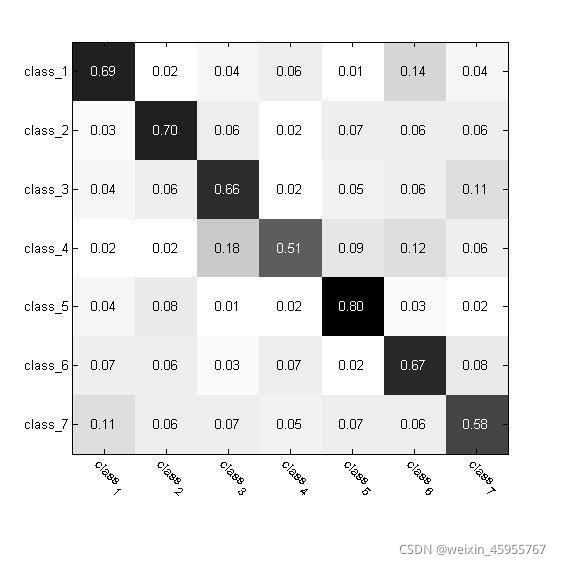
         混淆矩阵：

                

                    每一列加起来都是1，代表预测值

                    每一行代表标签

                    显然对角线越大越好

模式识别的经典问题：

        相似性度量：两个点的相似度

                欧式距离：

                        

         特征选择：选择哪些特征，选对分类的贡献最大的特征

        维数灾难：太多的特征引起的计算量

        信息融合（特征融合，融合决策）

        过拟合：训练集上过拟合，a榜过拟合

        统计模式识别：利用分布特征，隐含的概率密度函数进行分类

        结构模式识别：将对象分为诺干个基本单元，通过对句子进行句法分析，根据文法决定类别

        人工神经网络方法：用神经网络连接的非线性动态方法 来分类

        模糊模式识别

 模式识别基本原则：

1.没有免费的午餐：复杂的模型就有大的训练量

2.丑小鸭定理：只有不好的特征，没有不好识别的类

3.最小描述原理：算法要和语言解耦

预处理

        去噪声：消除或减少模式采集中的噪声及其其他干扰

        去模糊：消除或减少数据图像模糊

        模式结构转换：把非线性模式转变为线性模式

        预处理方法：滤波，变换，编码，归一化

贝叶斯决策理论：

        最小错误概率：各个模式分类错误的概率的加权和

特征：用于区分不同模式，可以测量的量

1.特征矢量：对象特征量测值组成的矢量，代表对象的模式，对对象的特征识别就是对特征矢量进行分类识别

2.特征空间：特征矢量的总体就是特征空间 特征矢量x就是特征空间的一个点

                  每个坐标轴代表一维特征

                 空间中的每个点代表一个模式（样本）

                 从坐标原点到任意一点（模式）之间的向量即为该模式的特征向量

3.随机变量：按照统计规律随机分布，概率不为1的特征测量值

4.随机矢量的分布函数：随机矢量X的联合分布概率分布函数F（x）=P(X<=x)  X是矢量

5.联合概率密度函数：代表单位区域的概率

 6.随机矢量的数字特征

       均值矢量：随机矢量的均值

       

        条件期望：模式识别中以类别为条件计算均值矢量叫做条件期望

        

     7.随机矢量的描述

        n维随机矢量用协方差矩阵表示

 

      自相关矩阵

      

    自相关矩阵和协方差阵区别

      

       相关系数

        

         协方差矩阵的非负定性：

        

 8.随机变量和随机矢量间的统计关系

        不相关：特征矢量的两个分量相乘取期望等于两个分量分别取期望相乘

        

         

          正交：两个矢量相乘的期望=0就是正交

        

         独立：独立必不相关

         两个随机矢量联合概率密度函数=两个随机矢量的概率密度函数相乘。就称X和Y独立

     9.随机矢量的变换

               设随机矢量Y是另一随机矢量X的连续函数