04 第三章 命题逻辑的推理理论
离散数学与组合数学汇总
文章目录
- 3.1 推理的形式结构
-
- 推理的形式结构
- 推理定律-重言蕴涵式
- 3.2 自然推理系统P
-
- 形式系统
- 自然推理系统
- 在自然推理系统P中构造证明
-
- 直接证明法
- 附加前提法
- 归谬法(反证法)
主要内容
推理的形式结构
- 推理的正确与错误
- 推理的形式结构
- 判断推理正确的方法
- 推理定律
自然推理系统P
- 形式系统的定义与分类
- 自然推理系统P
- 在P中构造证明:直接证明法、附加前提证明法、归谬法
3.1 推理的形式结构
推理的形式结构
定义3.1 设A1, A2, …, Ak, B为命题公式. 若对于每组赋值,
A1∧A2∧…∧Ak 为假,或当A1∧A2∧…∧Ak为真时,B也为真,
则称由前提A1, A2, …, Ak推出结论B的推理是有效的或正确
的 , 并称B是 有效结论 .
定理3.1 由命题公式A1, A2, …, Ak 推B的推理正确当且仅当
A1∧A2∧…∧Ak→B为重言式
注意: 推理正确不能保证结论一定正确
判断推理是否正确的方法:
- 真值表法
- 等值演算法
- 主析取范式法
推理定律-重言蕴涵式
1. A ⇒ (A∨B) 附加律
2. (A∧B) ⇒ A 化简律
3. (A→B)∧A ⇒ B 假言推理
4. (A→B)∧¬B ⇒ ¬A 拒取式
5. (A∨B)∧¬B ⇒ A 析取三段论
6. (A→B)∧(B→C) ⇒ (A→C) 假言三段论
7. (A↔B)∧(B↔C) ⇒ (A↔C) 等价三段论
8. (A→B)∧(C→D)∧(A∨C) ⇒ (B∨D) 构造性二难
(A→B)∧(¬A→B) ⇒ B 构造性二难(特殊形式)
9. (A→B)∧(C→D)∧(¬B∨¬D) ⇒ (¬A∨¬C) 破坏性二难
每个等值式可产生两个推理定律。如,由 A ⇔ ¬¬A可产生 A ⇒ ¬¬A和 ¬¬A ⇒ A
3.2 自然推理系统P
形式系统
定义3.2 一个形式系统 I 由下面四个部分组成:
(1) 非空的字母表,记作 A(I).
(2) A(I) 中符号构造的合式公式集,记作 E(I).
(3) E(I) 中一些特殊的公式组成的公理集,记作 AX(I).
(4) 推理规则集,记作 R(I).
记I=
形式语言系统,
自然推理系统: 无公理, 即AX(I)=Ø
公理推理系统 推出的结论是系统中的重言式, 称作定理
自然推理系统
定义3.3 自然推理系统 P 定义如下:
- 字母表
(1) 命题变项符号:p, q, r, …, pi, qi, ri, …
(2) 联结词符号:¬, ∧, ∨, →, ↔
(3) 括号与逗号:(, ), , - 合式公式(同定义1.6)
- 推理规则
(1) 前提引入规则
(2) 结论引入规则
(3) 置换规则
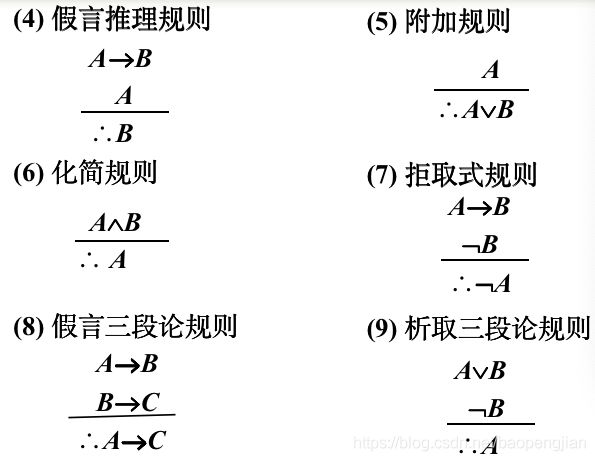

在自然推理系统P中构造证明
设前提A1, A2,…, Ak,结论B及公式序列C1, C2,…, Cl. 如果每
一个Ci(1 <= i<=l)是某个Aj, 或者可由序列中前面的公式应用推理
规则得到, 并且Cl =B, 则称这个公式序列是由A1, A2,…, Ak推
出B的证明
直接证明法
(1) 设命题并符号化
(2) 写出证明的形式结构
(3) 证明
例2 构造下面推理的证明:
若明天是星期一或星期三,我明天就有课. 若我明天有
课,今天必备课. 我今天没备课. 所以,明天不是星期一、
也不是星期三.
解 (1) 设命题并符号化
设 p:明天是星期一,q:明天是星期三,
r:我明天有课,s:我今天备课
(2) 写出证明的形式结构
前提:(p∨q)→r, r→s, ¬s
结论:¬p∧¬q
(3) 证明
① r→s 前提引入
② ¬s 前提引入
③ ¬r ①②拒取式
④ (p∨q)→r 前提引入
⑤ ¬(p∨q) ③④拒取式
⑥ ¬p∧¬q ⑤置换
附加前提法
用于结论为蕴涵式
欲证
前提:A1, A2, …, Ak
结论:C→B
等价地证明
前提:A1, A2, …, Ak, C
结论:B
归谬法(反证法)
欲证
前提:A1, A2, … , Ak
结论:B
做法
在前提中加入¬B,推出矛盾.
理由
A1∧A2∧…∧Ak→B
<=> ¬(A1∧A2∧…∧Ak)∨B
<=> ¬(A1∧A2∧…∧Ak)vB
<=>¬(A1∧A2∧…∧Ak∧¬B)∨0
<=> A1∧A2∧…∧Ak∧¬B→0
