LeetCode 590. N-ary Tree Postorder Traversal

Given the root of an n-ary tree, return the postorder traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [5,6,3,2,4,1]

Example 2:

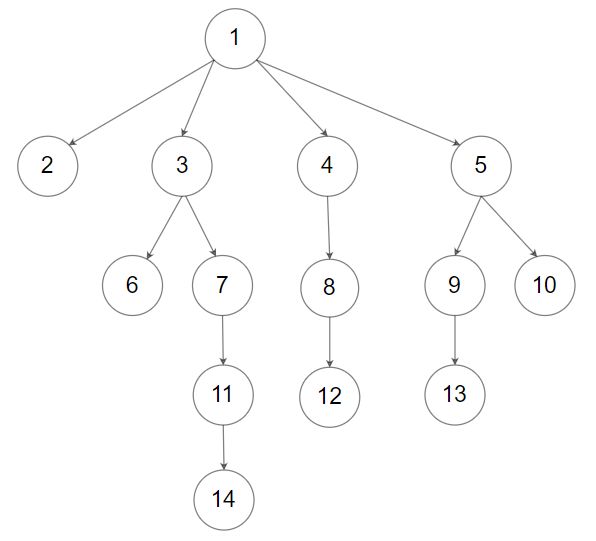
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [2,6,14,11,7,3,12,8,4,13,9,10,5,1]

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• 0 <= Node.val <= 104
• The height of the n-ary tree is less than or equal to 1000.

Follow up: Recursive solution is trivial, could you do it iteratively?

---

递归，也是很简单，只是变成了先遍历children再加root.val。

/*
// Definition for a Node.
class Node {
    public int val;
    public List children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List postorder(Node root) {
        List result = new ArrayList<>();
        helper(root, result);
        return result;
    }
    
    public void helper(Node root, List result) {
        if (root == null) {
            return;
        }
        for (Node node : root.children) {
            helper(node, result);
        }
        result.add(root.val);
    }
}

---

迭代，还是记着Stack + Set的方法呢，但是，debug了巨久都没搞出来，大概是seen set的地方弄错了。想着应该要把所有children都seen了才能pop它，但是刚开始想的是seen表示这个node有没有见过，于是要check所有children都seen了还挺麻烦，也不太确定这个思路对不对，就去看了答案。居然几乎没什么人跟我一个思路，看了一个相似的代码，才确认了确实是只有当node没有chidlren或者children全都seen过了才能pop，于是就把seen的含义变成了这个node的所有children是不是都seen过，调整了seen.add的位置，代码就很简洁也一下就没bug了。也算是加深了对postorder iterative的理解。

/*
// Definition for a Node.
class Node {
    public int val;
    public List children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List postorder(Node root) {
        List result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        Deque stack = new ArrayDeque<>();
        Set seen = new HashSet<>();  // this node's children are all seen
        stack.push(root);
        while (!stack.isEmpty()) {
            Node node = stack.peek();
            int size = node.children.size();
            if (size == 0 || seen.contains(node)) {
                node = stack.pop();
                result.add(node.val);
            } else {
                for (int i = size - 1; i >= 0; i--) {
                    Node child = node.children.get(i);
                    if (!seen.contains(child)) {
                        stack.push(child);
                    }
                }
                seen.add(node);
            }
        }
        return result;
    }
}