OpenBLAS学习一:源码架构解析&GEMM分析
- 1. 什么是OpenBLAS
- 1.1. BLAS
- 1.2. 功能
- 1.3. 使用
- 1.3.1. 编译
- 1.3.2. 调用
- 1.3.3. 定制化 build
- 2. OpenBLAS实现
- 2.1.
TOP_DIR - 2.2. 软件层次
- 2.3. Interface层
- 2.4. driver层
- 2.5. kernel层
- 2.1.
- 3. 总结
- 4. 附录1 reference
1. 什么是OpenBLAS
1.1. BLAS
BLAS (basic linear algebra subprogram) 是线性数学的基本计算,包括标量,矢量,矩阵之间的计算,分别称为Level1~3的操作。
由于level3的操作复杂度较高,于是产生了针对不同平台做优化的BLAS实现,包括 AMD Core Math Library (ACML), Arm Performance Libraries, ATLAS, Intel Math Kernel Library (MKL), 及我们要介绍的 OpenBLAS。
另外还要介绍一下 LAPACK,LAPACK是high-level的线性计算库,比如求解特征值,奇异值分解等。也是 OpenBLAS 支持的功能。
OpenBLAS
OpenBLAS 简单说就是 BLAS+LAPACK 在多种CPU上的重新实现。使用 C,Fortran 语言。OpenBLAS不支持GPU。
OpenBLAS 是gotoBLAS的一个分支,gotoBLAS在2008年开始停止更新。
这篇文章仅关注 BLAS 的实现,LAPACK 不在本文的考虑范围内,OpenBLAS 支持 Fortran 和 C 两个版本,我们关注C版本,对应头文件为 cblas.h。
下面提到的 OpenBLAS 都是指其中的 CBLAS 部分。
1.2. 功能
包括level 1, 2, 3,分别指矢量和矢量,矢量和矩阵,矩阵和矩阵间的计算,对应的复杂度分别是 O ( n ) , O ( n 2 ) , O ( n 3 ) O(n), O(n^2), O(n^3) O(n),O(n2),O(n3)。很多科学计算,以及当下热门的深度学习的核心运算 CONV, FC 等都可以转化成矩阵乘法。
自然 level3 的性能是大家关注的重点。
1.3. 使用
1.3.1. 编译
包括 make, cmake 两套编译系统,都可以编译。
make直接在 TOP_DIR 下 make 即可,cmake 编译则按如下方式执行
cd cmake
cmake .. # 生成相应的源码和makefile
cmake --build .. # 编译生成库,生成的库文件在 `lib/` 下
OpenBLAS 默认会读取 CPU 配置,其型号(如 x86_64,HASWELL) core_num 会被读取作为默认配置。我的设备直接 make 的编译结果如下,库文件在 TOP_DIR 下。
OpenBLAS build complete. (BLAS CBLAS LAPACK LAPACKE)
OS ... Linux
Architecture ... x86_64
BINARY ... 64bit
C compiler ... GCC (cmd & version : cc (Ubuntu 7.5.0-3ubuntu1~18.04) 7.5.0)
Library Name ... libopenblas_haswellp-r0.3.13.dev.a (Multi-threading; Max num-threads is 16)
To install the library, you can run "make PREFIX=/path/to/your/installation install".
libopenblas_haswellp-r0.3.13.dev.a 表示多线程并行版本。
1.3.2. 调用
CBLAS调用方式如下。
以 gemm (generic matrix multiply)为例,实现的功能为
C = α A ∗ B + β C C = \alpha A * B + \beta C C=αA∗B+βC
A , B , C A, B, C A,B,C都是矩阵,维度分别是 M × K , K × N , M × N M\times K, K\times N, M\times N M×K,K×N,M×N
接口如下,其中 order 表示数据排布方式,包括 row-major,col-major 两种方式,分别表示以行/列方向连续排布数据。lda 即矩阵A 的 leading dimension,以 row-major 为例,lda = K。
#include "cblas.h"
int main()
{
double A[6] = {1.0,2.0,1.0,-3.0,4.0,-1.0};
double B[6] = {1.0,2.0,1.0,-3.0,4.0,-1.0};
double C[9] = {.5,.5,.5,.5,.5,.5,.5,.5,.5};
// dgemm C 版本接口
/* void cblas_dgemm(OPENBLAS_CONST enum CBLAS_ORDER Order,
OPENBLAS_CONST enum CBLAS_TRANSPOSE TransA,
OPENBLAS_CONST enum CBLAS_TRANSPOSE TransB,
OPENBLAS_CONST blasint M,
OPENBLAS_CONST blasint N,
OPENBLAS_CONST blasint K,
OPENBLAS_CONST double alpha,
OPENBLAS_CONST double *A,
OPENBLAS_CONST blasint lda,
OPENBLAS_CONST double *B,
OPENBLAS_CONST blasint ldb,
OPENBLAS_CONST double beta,
double *C,
OPENBLAS_CONST blasint ldc);*/
cblas_dgemm(CblasColMajor, CblasNoTrans, CblasNoTrans,3,3,2,1,A, 3, B, 3,2,C,3);
for(int i=0; i<9; i++)
printf("%lf ", C[i]);
printf("\n");
}
1.3.3. 定制化 build
单线程版本
修改Makefile.system,在其中添加 NUM_THREADS=1,再make,生成库文件。
仅编译 BLAS
可以运行 make blas 仅生成 BLAS 库,不生成 LAPACK 。或者在 Makefile 中添加 NO_FORTRAN=1 NO_LAPACK=1 即可。
也可以 ONLY_CBLAS 只配置该参数。但是实际修改后,编译benchmark 或者编译 utest 都出现找不到 dgemm_ 的定义的问题。
支持多平台
一个库想要支持多个平台,DYNAMIC_ARCH 配置为1。
2. OpenBLAS实现
OpenBLAS 的目的是为了广泛支持主流 CPU, OS,并且提供不俗的性能。下面我们分析一下 OpenBLAS 是如何做到这两点的。
2.1. TOP_DIR
工程目录如下,实际上在 TOP_DIR 层还有很多文件,不是很友好。BLAS 相关的源码在 driver, interface, kernel 三个目录下。
OpenBLAS/
├── benchmark Benchmark codes for BLAS
├── cmake CMakefiles
├── ctest Test codes for CBLAS interfaces
├── driver Implemented in C
│ ├── level2
│ ├── level3
│ └── others Memory management, threading, etc
├── exports Generate shared library
├── interface Implement BLAS and CBLAS interfaces (callinkernel)
│ ├── lapack
│ └── netlib
├── kernel Optimized assembly kernels for CPU architectures
│ ├── arm64
│ ├── generic General kernel codes written in plain C.
│ ├── mips
│ ├── x86_64
│ └── ...
├── lapack Optimized LAPACK codes (replacing those iPACK)
│ ├── getf2
│ └── ...
├── lapack-netlib LAPACK codes from netlib reference implementation
├── reference BLAS Fortran reference implementation (unused)
├── relapack Elmar Peise's recursive LAPACK (implementeregular LAPACK)
├── test Test codes for BLAS
└── utest Regression test
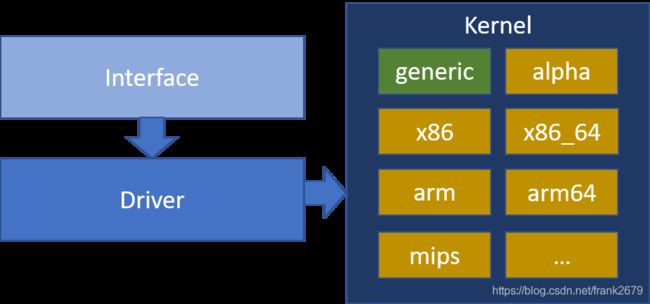
2.2. 软件层次
OpenBLAS 的软件层次比较简单,如上面的源码路径,分为三个层次,分别是 Interface, driver, kernel 层。如下图。
Interface 层的主要作用是根据接口的参数,指定要执行的分支,如我们上图中的例子,走的是 dgemm_nn,即数据是 double 类型,矩阵都不转置。
Driver 层的作用是具体实现,比如 gemm 的 driver 层就是矩阵乘法,由于要实现一个高效率的矩阵乘法,不会只是简单的三层 for 循环就解决了。这一层会做一些任务切分,数据重排,以达到多核并行以及高效利用 cache 来提升 CPU 利用率的目的。
kernel 层是核心运算,这里操作的数据已经都在 cache 上,通过向量化操作,也就是单指令多数据,来高效利用 CPU 的计算能力。
这里的实现要高效,需要使用一些汇编或者是 intrinsic 指令,所以针对不同的 CPU 平台,需要单独实现。
不过通用版本的实现一定会有,以支持暂时还没有优化的平台。
以 gemm 为例,调用关系如下。
interface/gemm.c
│
driver/level3/level3.c
│
gemm assembly kernels at kernel/
具体采用的哪个 kernel 查看预先写好的配置文件 ./kernel/$(ARCH)/KERNEL.$(CPU)。
我这个 case 就是 KERNEL.HASWELL,其中的配置如下:
DGEMMKERNEL = dgemm_kernel_4x8_haswell.S
下面我们详细看一下 OpenBLAS 是如何组织源码的。
2.3. Interface层
刚开始看 OpenBLAS 源码的时候会一脸懵,常常找不到函数定义,就是因为其实现用了大量的宏定义以达到模板编程的效果。
先看最上层源码如下:
interface
├── CMakeFiles
├── lapack
├── netlib # Fortran 实现
├── asum.c
├── bf16to.c
├── cmake_install.cmake
├── CMakeLists.txt
├── copy.c
├── create
├── dot.c
├── dsdot.c
├── gbmv.c
├── geadd.c
├── gemm.c
├── gemv.c
├── ger.c
└── ...
gemm根据数据类型不同分为单精度,双精度,单精度复数,双精度复数的不同版本:sgemm, dgemm, cgemm, zgemm。
但这几种操作基本一致,可以套用一套源码 interface/gemm.c。OpenBLAS 正是这么做的,经过 cmake 后会生成相应的源码。如下:
interface/CMakeFiles/
├── cblas_cgemm.c
├── cblas_dgemm.c
├── cblas_sgemm.c
└── cblas_zgemm.c
cblas_dgemm.c 代码如下,可以看出,cblas_dgemm.c, cblas_sgemm.c 等都是 camke 根据 interface/gemm.c 生成的源码,
#define CBLAS
#define ASMNAME cblas_dgemm
#define ASMFNAME cblas_dgemm_
#define NAME cblas_dgemm_
#define CNAME cblas_dgemm
#define CHAR_NAME "cblas_dgemm_"
#define CHAR_CNAME "cblas_dgemm"
#define DOUBLE
#include "YOUR_PATH/OpenBLAS/interface/gemm.c"
同样由 interface/gemm.c 生成的源码还有 dgemm.c 等,这是因为 OpenBLAS 不光是 CBLAS 库,还要给 LAPACK 调用,所以还提供了另一套接口。
#define ASMNAME dgemm
#define ASMFNAME dgemm_
#define NAME dgemm_
#define CNAME dgemm
#define CHAR_NAME "dgemm_"
#define CHAR_CNAME "dgemm"
#define DOUBLE
#include "YOUR_PATH/OpenBLAS/interface/gemm.c"
现在我们看一下源码 interface/gemm.c 到底怎么选择不同分支的。
没错 CNAME 是函数名,在各自分支中有对应的定义,实际走的分支从全局变量 gemm[] 中提取,又是一堆宏,经过多次定义最终映射到 dgemm_nn.
static int (*gemm[])(blas_arg_t *, BLASLONG *, BLASLONG *, IFLOAT *, IFLOAT *, BLASLONG) = {
#ifndef GEMM3M
GEMM_NN, GEMM_TN, GEMM_RN, GEMM_CN,
GEMM_NT, GEMM_TT, GEMM_RT, GEMM_CT,
GEMM_NR, GEMM_TR, GEMM_RR, GEMM_CR,
GEMM_NC, GEMM_TC, GEMM_RC, GEMM_CC,
#if defined(SMP) && !defined(USE_SIMPLE_THREADED_LEVEL3)
GEMM_THREAD_NN, ...
#endif
#else
GEMM3M_NN, ...
#if defined(SMP) && !defined(USE_SIMPLE_THREADED_LEVEL3)
GEMM3M_THREAD_NN, ...
#endif
#endif
};
void CNAME(enum CBLAS_ORDER order,
enum CBLAS_TRANSPOSE TransA,
enum CBLAS_TRANSPOSE TransB,
blasint m, blasint n, blasint k,
#ifndef COMPLEX
FLOAT alpha,
FLOAT *a, blasint lda,
FLOAT *b, blasint ldb,
FLOAT beta,
FLOAT *c, blasint ldc) {
#else
void *valpha,
void *va, blasint lda,
void *vb, blasint ldb,
void *vbeta,
void *vc, blasint ldc) {
...
#endif
...
(gemm[(transb << 2) | transa])(&args, NULL, NULL, sa, sb, 0);
...
}
#define GEMM_NN DGEMM_NN
#define DGEMM_NN dgemm_nn
从上面的代码可以看出一个不转置地调用 cblas_dgemm 在 interface 层最终调到 dgemm_nn。
2.4. driver层
driver 层才是开始真正干活的层,interface 层已经调用到 dgemm_nn,driver 层按道理应该有该函数的定义。
没错,还是找不到,又是同样的伎俩,需要 cmake 之后才能看到一个 dgemm_nn.c 出现,函数名又一次出现在了宏定义中。如下:
driver/level3
├── CMakeFiles
├── cmake_install.cmake
├── CMakeLists.txt
├── gemm.c
├── gemm_thread_m.c
├── gemm_thread_mn.c
├── gemm_thread_n.c
...
driver/level3/CMakeFiles/
├── ...
├── dgemm_nn.c
├── dgemm_nt.c
├── dgemm_tn.c
├── dgemm_tt.c
├── sgemm_nn.c
├── sgemm_nt.c
├── sgemm_tn.c
├── sgemm_tt.c
...
经过 cmake,会生成一个 dgemm_nn.c, 具体代码如下,跟 interface 层的用法一致,也是复用一套代码,但这里的 gemm.c 是 driver/level3/gemm.c,
#define NN
#define ASMNAME dgemm_nn
#define ASMFNAME dgemm_nn_
#define NAME dgemm_nn_
#define CNAME dgemm_nn
#define CHAR_NAME "dgemm_nn_"
#define CHAR_CNAME "dgemm_nn"
#define DOUBLE
#include "YOUR_PATH/OpenBLAS/driver/level3/gemm.c"
顺藤摸瓜,driver/level3/gemm.c 源码如下,也只是个过路的,继续去找 level3.c。
#ifdef THREADED_LEVEL3
#include "level3_thread.c"
#else
#include "level3.c"
#endif
在看 OpenBLAS 的高级实现之前,我们先看一下最 low 但是好理解的实现
for (m = 0; m < M; m++)
{
for (n = 0; n < N; n++)
{
for (k = 0; k < K; k++)
{
C[m*N + n] += A[m*K + k] * B[k*N + n];
}
}
}
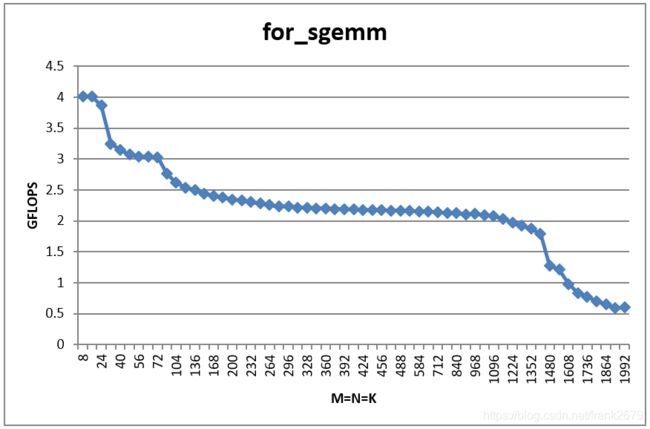
矩阵乘法其实就这么简单,但是如果 M,N,K 很大,会有问题的,如下图,横轴是矩阵的规格,纵轴是实际执行的性能,GFLOPS 表示 1 0 9 / s 10^9/s 109/s 浮点操作。值越高越好。可以看到这个实现真的太弱了。
不过从中可以看到一些端倪,规格越大,我们的性能会变差,原因是 CPU 的三层缓存机制,缓存放不下要计算的数据了,只能到内存中去取,性能自然就下来了。这个情况在 OpenBLAS 的实现中就不存在了。
现在看看 driver/level3/level3.c 这个 gemm 的真正实现,如下,里面的逻辑稍稍复杂,以下是将其中的一些其他宏去掉,并且做了代码对齐。逻辑就清楚很多了。
简单来说就是将 B 矩阵在 N 方向上做切分,切分参数为 GEMM_R,第二层 for 循环在 K 方向上切分, 参数为 GEMM_Q。
最内层先循环有串行的两个循环,第一个循环目的是将切分后的 B 矩阵重排一次,第二个循环时 B 矩阵已经重排好,A 矩阵被切分,切分参数为 GEMM_P,GEMM_P * GEMM_Q 就是根据 L2 cache size 来确定。完了,是不是很简单。
int CNAME(blas_arg_t *args, BLASLONG *range_m, BLASLONG *range_n,
XFLOAT *sa, XFLOAT *sb, BLASLONG dummy){
...
l2size = GEMM_P * GEMM_Q;
// 矩阵乘法的三次切分
for(js = n_from; js < n_to; js += GEMM_R){
min_j = n_to - js;
if (min_j > GEMM_R) min_j = GEMM_R;
for(ls = 0; ls < k; ls += min_l){
min_l = k - ls;
if (min_l >= GEMM_Q * 2) {
min_l = GEMM_Q;
} else {
if (min_l > GEMM_Q) {
min_l = ((min_l / 2 + GEMM_UNROLL_M - 1)/GEMM_UNROLL_M) * GEMM_UNROLL_M;
}
gemm_p = ((l2size / min_l + GEMM_UNROLL_M - 1)/GEMM_UNROLL_M) * GEMM_UNROLL_M;
while (gemm_p * min_l > l2size) gemm_p -= GEMM_UNROLL_M;
}
/* First, we have to move data A to L2 cache */
min_i = m_to - m_from;
l1stride = 1;
if (min_i >= GEMM_P * 2) {
min_i = GEMM_P;
} else {
if (min_i > GEMM_P) {
min_i = ((min_i / 2 + GEMM_UNROLL_M - 1)/GEMM_UNROLL_M) * GEMM_UNROLL_M;
} else {
l1stride = 0;
}
}
ICOPY_OPERATION(min_l, min_i, a, lda, ls, m_from, sa);
for(jjs = js; jjs < js + min_j; jjs += min_jj){
min_jj = min_j + js - jjs;
if (min_jj >= 3*GEMM_UNROLL_N) min_jj = 3*GEMM_UNROLL_N;
else
if (min_jj > GEMM_UNROLL_N) min_jj = GEMM_UNROLL_N;
OCOPY_OPERATION(min_l, min_jj, b, ldb, ls, jjs,
sb + min_l * (jjs - js) * COMPSIZE * l1stride);
KERNEL_OPERATION(min_i, min_jj, min_l, alpha,
sa, sb + min_l * (jjs - js) * COMPSIZE * l1stride, c, ldc, m_from, jjs);
}
for(is = m_from + min_i; is < m_to; is += min_i){
min_i = m_to - is;
if (min_i >= GEMM_P * 2) {
min_i = GEMM_P;
} else {
if (min_i > GEMM_P) {
min_i = ((min_i / 2 + GEMM_UNROLL_M - 1)/GEMM_UNROLL_M) * GEMM_UNROLL_M;
}
}
ICOPY_OPERATION(min_l, min_i, a, lda, ls, is, sa);
KERNEL_OPERATION(min_i, min_j, min_l, alpha, sa, sb, c, ldc, is, js);
} /* end of is */
} /* end of ls */
} /* end of js */
}
宏转换如下,最终调到 dgemm_kernel。
#define KERNEL_OPERATION(M, N, K, ALPHA, SA, SB, C, LDC, X, Y) \
KERNEL_FUNC(M, N, K, ALPHA[0], SA, SB, (FLOAT *)(C) + ((X) + (Y) * LDC) * COMPSIZE, LDC)
#ifndef KERNEL_FUNC
#if defined(NN) || defined(NT) || defined(TN) || defined(TT)
#define KERNEL_FUNC GEMM_KERNEL_N
#endif
#define GEMM_KERNEL_N DGEMM_KERNEL
#define DGEMM_KERNEL dgemm_kernel
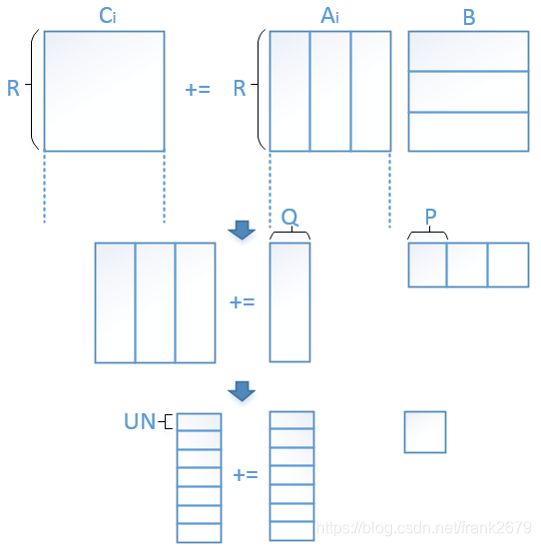
好吧,我知道你现在可能想打我了,先别动手,先看我画个图解释一下,再抽象出伪代码,还不理解再动手不迟。
这张图是我自己当初看 goto 的论文实现的,跟 OpenBLAS 的实现有点反了,可以认为是镜子里的你和镜子外的你,其实都是一个人。
用伪代码描述就清晰很多了,其实就是一个4层 for 循环的循环展开。通过上图中的切分方式,可以将大问题切分成小问题,从而实现加载到 cache 中的数据做尽可能多的运算。
这里的 copy 操作是数据重排的操作,为了保证数据的连续,提升 cache 命中率。
kernel_op 实际上也是一个矩阵乘,它的规格是 CPU 最喜欢的规格。
For m = 0:M, step = R
For k = 0:K, step = Q
For n = 0:N, step = P
Copy_B(Q,P)
For mm = 0:R, step = UN
Copy_A(UN,Q)
kernel_op(A(UN,Q), B(Q,P))
Endfor
Endfor
Endfor
Endfor
上面的方法还有一点可以优化的地方,可以把 A 重排的操作减少掉,伪代码如下,level3.c 中的实现基本就是这种方案。如果还有不清楚的可以去看一下 goto 的论文,或者评论中留言。
For m = 0:M, step = R
For k = 0:K, step = Q
Copy_B(Q,P)
For mm = 0:R, step = UN
Copy_A(UN,Q)
kernel_op(A(UN,Q), B(Q,P))
Endfor
// A(R,Q)经过上一个for已经全部重排完,不用再重排了
For n = 1:N, step = P
Copy_B(Q,P)
Kernel_op(A(R,Q),B(Q,P))
Endfor
Endfor
Endfor
2.5. kernel层
终于到最下面的 kernel 层了,有了上面的框架,kernel 的实现就只能硬干了,没什么投机取巧的地方。
先提供一个 generic 的实现,再对特定的 CPU 做汇编/intrinsic 级别的优化。
这也体现了开源的优势,人多力量大,可以大家一起实现。
kernel/
├── alpha
├── arm
├── arm64
├── generic
├── ia64
├── mips
├── mips64
├── power
├── riscv64
├── setparam-ref.c
├── simd
├── sparc
├── x86
├── x86_64
└── zarch
光 HASWELL 就有多种规格的 kernel 实现:
kernel/x86_64/
├── dgemm_kernel_16x2_haswell.S
├── dgemm_kernel_4x4_haswell.S
└── dgemm_kernel_4x8_haswell.S
具体要使用哪个 kernel 需要在一个文件中提前配置好,如下所示
kernel/x86_64/
├── KERNEL
├── KERNEL.ATOM
├── KERNEL.BARCELONA
├── KERNEL.BOBCAT
├── KERNEL.BULLDOZER
├── KERNEL.COOPERLAKE
├── KERNEL.CORE2
├── KERNEL.DUNNINGTON
├── KERNEL.EXCAVATOR
├── KERNEL.generic
├── KERNEL.HASWELL
├── KERNEL.NANO
├── KERNEL.NEHALEM
├── KERNEL.OPTERON
├── KERNEL.OPTERON_SSE3
├── KERNEL.PENRYN
├── KERNEL.PILEDRIVER
├── KERNEL.PRESCOTT
├── KERNEL.SANDYBRIDGE
├── KERNEL.SKYLAKEX
├── KERNEL.STEAMROLLER
└── KERNEL.ZEN
如出一辙,cmake 后生成的 dgemm_kernel.S 文件如下
kernel/CMakeFiles/dgemm_kernel.S
#define ASMNAME dgemm_kernel // 就是生成的汇编代码的函数名称
#define ASMFNAME dgemm_kernel_
#define NAME dgemm_kernel_
#define CNAME dgemm_kernel
#define CHAR_NAME "dgemm_kernel_"
#define CHAR_CNAME "dgemm_kernel"
#define DOUBLE
#include "YOUR_PATH/OpenBLAS/kernel/x86_64/dgemm_kernel_4x8_haswell.S"
dgemm_kernel_4x8_haswell.S 源码如下
PROLOGUE
PROFCODE
subq $STACKSIZE, %rsp
movq %rbx, (%rsp)
movq %rbp, 8(%rsp)
movq %r12, 16(%rsp)
movq %r13, 24(%rsp)
movq %r14, 32(%rsp)
movq %r15, 40(%rsp)
头文件 common_x86_64.h 中将 PROLOGUE 与 ASMNAME 关联上。
#define PROLOGUE \
.text; \
.align 512; \
.globl REALNAME ;\
.type REALNAME, @function; \
REALNAME:
#define REALNAME ASMNAME
还有一些 C 核心计算源码,采用内嵌汇编代码,下面这个例子是 gemv 的一个核心计算。
static void dgemv_kernel_4x4( BLASLONG n, FLOAT **ap, FLOAT *x, FLOAT *y, FLOAT *alpha)
{
BLASLONG register i = 0;
__asm__ __volatile__
(
"vbroadcastsd (%2), %%ymm12 \n\t" // x0
"vbroadcastsd 8(%2), %%ymm13 \n\t" // x1
"vbroadcastsd 16(%2), %%ymm14 \n\t" // x2
"vbroadcastsd 24(%2), %%ymm15 \n\t" // x3
...
)
}
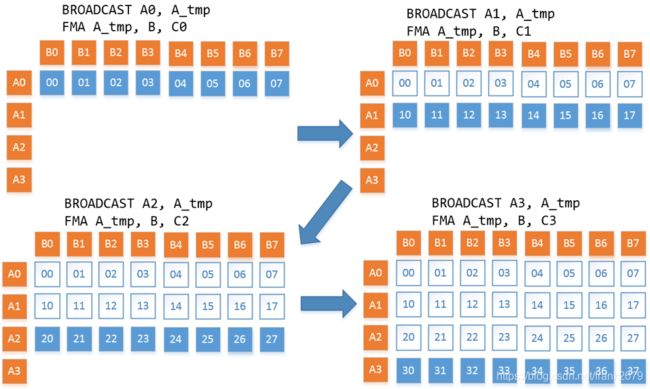
了解了代码框架,我们再来看看 kernel 的原理吧,其实很简单,还是循环展开。
我们前面说 kernel_op 其实也只是矩阵乘,所以也是三层 for 循环。通过展开,让内循环可以使用 SIMD 技术高效计算。
下面的伪代码就是一个 4x8 kernel 的逻辑。
for m = 0:UN, step = 4 (mr)
for n = 0:P, step = 8 (nr)
for k = 0:Q
C(m,n) += A(m,k) * B(k,n);
C(m,n+1) += A(m,k) * B(k,n+1);
C(m,n+2) += A(m,k) * B(k,n+2);
C(m,n+3) += A(m,k) * B(k,n+3);
C(m,n+4) += A(m,k) * B(k,n+4);
...
C(m+1,n) += A(m+1,k) * B(k,n);
...
C(m+3,n+7) += A(m+3,k) * B(k,n+7);
endfor
endfor
endfor
至此,OpenBLAS 中最核心的 level3 实现就基本拿下了。
跑一下最终的版本的性能如下图,分别是单线程和多线程的版本。可以看到随着矩阵size增加性能并不会再降下来了。多线程的并行版本也比单线程的性能提升了6倍多。(我的 CPU 是8核的)
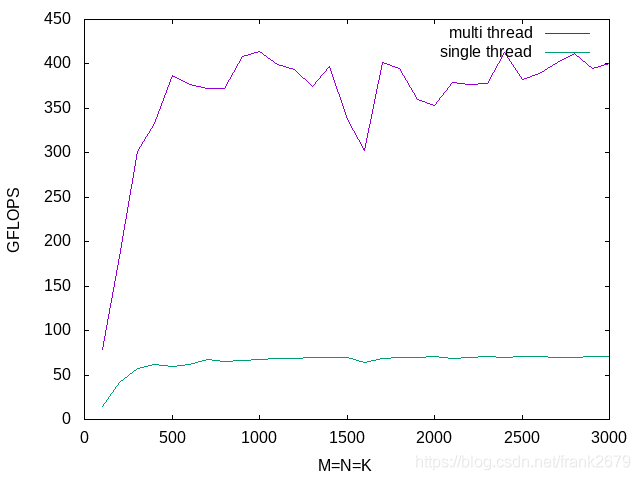
3. 总结
OpenBLAS 是一个比较成功的开源项目,它在多平台兼容性和性能上都有不错的表现。个人分析一方面是其框架还是比较灵活的,方便支持更多平台;另一方面在使用上比较方便,Linux 平台直接 make install 就好。
其实现上对宏的使用不可谓不多,学习了。
但是代码真的不够友善,文档不够完善,源码里面还是有不少小的点无法确认其作用。
后续会对其作为一个完善的开源库,学习其如何维护,包括测试,持续集成等。
4. 附录1 reference
- OpenBLAS official
- OpenBLAS github
- OpenBLAS调用关系
- OpenBLAS源码架构
- BLAS函数定义 netlib
- BLAS函数定义 ustc
- 修改cmake脚本的路径依赖
- xianyi/OpenBLAS介绍与矩阵优化
- Huang, Jianyu, and Robert A Van De Geijn. “BLISlab: A Sandbox for Optimizing GEMM.” arXiv: Mathematical Software (2016).
- Goto, Kazushige, and Robert A Van De Geijn. “Anatomy of high-performance matrix multiplication.” ACM Transactions on Mathematical Software 34.3 (2008).
- Goto, Kazushige, and Robert A Van De Geijn. “High-performance implementation of the level-3 BLAS.” ACM Transactions on Mathematical Software 35.1 (2008).